Neslib.Multiprecision ajoute deux types de points flottants supplémentaires à utiliser avec Delphi. Ceux-ci offrent une précision jusqu'à 4 fois plus grande que celle du Double type.
Neslib.Multiprecision est construit au-dessus du QD 2.3.22 et fonctionne sur:
Les algorithmes utilisés pour ces types ont été développés par David H. Bailey, Yozo Hida et Xiaoye S. Li. Jetez un œil au fichier QD.pdf dans le sous-répertoire C si vous êtes intéressé par les détails.
Pour installer:
> git clone https://github.com/neslib/Neslib.MultiPrecisionCette bibliothèque n'a aucune dépendance sur d'autres bibliothèques. Il n'y a pas non plus de dépendances d'exécution. La bibliothèque C / C ++ QD sous-jacente est liée à l'exécutable à l'aide de fichiers objets ou de bibliothèques statiques.
Cette bibliothèque définit deux types de points flottants supplémentaires:
DoubleDouble : Il s'agit d'un type 128 bits qui a deux fois la précision du Double type.QuadDouble : Il s'agit d'un type de 256 bits qui a quatre fois la précision du Double type. Les deux types ont la même plage que le double type (environ ± 10 308 ) mais une précision beaucoup plus élevée. Par rapport à Single et Double :
| Taper | Exposant Bits | Mantissa Bits | Précision (chiffres décimaux) |
|---|---|---|---|
| Célibataire | 9 | 24 | 7 |
| Double | 12 | 53 | 16 |
| Doublé | 12 | 106 | 32 |
| Quaddouble | 12 | 212 | 64 |
Les noms
DoubleDoubleetQuadDoubleproviennent de la bibliothèque QD sous-jacente. J'ai envisagé à la place de nommer cesFloat128etFloat256, mais il existe déjà des spécifications officielles de l'IEEE pour de tels types (matériels). Et comme ceux-ci ne sont pas compatibles avecDoubleDoubleetQuadDouble, je ne voulais pas ajouter de confusion.
La bibliothèque QD sous-jacente n'utilise pas d'émulation pour les calculs. Au lieu de cela, il utilise les capacités existantes à virgule flottante du CPU pour utiliser 2 ou 4 Double valeurs pour augmenter la précision. En conséquence, ces types sont beaucoup plus rapides que les autres bibliothèques mathématiques arbitraires / à haute précision en utilisant la même précision. De plus, par opposition à de nombreuses autres bibliothèques, ces types ne nécessitent pas d'allocations de mémoire dynamique, ce qui aide encore les performances et réduit également la fragmentation de la mémoire.
Les types DoubleDouble et QuadDouble peuvent être utilisés de la même manière que le Double type. Ils prennent en charge les opérateurs habituels ( + , - , * , / , = , <> , < , <= , > et >= ) ainsi que la plupart des méthodes disponibles pour les aides records pour le Double type ( IsNan , IsInfinity , IsNegativeInfinity , IsPositiveInfinity , ToString , Parse et TryParse ). Il existe des méthodes et des opérateurs à convertir vers et depuis Double , DoubleDouble , QuadDouble et String .
Étant donné que le langage Delphi ne vous permet pas d'entrer des littéraux à point flottant de haute précision dans le code source, la valeur d'une variable DoubleDouble ou QuadDouble doit être initialisée d'une autre manière. Il existe diverses options (en supposant que DD est de type DoubleDouble ici):
Init . Par exemple, DD.Init(1.23); Pour initialiser un DoubleDouble par un Double .DD := DoubleDouble(1.23); .DD := DoubleDouble.Pi; .DD := '3.1415926535897932384626433832795'; .Je n'ai pas ajouté d'opérateurs implicites , tels que
DD := 1.23;, car ceux-ci peuvent conduire à des conversions involontaires qui ont un impact sur les performances.
Il est important que vous appeliez MultiPrecisionInit avant d' effectuer des calculs DoubleDouble / QuadDouble . Cela prépare le FPU / CPU pour les mathématiques de haute précision. Vous pouvez utiliser MultiPrecisionReset pour restaurer le FPU / CPU à son état précédent.
La configuration par défaut de la bibliothèque convient à la plupart des applications. Cette configuration sacrifie un peu de précision pour une vitesse accrue. Si la précision est plus importante que la vitesse à vos fins, vous pouvez compiler la bibliothèque avec la définition MP_ACCURATE . Cela rendra de nombreux calculs un peu plus lents mais plus précis.
La bibliothèque QD sous-jacente (et donc cette bibliothèque) prend en charge une variété de fonctions mathématiques courantes. De plus, la bibliothèque Neslib.Multiprecision ajoute de nombreux équivalents de fonctions trouvées dans les unités System.SYSUTILS et System.math.
| Nom | Description |
|---|---|
| Strtodoubledouble, stroquaddouble, Strtodoubledoubledf, stroquaddoubledf, Trystrtofloat | Convertir à partir de la chaîne |
| FloattoStr, FloattoStrf | Convertir en chaîne |
| Inverse | Calculer réciproque |
| Remorqueur | Calculez le reste, en arrondissant le plus proche |
| Divrem | Calculer le résultat de la division, y compris le reste |
| FMOD | Calculez le reste, arrondi vers zéro |
| SQRT, SQR | Racine carrée et carrée |
| Trunc, plancher, plaque, rond | Diverses méthodes d'arrondi |
| Abs | Valeur absolue |
| Min, max | Renter la valeur minimale ou maximale |
| Inrange, Sureurange | Comparez avec la gamme |
| Même valeur | Vérification approximative de l'égalité |
| Power, intpower, nroot, ldexp, exp | Fonctions exponentielles |
| LN, LNXP1, LOG2, LOG10, LONG | Fonctions logarithmiques |
| Péché, cos, sincos, tan | Fonctions trigonométriques |
| Arcsin, Arccos, Arctan, Arctan2 | Fonctions trigonométriques inverses |
| Sinh, Cosh, Sincosh, Tanh | Fonctions hyperboliques |
| Arcsinh, Arccosh, Arctanh | Fonctions hyperboliques inverses |
| Cotan, Cot, sécant, sec, Cosécant, CSC | Fonctions trigonométriques réciproques |
| Coth, SECH, CSCH | Fonctions hyperboliques réciproques |
| Arccot, arcsec, arccscs | Fonctions trigonométriques inverses réciproques |
| Arccoth, arcsech, arccsch | Fonctions hyperboliques inverses réciproques |
| Radtodeg, radtograd, radtocycle | Se convertir de radians |
| Degtorad, degtograd, degtocycle | Se convertir à partir de degrés |
| Gradtorad, gradtodeg, gradtocycle | Convertir des diplômés |
| Cycletorad, cycletodeg, cycletograd | Convertir des cycles |
Une façon amusante de démontrer les mathématiques de haute précision est de calculer le fractale Mandelbrot. Lorsque vous zoomez sur la fractale, vous avez besoin de plus en plus de précision. Le sous-répertoire des échantillons contient une application FiremonKey qui génère la fractale Mandelbrot à 4 niveaux de précision ( Single , Double , DoubleDouble et QuadDouble ).
L'image suivante montre une minuscule section de la fractale en utilisant un grossissement d'un quadrillion (10 15 , alias un billard en Europe) et Double précision:
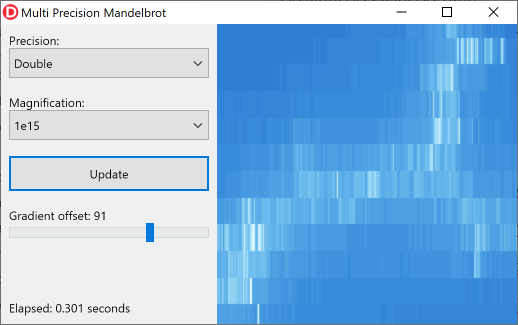
Vous pouvez clairement voir que le Double type ne fournit pas suffisamment de précision à ce niveau d'agrandissement. Le type DoubleDouble offre cependant plus que suffisamment de précision:
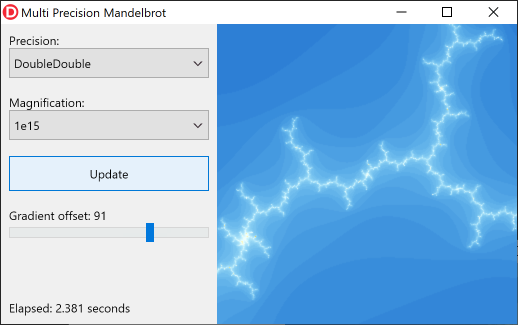
Ce n'est que lorsque vous atteignez un niveau d'agrandissement de 10 31 , que vous devez passer à QuadDouble .
Il y a plus à Neslib.Multiprecision que celle décrite ci-dessus. Pour plus de détails, vous pouvez consulter le fichier source Neslib.MultiPrecision.pas bien documenté. Des échantillons d'utilisation supplémentaires peuvent être trouvés dans le sous-répertoire unittests et l'application de l'échantillon Mandelbrot.
Si vous êtes intéressé par les détails techniques et les algorithmes utilisés pour ces types, vous pouvez jeter un œil au fichier QD.pdf dans le sous-répertoire C.
Comme dit, cette bibliothèque est construite au-dessus de la bibliothèque QD. Il s'agit d'une bibliothèque C / C ++ liée à votre exécutable Delphi à l'aide de fichiers objets ou de bibliothèques statiques. Si jamais vous avez besoin ou souhaitez créer vous-même ces fichiers d'objets et ces bibliothèques statiques, consultez le fichier readme.txt dans le sous-répertoire C pour les instructions.
Neslib.Multiprecision est sous licence sous la licence BSD simplifiée. Voir Licence.txt pour plus de détails.
La bibliothèque QD sous-jacente est sous licence BSD-LBNL. Voir le document bsd-lbnl-license.doc dans le sous-répertoire C pour plus de détails.