Neslib.multipRecision fügt zwei zusätzliche Gleitkomma-Typen für die Verwendung mit Delphi hinzu. Diese bieten eine Präzision, die bis zu 4 -mal größer ist als die des Double .
Neslib.multipRecision wird auf dem QD 2.3.22 aufgebaut und funktioniert an:
Die für diese Typen verwendeten Algorithmen wurden von David H. Bailey, Yozo Hida und Xiaoye S. Li entwickelt. Schauen Sie sich die Datei QD.PDF im C -Unterverzeichnis an, wenn Sie an den Details interessiert sind.
Zu installieren:
> git clone https://github.com/neslib/Neslib.MultiPrecisionDiese Bibliothek hat keine Abhängigkeiten von anderen Bibliotheken. Es gibt auch keine Laufzeitabhängigkeiten. Die zugrunde liegende C/C ++ - QD -Bibliothek wird mithilfe von Objektdateien oder statischen Bibliotheken in die ausführbare Datei verknüpft.
Diese Bibliothek definiert zwei zusätzliche Gleitkomma-Typen:
DoubleDouble : Dies ist ein 128-Bit-Typ, der die doppelte Genauigkeit des Double hat.QuadDouble : Dies ist ein 256-Bit-Typ, der die vierfache Genauigkeit des Double hat. Beide Typen haben den gleichen Bereich wie der Doppeltyp (ca. ± 10 308 ), aber viel höhere Präzision. Im Vergleich zu Single und Double :
| Typ | Exponent Bits | Mantisse Bits | Präzision (Dezimalstellen) |
|---|---|---|---|
| Einzel | 9 | 24 | 7 |
| Doppelt | 12 | 53 | 16 |
| Verdoppelt | 12 | 106 | 32 |
| Quaddouble | 12 | 212 | 64 |
Die Namen
DoubleDoubleundQuadDoublestammen aus der zugrunde liegenden QD -Bibliothek. Ich habe stattdessen überlegt, dieseFloat128undFloat256zu benennen, aber es gibt bereits offizielle IEEE -Spezifikationen für solche (Hardware-) Typen. Und da diese nicht mitDoubleDoubleundQuadDoublekompatibel sind, wollte ich nicht Verwirrung hinzufügen.
Die zugrunde liegende QD -Bibliothek verwendet keine Emulation für Berechnungen. Stattdessen verwendet es die vorhandenen Floating-Punkt-Funktionen der CPU, um entweder 2 oder 4 Double zu verwenden, um die Genauigkeit zu erhöhen. Infolgedessen sind diese Typen viel schneller als andere willkürliche/hohe Präzisionsmathematikbibliotheken mit derselben Genauigkeit. Im Gegensatz zu vielen anderen Bibliotheken erfordern diese Typen keine dynamischen Speicherzuweisungen, was die Leistung weiter hilft und auch die Gedächtnisfragmentierung verringert.
Die DoubleDouble und QuadDouble -Typen können genauso verwendet werden wie der Double . Sie unterstützen die üblichen Operatoren ( + , - , * , / , = , <> , < , <= , > und >= ) sowie die meisten Methoden, die für die Datensatzhelfer für den Double ( IsNan , IsInfinity , IsNegativeInfinity , IsPositiveInfinity , ToString , Parse ) verfügbar TryParse . Es gibt Methoden und Operatoren, die zum und von Double , DoubleDouble , QuadDouble und String konvertieren können.
Da die Delphi-Sprache es Ihnen nicht erlaubt, in den Quellcode hochpräzisen schwimmende Punktliterale einzugeben, muss der Wert einer DoubleDouble oder QuadDouble Variablen auf andere Weise initialisiert werden. Es gibt verschiedene Optionen (vorausgesetzt, DD ist hier DoubleDouble ):
Init -Überlastungen. Zum Beispiel DD.Init(1.23); Ein DoubleDouble aus einem Double initialisieren.DD := DoubleDouble(1.23); .DD := DoubleDouble.Pi; .DD := '3.1415926535897932384626433832795'; .Ich habe implizite Operatoren wie
DD := 1.23;da diese zu unbeabsichtigten Conversions führen können, die die Leistung beeinflussen.
Es ist wichtig, dass Sie MultiPrecisionInit nennen, bevor Sie DoubleDouble / QuadDouble -Berechnungen durchführen. Dies bereitet die FPU/CPU für die Mathematik mit hoher Präzision vor. Sie können MultiPrecisionReset verwenden, um die FPU/CPU in ihren vorherigen Zustand wiederherzustellen.
Die Standardkonfiguration der Bibliothek ist für die meisten Anwendungen geeignet. Diese Konfiguration opfert ein wenig Genauigkeit für eine erhöhte Geschwindigkeit. Wenn die Genauigkeit für Ihre Zwecke wichtiger als Geschwindigkeit ist, können Sie die Bibliothek mit dem Definieren MP_ACCURATE kompilieren. Dies wird viele Berechnungen etwas langsamer, aber genauer machen.
Die zugrunde liegende QD -Bibliothek (und damit diese Bibliothek) unterstützt eine Vielzahl gemeinsamer mathematischer Funktionen. Darüber hinaus fügt die Bibliothek von Neslib.MultipRecision zahlreiche Äquivalente von Funktionen hinzu, die im System enthalten sind.
| Name | Beschreibung |
|---|---|
| Strtodoubledouble, Strtoquaddouble, Strtodoubledoulbledeff, Strtoquaddoubledef, Trystrtofloat | Von String konvertieren |
| Floattostr, Floattostrf | Zu String konvertieren |
| Umgekehrt | Rechnen Sie gegenseitig |
| Rem | Berechnen Sie den Rest, runden Sie sie auf die nächste ab |
| Divrem | Berechnen Sie das Ergebnis der Division, einschließlich Rest |
| Fmod | Berechnen Sie den Rest, auf Null gerundet |
| SQRT, SQR | Quadratwurzel und Quadrat |
| Kreisel, Boden, Ceil, rund | Verschiedene Rundungsmethoden |
| ABS | Absolutwert |
| Min, Max | Mindest- oder Maximalwert zurückgeben |
| Inrange, Enserange | Vergleiche mit Reichweite |
| Gleicher Wert | Ungefähre Gleichstellungsprüfung |
| Power, Intpower, Nroot, ldexp, exp | Exponentialfunktionen |
| Ln, lnxp1, log2, log10, logn | Logarithmische Funktionen |
| Sünde, Cos, Sincos, Bräune | Trigonometrische Funktionen |
| Arcsin, Arccos, Arctan, Arctan2 | Inverse trigonometrische Funktionen |
| Sinh, Cosh, Sincosh, Tanh | Hyperbolische Funktionen |
| Arcsinh, Arccosh, Arctanh | Inverse hyperbolische Funktionen |
| Cotan, Cot, Secant, Sec, Cosecant, CSC | Wechselseitige trigonometrische Funktionen |
| COTH, SECH, CSCH | Wechselseitige hyperbolische Funktionen |
| Arccot, Arcsec, Arccsc | Wechselseitige inverse trigonometrische Funktionen |
| Arccoth, Arcsech, Arccsch | Wechselseitige inverse hyperbolische Funktionen |
| Radtodeg, Radtograd, Radtocycle | Von Radians konvertieren |
| Degtorad, degtograd, degtocycle | Aus Grad konvertieren |
| Gradtorad, GradTodeg, Gradtocycle | Von Absolventen konvertieren |
| Cycletorad, Cycletodeg, Cycletograd | Aus Zyklen konvertieren |
Ein unterhaltsamer Weg, um die Mathematik mit hoher Präzision zu demonstrieren, besteht darin, den Mandelbrot-Fraktal zu berechnen. Wenn Sie in den Fraktal vergrößern, brauchen Sie immer mehr Präzision. Das Proben -Unterverzeichnis enthält eine Fironemonkey -Anwendung, die das Mandelbrot -Fraktal bei 4 Präzisionsniveaus erzeugt ( Single , Double , DoubleDouble und QuadDouble ).
Das folgende Bild zeigt einen winzigen Abschnitt des Fraktals unter Verwendung einer Vergrößerung von einem Quadrang (10 15 , auch bekannt als ein Billard in Europa) und Double Präzision:
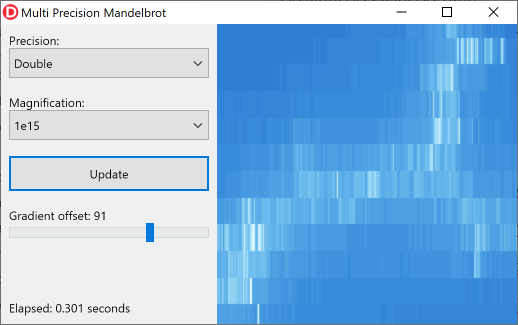
Sie können deutlich sehen, dass der Double auf dieser Vergrößerungsstufe nicht genügend Präzision bietet. Der DoubleDouble -Typ bietet jedoch mehr als genügend Präzision:
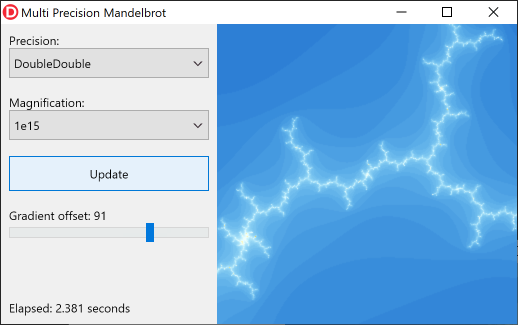
Erst wenn Sie eine Vergrößerungsstufe von 10 31 erreichen, müssen Sie auf QuadDouble wechseln.
Neslib hat mehr als oben beschrieben. Weitere Informationen finden Sie in der gut dokumentierten Quelldatei Neslib.MultiPrecision.pas . Zusätzliche Nutzungsproben finden Sie im Unterabditionorium der Unittests und in der Mandelbrot -Stichprobenanwendung.
Wenn Sie an den technischen Details und Algorithmen interessiert sind, die für diese Typen verwendet werden, können Sie sich die QD.PDF -Datei im C -Unterverzeichnis ansehen.
Wie gesagt, diese Bibliothek ist auf der QD -Bibliothek aufgebaut. Dies ist eine C/C ++ - Bibliothek, die mithilfe von Objektdateien oder statischen Bibliotheken in Ihre ausführbare Delphi -ausführbare Datei verknüpft ist. Wenn Sie diese Objektdateien und statischen Bibliotheken selbst benötigen oder selbst erstellen möchten, lesen Sie die LEADME.TXT -Datei im C -Unterverzeichnis C, um Anweisungen zu erhalten.
Neslib.multipRecision ist unter der vereinfachten BSD -Lizenz lizenziert. Einzelheiten siehe Lizenz.txt.
Die zugrunde liegende QD-Bibliothek ist unter der BSD-LBNL-Lizenz lizenziert. Weitere Informationen finden Sie im Dokument BSD-LBNL-LICENSE.DOC im C-Unterverzeichnis.