Neslib.multiprecision agrega dos tipos de puntos flotantes adicionales para usar con Delphi. Estos ofrecen una precisión que es hasta 4 veces más grande que la del tipo Double .
Neslib.multiprecision se basa en la parte superior del QD 2.3.22 y funciona en:
Los algoritmos utilizados para estos tipos fueron desarrollados por David H. Bailey, Yozo Hida y Xiaoye S. Li. Eche un vistazo al archivo QD.PDF en el subdirectorio C si está interesado en los detalles.
Para instalar:
> git clone https://github.com/neslib/Neslib.MultiPrecisionEsta biblioteca no tiene dependencias en otras bibliotecas. Tampoco hay dependencias de tiempo de ejecución. La biblioteca C/C ++ QD subyacente está vinculada al ejecutable usando archivos de objetos o bibliotecas estáticas.
Esta biblioteca define dos tipos adicionales de punto flotante:
DoubleDouble : Este es un tipo de 128 bits que tiene el doble de precisión del tipo Double .QuadDouble : este es un tipo de 256 bits que tiene cuatro veces la precisión del tipo Double . Ambos tipos tienen el mismo rango que el tipo doble (aproximadamente ± 10 308 ) pero una precisión mucho más alta. En comparación con Single y Double :
| Tipo | Exponente Brocas | Mantissa Brocas | Precisión (dígitos decimales) |
|---|---|---|---|
| Soltero | 9 | 24 | 7 |
| Doble | 12 | 53 | 16 |
| Doubleubouble | 12 | 106 | 32 |
| Cuádruple | 12 | 212 | 64 |
Los nombres
DoubleDoubleyQuadDoubleprovienen de la biblioteca QD subyacente. En su lugar, consideré nombrar estosFloat128yFloat256, pero ya hay especificaciones oficiales de IEEE para tales tipos (de hardware). Y dado que estos no son compatibles conDoubleDoubleyQuadDouble, no quería agregar confusión.
La biblioteca QD subyacente no utiliza la emulación para los cálculos. En su lugar, utiliza las capacidades existentes de punto flotante de la CPU para usar 2 o 4 valores Double para aumentar la precisión. Como resultado, estos tipos son mucho más rápidos que otras bibliotecas de matemáticas arbitrarias/de alta precisión que usan la misma precisión. Además, a diferencia de muchas otras bibliotecas, estos tipos no requieren asignaciones de memoria dinámica, lo que aún ayuda al rendimiento y también reduce la fragmentación de la memoria.
Los tipos DoubleDouble y QuadDouble se pueden usar de la misma manera que el tipo Double . Apoyan a los operadores habituales ( + , - , * , / , = , <> , < , <= , > y >= ), así como la mayoría de los métodos disponibles para los ayudantes de registro para el tipo Double ( IsNan , IsInfinity , IsNegativeInfinity , IsPositiveInfinity , ToString , Parse y TryParse ). Hay métodos y operadores para convertir hacia y desde Double , DoubleDouble , QuadDouble y String .
Dado que el lenguaje Delphi no le permite ingresar literales de punto flotante de alta precisión en el código fuente, el valor de una variable DoubleDouble o QuadDouble debe inicializarse de alguna otra manera. Hay varias opciones (suponiendo que DD sea de tipo DoubleDouble aquí):
Init . Por ejemplo, DD.Init(1.23); Para inicializar un DoubleDouble de un Double .DD := DoubleDouble(1.23); .DD := DoubleDouble.Pi; .DD := '3.1415926535897932384626433832795'; .No agregué operadores implícitos , como
DD := 1.23;, dado que pueden conducir a conversiones involuntarias que afectan el rendimiento.
Es importante que llame MultiPrecisionInit antes de realizar cualquier cálculo DoubleDouble / QuadDouble . Esto prepara la FPU/CPU para matemáticas de alta precisión. Puede usar MultiPrecisionReset para restaurar la FPU/CPU a su estado anterior.
La configuración predeterminada de la biblioteca es adecuada para la mayoría de las aplicaciones. Esta configuración sacrifica un poco de precisión para una mayor velocidad. Si la precisión es más importante que la velocidad para sus propósitos, entonces puede compilar la biblioteca con el MP_ACCURATE Define. Esto hará que muchos cálculos sean un poco más lentos pero más precisos.
La biblioteca QD subyacente (y, por lo tanto, esta biblioteca) admite una variedad de funciones matemáticas comunes. Además, la biblioteca Neslib.Multiprecision agrega numerosos equivalentes de funciones encontradas en el sistema.
| Nombre | Descripción |
|---|---|
| Strtodoubleubouble, strtoquaddouble, StrtodoubleBllefef, strtoquaddoublefef, Trystrtofloat | Convertir de String |
| Floattostr, FloatTostrf | Convertir a cadena |
| Inverso | Calcular recíproca |
| Movimiento rápido del ojo | Calcular el resto, redondeo al más cercano |
| Divrem | Calcule el resultado de la división, incluido el resto |
| Fmod | Calcule el resto, redondeado hacia cero |
| Sqrt, sqr | Raíz cuadrada y cuadrado |
| Trunc, piso, techo, redondo | Varios métodos de redondeo |
| Abdominales | Valor absoluto |
| Min, Max | Devolver un valor mínimo o máximo |
| Ingrange, Assurerange | Comparar contra el rango |
| Mismo valor | Verificación de igualdad aproximada |
| Potencia, intpower, nroot, ldexp, exp | Funciones exponenciales |
| LN, LNXP1, LOG2, LOG10, LOGN | Funciones logarítmicas |
| Pecado, cos, sincos, bronceado | Funciones trigonométricas |
| Arcsin, Arccos, Arctan, Arctan2 | Funciones trigonométricas inversas |
| Sinh, Cosh, Sincosh, Tanh | Funciones hiperbólicas |
| Arcsinh, ArcCosh, Arctanh | Funciones hiperbólicas inversas |
| Cotan, Cot, Secant, Sec, Cosecant, CSC | Funciones trigonométricas recíprocas |
| Coth, SECH, CSCH | Funciones hiperbólicas recíprocas |
| Arccot, ArcSec, ArccSC | Funciones trigonométricas inversas recíprocas |
| Arccoth, Arcsech, Arccsch | Funciones hiperbólicas inversas recíprocas |
| Radtodeg, Radtograd, Radtocycle | Convertir de radianes |
| Degtorad, Degtograd, Degtocycle | Convertir de grados |
| Gradtorad, Gradtodeg, Gradtocycle | Convertir de los graduados |
| Cycletorad, Cycletodegg, Cycletograd | Convertir de ciclos |
Una forma divertida de demostrar matemáticas de alta precisión es calcular el fractal Mandelbrot. A medida que se acerca al fractal, necesita más y más precisión. El subdirectorio de muestras contiene una aplicación Firememonkey que genera el fractal de Mandelbrot a 4 niveles de precisión ( Single , Double , DoubleDouble y QuadDouble ).
La siguiente imagen muestra una pequeña sección de la fractal utilizando un aumento de un cuadrillón (10 15 , también conocido como un billar en Europa) y Double precisión:
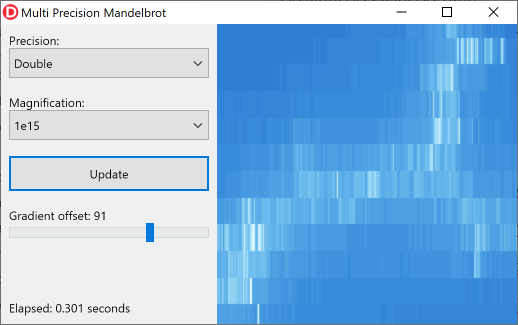
Puede ver claramente que el tipo Double no proporciona suficiente precisión en este nivel de aumento. Sin embargo, el tipo DoubleDouble ofrece precisión más que suficiente:
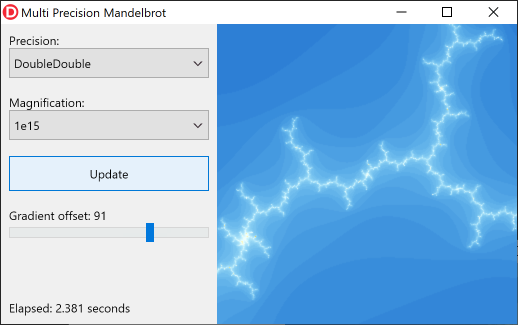
No es hasta que alcanza un nivel de aumento de 10 31 , que debe cambiar a QuadDouble .
Hay más en neslib.multiprecision que el descrito anteriormente. Para obtener más detalles, puede ver el archivo de origen Neslib.MultiPrecision.pas bien documentado. Se pueden encontrar muestras de uso adicionales en el subdirectorio Unittests y la aplicación de muestra MandelBrot.
Si está interesado en los detalles técnicos y los algoritmos utilizados para estos tipos, puede echar un vistazo al archivo QD.PDF en el subdirectorio C.
Como se dice, esta biblioteca se construye en la parte superior de la biblioteca QD. Esta es una biblioteca C/C ++ que está vinculada a su ejecutable de Delphi usando archivos de objetos o bibliotecas estáticas. Si alguna vez necesita o desea construir estos archivos de objetos y bibliotecas estáticas usted mismo, eche un vistazo al archivo ReadMe.txt en el subdirectorio C para obtener instrucciones.
Neslib.multiprecision tiene licencia bajo la licencia BSD simplificada. Consulte License.txt para más detalles.
La biblioteca QD subyacente tiene licencia bajo la licencia BSD-LBNL. Consulte el documento BSD-LBNL-license.doc en el subdirectorio C para más detalles.