Главная страница>Исходный код JSP>Другие категории
Скачать

Оглавление

  • Что такое PEM?
  • Обзор
  • Установка
  • Использование
    • Исполняемый файл
    • Библиотека
    • Телеграмма бот
    • Попробуйте Opem в своем браузере!
    • Матлаб
  • Проблемы и отчеты об ошибках
  • Вклад
  • Выходы
  • Спасибо
  • Ссылка
  • Цитировать
  • Авторы
  • Лицензия
  • Покажите свою поддержку
  • Изменение
  • Нормы поведения

Обзор

Моделирование и моделирование протон-обмена топливных элементов мембран (PEMFC) могут работать в качестве мощного инструмента в исследованиях и разработки источников возобновляемых источников энергии. Инструмент моделирования PEMFC с открытым исходным кодом (OPEM) представляет собой инструмент моделирования для оценки производительности протонных обмена топливных элементов. Этот пакет представляет собой комбинацию моделей (статических/динамических), которые предсказывают оптимальные рабочие параметры PEMFC. OPEM содержал общие модели, которые будут принимать в качестве входных данных, не только значения рабочих переменных, таких как анод и катодный подача газа, давление и состав, температуру ячейки и плотность тока, но и параметры ячейки, включая активную площадь и толщину мембраны. Кроме того, некоторые из различных моделей PEMFC, которые были предложены в OPEM, просто сосредоточены на одном конкретном стеке FC, а некоторые другие принимают во внимание часть или все вспомогательные организации, такие как реформаторы. OPEM - это платформа для совместной разработки моделей PEMFC.

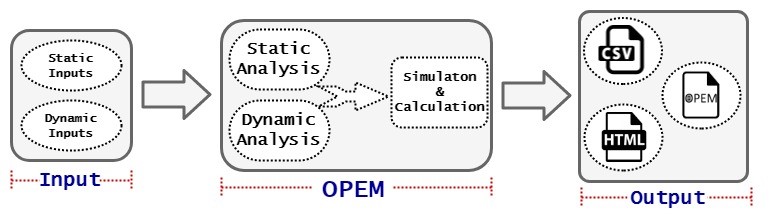
Рис. Блок -диаграмма опемо

Открытый центр
Счетчик PYPI
Звезды GitHub
Ветвь владелец развивать
CI
Качество кода

Использование

Исполняемый файл

  • Откройте CMD (Windows) или Terminal (UNIX)

  • Запустить opem или python -m opem (или запустить OPEM.exe )

  • Введите параметры ячейки PEM (или запустить стандартные векторы тестирования)

    1. Статическая модель Amphlett

      Вход Описание Единица
      Т Температура работы ячейки K
      PH2 Частичное давление банкомат
      PO2 Частичное давление банкомат
      I-Start Ячейка рабочего тока начальной точки А
      i-step Шаг тока рабочих клеток А
      i-stop Конечная точка операционного тока ячейки А
      А Активная площадь CM^2
      л Толщина мембраны см
      лямбда Регулируемый параметр со значением мин 14 и максимальным значением 23 -
      R (*Необязательно) R-электронная ом
      Jmax Максимальная плотность тока A/(cm^2)
      Не Количество отдельных клеток -
       * Для получения дополнительной информации об этой модели посетите здесь

    2. Larminie-Dicks Static Model

      Вход Описание Единица
      E0 Обратимое топливное ячейки без напряжения потерь V.
      А Наклон линии Тафеля V.
      Т Температура работы ячейки K
      I-Start Ячейка рабочего тока начальной точки А
      i-step Шаг тока рабочих клеток А
      i-stop Конечная точка операционного тока ячейки А
      в Внутренний ток А
      I_0 Обмен ток, при котором перенаселение начинает двигаться от нуля А
      i_l Ограничивающий ток А
      Rm Мембрана и сопротивление контактов ом
      Не Количество отдельных клеток -
       * Для получения дополнительной информации об этой модели посетите здесь

    3. Статическая модель Camberline-Kim

      Вход Описание Единица
      E0 Открыть напряжение цепи V.
      беременный Параметр Тафеля для восстановления кислорода V.
      Ведущий Сопротивление Ohm.cm^2
      I-Start Ячейка рабочего тока начальной точки А
      i-step Шаг тока рабочих клеток А
      i-stop Конечная точка операционного тока ячейки А
      А Активная площадь CM^2
      м Параметры диффузии V.
      не Параметры диффузии (A^-1) (cm^2)
      Не Количество отдельных клеток -
       * Для получения дополнительной информации об этой модели посетите здесь

    4. Динамическая модель Padulles I

      Вход Описание Единица
      E0 Нет напряжения нагрузки V.
      Т Температура топливных элементов K
      KH2 Постоянный водород kmol.s^(-1) .atm^(-1)
      Ko2 Кислородный клапан постоянный kmol.s^(-1) .atm^(-1)
      Th2 Время водорода постоянно с
      до 2 Время кислорода постоянно с
      Беременный Постоянная активация напряжения V.
      В Параметр постоянной активации A^(-1)
      Прозрачный Внутреннее сопротивление топливного элемента ом
      родовой Коэффициент потока водорода-кислорода -
      QH2 Молярный поток водорода Kmol/s
      Не Количество ячеек -
      I-Start Ячейка рабочего тока начальной точки А
      i-step Шаг тока рабочих клеток А
      i-stop Конечная точка операционного тока ячейки А
       * Для получения дополнительной информации об этой модели посетите здесь

    5. Динамическая модель Padulles Model II

      Вход Описание Единица
      E0 Нет напряжения нагрузки V.
      Т Температура топливных элементов K
      KH2 Постоянный водород kmol.s^(-1) .atm^(-1)
      KH2O Постоянный водяной клапан kmol.s^(-1) .atm^(-1)
      Ko2 Кислородный клапан постоянный kmol.s^(-1) .atm^(-1)
      Th2 Время водорода постоянно с
      th2o Время воды постоянно с
      до 2 Время кислорода постоянно с
      Беременный Постоянная активация напряжения V.
      В Параметр постоянной активации A^(-1)
      Прозрачный Внутреннее сопротивление топливного элемента ом
      родовой Коэффициент потока водорода-кислорода -
      QH2 Молярный поток водорода Kmol/s
      Не Количество ячеек -
      I-Start Ячейка рабочего тока начальной точки А
      i-step Шаг тока рабочих клеток А
      i-stop Конечная точка операционного тока ячейки А
       * Для получения дополнительной информации об этой модели посетите здесь

    6. Динамическая модель Padulles-Hauer

      Вход Описание Единица
      E0 Нет напряжения нагрузки V.
      Т Температура топливных элементов K
      KH2 Постоянный водород kmol.s^(-1) .atm^(-1)
      KH2O Постоянный водяной клапан kmol.s^(-1) .atm^(-1)
      Ko2 Кислородный клапан постоянный kmol.s^(-1) .atm^(-1)
      Th2 Время водорода постоянно с
      th2o Время воды постоянно с
      до 2 Время кислорода постоянно с
      T1 Реформаторский время постоянно с
      T2 Реформаторский время постоянно с
      Беременный Постоянная активация напряжения V.
      В Параметр постоянной активации A^(-1)
      резюме Коэффициент преобразования -
      Прозрачный Внутреннее сопротивление топливного элемента ом
      родовой Коэффициент потока водорода-кислорода -
      Qmethanol Молярный поток метанола Kmol/s
      Не Количество ячеек -
      I-Start Ячейка рабочего тока начальной точки А
      i-step Шаг тока рабочих клеток А
      i-stop Конечная точка операционного тока ячейки А
       * Для получения дополнительной информации об этой модели посетите здесь

    7. Динамическая модель Padulles-Amphlett

      Вход Описание Единица
      E0 Нет напряжения нагрузки V.
      Т Температура топливных элементов K
      KH2 Постоянный водород kmol.s^(-1) .atm^(-1)
      KH2O Постоянный водяной клапан kmol.s^(-1) .atm^(-1)
      Ko2 Кислородный клапан постоянный kmol.s^(-1) .atm^(-1)
      Th2 Время водорода постоянно с
      th2o Время воды постоянно с
      до 2 Время кислорода постоянно с
      T1 Реформаторский время постоянно с
      T2 Реформаторский время постоянно с
      А Активная площадь CM^2
      л Толщина мембраны см
      лямбда Регулируемый параметр со значением мин 14 и максимальным значением 23 -
      R (*Необязательно) R-электронная ом
      Jmax Максимальная плотность тока A/(cm^2)
      резюме Коэффициент преобразования -
      родовой Коэффициент потока водорода-кислорода -
      Qmethanol Молярный поток метанола Kmol/s
      Не Количество ячеек -
      I-Start Ячейка рабочего тока начальной точки А
      i-step Шаг тока рабочих клеток А
      i-stop Конечная точка операционного тока ячейки А
       * Для получения дополнительной информации об этой модели посетите здесь

    8. Динамическая модель чакраборти

      Вход Описание Единица
      E0 Нет напряжения нагрузки V.
      Т Температура работы ячейки K
      KH2 Постоянный водород kmol.s^(-1) .atm^(-1)
      KH2O Постоянный водяной клапан kmol.s^(-1) .atm^(-1)
      Ko2 Кислородный клапан постоянный kmol.s^(-1) .atm^(-1)
      родовой Коэффициент потока водорода-кислорода -
      Прозрачный Внутреннее сопротивление топливного элемента ом
      Не Количество ячеек -
      u Коэффициент использования топлива -
      I-Start Ячейка рабочего тока начальной точки А
      i-step Шаг тока рабочих клеток А
      i-stop Конечная точка операционного тока ячейки А
       * Для получения дополнительной информации об этой модели посетите здесь
    • Найдите свои отчеты в папке Model_Name

    Экранная запись

    Экранная запись

Библиотека

  1. Статическая модель Amphlett 

    >>> from opem.Static.Amphlett import Static_Analysis
>>> Test_Vector = { " T " : 343.15 , " PH2 " : 1 , " PO2 " : 1 , " i-start " : 0 , " i-stop " : 75 , " i-step " : 0.1 , " A " : 50.6 , " l " : 0.0178 , " lambda " : 23 , " N " : 1 , " R " : 0 , " JMax " : 1.5 , " Name " : " Amphlett_Test " }
>>> data = Static_Analysis( InputMethod = Test_Vector, TestMode = True , PrintMode = False , ReportMode = False )
    Ключ Описание Тип
    Статус Статус моделирования Буль
    П Власть Список
    я Ячейка рабочего тока Список
    V. ФК напряжение Список
    Эф - Эффективность Список
    PH Тепловая мощность Список
    V0 Линейно-APX перехват Плавать
    K Линейный APX склон Плавать
    Eta_active ETA активация Список
    Eta_conc ETA концентрация Список
    Eta_omic Eta Ohmic Список
    Вежливый Расчетное напряжение FC Список
    • Для получения дополнительной информации об этой модели посетите здесь

  2. Larminie-Dicks Static Model 

    >>> from opem.Static.Larminie_Dicks import Static_Analysis
>>> Test_Vector = { " A " : 0.06 , " E0 " : 1.178 , " T " : 328.15 , " RM " : 0.0018 , " i_0 " : 0.00654 , " i_L " : 100.0 , " i_n " : 0.23 , " N " : 23 , " i-start " : 0.1 , " i-stop " : 98 , " i-step " : 0.1 , " Name " : " Larminiee_Test " }
>>> data = Static_Analysis( InputMethod = Test_Vector, TestMode = True , PrintMode = False , ReportMode = False )
    Ключ Описание Тип
    Статус Статус моделирования Буль
    П Власть Список
    я Ячейка рабочего тока Список
    V. ФК напряжение Список
    Эф - Эффективность Список
    PH Тепловая мощность Список
    V0 Линейно-APX перехват Плавать
    K Линейный APX склон Плавать
    Вежливый Расчетное напряжение FC Список
    • Для получения дополнительной информации об этой модели посетите здесь

  3. Статическая модель Camberline-Kim 

    >>> from opem.Static.Chamberline_Kim import Static_Analysis
>>> Test_Vector = { " A " : 50.0 , " E0 " : 0.982 , " b " : 0.0689 , " R " : 0.328 , " m " : 0.000125 , " n " : 9.45 , " N " : 1 , " i-start " : 1 , " i-stop " : 42.5 , " i-step " : 0.1 , " Name " : " Chamberline_Test " }
>>> data = Static_Analysis( InputMethod = Test_Vector, TestMode = True , PrintMode = False , ReportMode = False )
    Ключ Описание Тип
    Статус Статус моделирования Буль
    П Власть Список
    я Ячейка рабочего тока Список
    V. ФК напряжение Список
    Эф - Эффективность Список
    PH Тепловая мощность Список
    V0 Линейно-APX перехват Плавать
    K Линейный APX склон Плавать
    Вежливый Расчетное напряжение FC Список
    • Для получения дополнительной информации об этой модели посетите здесь

  4. Динамическая модель Padulles I 

    >>> from opem.Dynamic.Padulles1 import Dynamic_Analysis
>>> Test_Vector = { " T " : 343 , " E0 " : 0.6 , " N0 " : 88 , " KO2 " : 0.0000211 , " KH2 " : 0.0000422 , " tH2 " : 3.37 , " tO2 " : 6.74 , " B " : 0.04777 , " C " : 0.0136 , " Rint " : 0.00303 , " rho " : 1.168 , " qH2 " : 0.0004 , " i-start " : 0 , " i-stop " : 100 , " i-step " : 0.1 , " Name " : " PadullesI_Test " }
>>> data = Dynamic_Analysis( InputMethod = Test_Vector, TestMode = True , PrintMode = False , ReportMode = False )
    Ключ Описание Тип
    Статус Статус моделирования Буль
    П Власть Список
    я Ячейка рабочего тока Список
    V. ФК напряжение Список
    Эф - Эффективность Список
    PO2 Частичное давление Список
    PH2 Частичное давление Список
    PH Тепловая мощность Список
    V0 Линейно-APX перехват Плавать
    K Линейный APX склон Плавать
    Вежливый Расчетное напряжение FC Список
    • Для получения дополнительной информации об этой модели посетите здесь

  5. Динамическая модель Padulles Model II 

    >>> from opem.Dynamic.Padulles2 import Dynamic_Analysis
>>> Test_Vector = { " T " : 343 , " E0 " : 0.6 , " N0 " : 5 , " KO2 " : 0.0000211 , " KH2 " : 0.0000422 , " KH2O " : 0.000007716 , " tH2 " : 3.37 , " tO2 " : 6.74 , " tH2O " : 18.418 , " B " : 0.04777 , " C " : 0.0136 , " Rint " : 0.00303 , " rho " : 1.168 , " qH2 " : 0.0004 , " i-start " : 0.1 , " i-stop " : 100 , " i-step " : 0.1 , " Name " : " Padulles2_Test " }
>>> data = Dynamic_Analysis( InputMethod = Test_Vector, TestMode = True , PrintMode = False , ReportMode = False )
    Ключ Описание Тип
    Статус Статус моделирования Буль
    П Власть Список
    я Ячейка рабочего тока Список
    V. ФК напряжение Список
    Эф - Эффективность Список
    PO2 Частичное давление Список
    PH2 Частичное давление Список
    PH2O Частичное давление Список
    PH Тепловая мощность Список
    V0 Линейно-APX перехват Плавать
    K Линейный APX склон Плавать
    Вежливый Расчетное напряжение FC Список
    • Для получения дополнительной информации об этой модели посетите здесь

  6. Динамическая модель Padulles-Hauer 

    >>> from opem.Dynamic.Padulles_Hauer import Dynamic_Analysis
>>> Test_Vector = { " T " : 343 , " E0 " : 0.6 , " N0 " : 5 , " KO2 " : 0.0000211 , " KH2 " : 0.0000422 , " KH2O " : 0.000007716 , " tH2 " : 3.37 , " tO2 " : 6.74 , " t1 " : 2 , " t2 " : 2 , " tH2O " : 18.418 , " B " : 0.04777 , " C " : 0.0136 , " Rint " : 0.00303 , " rho " : 1.168 , " qMethanol " : 0.0002 , " CV " : 2 , " i-start " : 0.1 , " i-stop " : 100 , " i-step " : 0.1 , " Name " : " Padulles_Hauer_Test " }
>>> data = Dynamic_Analysis( InputMethod = Test_Vector, TestMode = True , PrintMode = False , ReportMode = False )
    Ключ Описание Тип
    Статус Статус моделирования Буль
    П Власть Список
    я Ячейка рабочего тока Список
    V. ФК напряжение Список
    Эф - Эффективность Список
    PO2 Частичное давление Список
    PH2 Частичное давление Список
    PH2O Частичное давление Список
    PH Тепловая мощность Список
    V0 Линейно-APX перехват Плавать
    K Линейный APX склон Плавать
    Вежливый Расчетное напряжение FC Список
    • Для получения дополнительной информации об этой модели посетите здесь

  7. Динамическая модель Padulles-Amphlett 

    >>> from opem.Dynamic.Padulles_Amphlett import Dynamic_Analysis
>>> Test_Vector = { " A " : 50.6 , " l " : 0.0178 , " lambda " : 23 , " JMax " : 1.5 , " T " : 343 , " N0 " : 5 , " KO2 " : 0.0000211 , " KH2 " : 0.0000422 , " KH2O " : 0.000007716 , " tH2 " : 3.37 , " tO2 " : 6.74 , " t1 " : 2 , " t2 " : 2 , " tH2O " : 18.418 , " rho " : 1.168 , " qMethanol " : 0.0002 , " CV " : 2 , " i-start " : 0.1 , " i-stop " : 75 , " i-step " : 0.1 , " Name " : " Padulles_Amphlett_Test " }
>>> data = Dynamic_Analysis( InputMethod = Test_Vector, TestMode = True , PrintMode = False , ReportMode = False )
    Ключ Описание Тип
    Статус Статус моделирования Буль
    П Власть Список
    я Ячейка рабочего тока Список
    V. ФК напряжение Список
    Эф - Эффективность Список
    PO2 Частичное давление Список
    PH2 Частичное давление Список
    PH2O Частичное давление Список
    PH Тепловая мощность Список
    V0 Линейно-APX перехват Плавать
    K Линейный APX склон Плавать
    Eta_active ETA активация Список
    Eta_conc ETA концентрация Список
    Eta_omic Eta Ohmic Список
    Вежливый Расчетное напряжение FC Список
    • Для получения дополнительной информации об этой модели посетите здесь

  8. Динамическая модель чакраборти 

    >>> from opem.Dynamic.Chakraborty import Dynamic_Analysis
>>> Test_Vector = { " T " : 1273 , " E0 " : 0.6 , " u " : 0.8 , " N0 " : 1 , " R " : 3.28125 * 10 ** ( - 3 ), " KH2O " : 0.000281 , " KH2 " : 0.000843 , " KO2 " : 0.00252 , " rho " : 1.145 , " i-start " : 0.1 , " i-stop " : 300 , " i-step " : 0.1 , " Name " : " Chakraborty_Test " }
>>> data = Dynamic_Analysis( InputMethod = Test_Vector, TestMode = True , PrintMode = False , ReportMode = False )
    Ключ Описание Тип
    Статус Статус моделирования Буль
    П Власть Список
    я Ячейка рабочего тока Список
    V. ФК напряжение Список
    Эф - Эффективность Список
    PO2 Частичное давление Список
    PH2 Частичное давление Список
    PH2O Частичное давление Список
    PH Тепловая мощность Список
    Добность Нернста Добность Нернста Список
    Омическая потеря Омическая потеря Список
    V0 Линейно-APX перехват Плавать
    K Линейный APX склон Плавать
    Вежливый Расчетное напряжение FC Список
    • Для получения дополнительной информации об этой модели посетите здесь

    Параметры

    1. TestMode : активный режим тестирования и получить/вернуть данные как dict , (по умолчанию: False )
    2. ReportMode .html генерируйте True .opem .csv
    3. PrintMode : Печать управления в консоли, (по умолчанию: True )
    4. Folder : папка отчетов, (по умолчанию: os.getcwd() )

    Примечание

    • Возвращение типа: dict

Телеграмма бот

  • Отправить /start команды для опема бота
  • Выберите модели из меню
  • Отправьте свой тестовый вектор в соответствии с шаблоном
  • Загрузите свои результаты

Попробуйте Opem в своем браузере!

OPEM можно использовать онлайн в интерактивных ноутбуках Jupyter через сервис Binder! Попробуйте сейчас! :

  • Проверьте .ipynb файлы в папке Documents
  • Редактировать и выполнить каждую часть примечаний, шаг за шагом с кнопки «Верхняя панель».
  • Для выполнения полного моделирования вы можете редактировать Test_Vector в разделе Full Run

Проблемы и отчеты об ошибках

Просто заполните проблему и опишите ее. Мы проверим это как можно скорее! Или отправьте электронное письмо по адресу [email protected].

Вы также можете присоединиться к нашему серверу Discord

Выходы

  1. HTML
  2. CSV
  3. Опем

Спасибо

  • Chart.js
  • Pyinstaller
  • Draw.io
  • Zahra Mobasher (дизайн логотипа)

Ссылка

1- JC Amphlett, RM Baumert, RF Mann, Ba Peppley и PR Roberge. 1995. «Производительное моделирование твердого полимерного электролитного топливного элемента Ballard Mark IV». J. Electrochem. Соц (Electrochemical Society, Inc.) 142 (1): 9-15. doi: 10.1149/1.2043959.
2- Джеферсон М. Корреа, Феликс А. Фаррет, Владимир А. Попов, Марсело Г. Симос. 2005. «Анализ чувствительности параметров моделирования, используемых при моделировании протонных обменных топливных элементов». IEEE транзакции на преобразование энергии (IEEE) 20 (1): 211-218. doi: 10.1109/tec.2004.842382.
3- Джунбом Ким, Сон-Мин Ли, Супраманиам Шринивасан, Чарльз Э. Чемберлин. 1995. «Моделирование производительности топливных элементов топливных элементов протона обмена с эмпирическим уравнением». Журнал электрохимического общества (Электрохимическое общество) 142 (8): 2670-2674. doi: 10.1149/1.2050072.
4- I. Sadli, P. Thounthong, J.-P. Мартин, С. Раэль, Б. Дават. 2006. «Поведение PEMFC, поставляющего статический конвертер низкого напряжения». Журнал источников питания (Elsevier) 156: 119–125. doi: 10.1016/j.jpowsour.2005.08.021.
5- J. Padulles, GW Ault, JR McDonald. 2000. «Интегрированная динамическая модель завода SOFC для моделирования энергосистемы». Журнал источников питания (Elsevier) 86 (1-2): 495-500. doi: 10.1016/s0378-7753 (99) 00430-9.
6- Hauer, K.-H. 2001. «Инструмент анализа для оборудования и программного обеспечения для автомобилей топливных элементов (управления) с применением для сравнения экономии топлива для дизайнов альтернативных систем». Доктор философии Диссертация, транспортные технологии и политика, Калифорнийский университет Дэвис.
7- A. Saadi, M. Becherif, A. Aboubou, My Ayad. 2013. «Сравнение статических моделей топливных элементов протоновых мембраны». Возобновляемая энергия (Elsevier) 56: 64-71. doi: dx.doi.org/10.1016/j.renene.2012.10.012.
8- Диего Ферольди, Марта Басуалдо. 2012. "Описание системы топливных элементов PEM". Зеленая энергия и технология (Springer) 49-72. doi: 10.1007/978-1-84996-184-4_2
9- Готтесфельд, Шимшон. ND Полимерный топливный элемент электролита: проблемы с материалами в источнике питания, заправленном водородом. http://physics.oregonstate.edu/~hetheriw/energy/topics/doc/electrochemistry/fc/basic/the_polymer_electrolyte_fuel_cell.htm
10- Мохамед Бегериф, Айча Саади, Даниэль Хиссель, Абденсер Абубу, Мохамед Ячин Аяд. 2011. «Статические и динамические модели топливных элементов протонов -обмена мембраны». Журнал углеводородов шахт и экологических исследований 2 (1)
11- Larminie, J., Dicks, A. & McDonald, MS 2003. Объясненные системы топливных элементов (Vol. 2, pp. 207-225). Чичестер, Великобритания: Дж. Уайли. doi: 10.1002/9781118706992.
12- Rho, YW, Srinivasan, S. & Kho, YT 1994. Теоретический анализ. '' Журнал электрохимического общества, 141 (8), 2089-2096. doi: 10.1149/1.2055066.
13- U. Chakraborty, новая модель для постоянного использования топлива и постоянного потока топлива в топливных элементах, Appl. Наука 9 (2019) 1066. https://doi.org/10.3390/app9061066.

Цитировать

Если вы используете Opem в своем исследовании, пожалуйста, укажите эту статью:

 @Article {haghighi2018,
  doi = {10.21105/joss.00676},
  url = {https://doi.org/10.21105/joss.00676},
  Год = {2018},
  месяц = ​​{jul},
  Publisher = {Open Journal},
  том = {3},
  number = {27},
  pages = {676},
  Автор = {Сепанд Хагиги и Касра Аскари и Сармин Хамиди и Мохаммад Махди Рахими},
  title = {{opem}: Open Source {PEM} Моделирование ячейки},
  Journal = {Журнал программного обеспечения с открытым исходным кодом}
}

Скачать opem.bib (формат Bibtex)

Джосс
Зенодо

Покажите свою поддержку

Светь это репо

Дайте ️, если этот проект помог вам!

Пожертвовать нашему проекту

Если вам нравится наш проект, и мы надеемся, что вы это сделаете, не могли бы вы поддержать нас? Наш проект не и никогда не будет работать на прибыль. Нам нужны деньги, чтобы мы могли продолжать делать то, что мы делаем ;-).

Расширять
Дополнительная информация
Связанные приложения
Рекомендуем вам
Связанные новости Все