首页>JSP源码>其他类别
下载

目录

  • 什么是PEM？
  • 概述
  • 安装
  • 用法
    • 可执行
    • 图书馆
    • 电报机器人
    • 在浏览器中尝试使用OPEM！
    • MATLAB
  • 问题和错误报告
  • 贡献
  • 输出
  • 谢谢
  • 参考
  • 引用
  • 作者
  • 执照
  • 表示您的支持
  • ChangElog
  • 行为守则

概述

质子交换膜燃料电池（PEMFC）的建模和仿真可以作为可再生能源研究与开发的强大工具。开源PEMFC仿真工具（OPEM）是评估质子交换膜燃料电池性能的建模工具。该软件包是预测PEMFC最佳操作参数的模型（静态/动态）的组合。 OPEM包含将作为输入的通用模型，不仅是操作变量的值，例如阳极和阴极馈电气体，压力和组成，细胞温度和电流密度，还包括细胞参数，包括活动面积和膜厚度。此外，在OPEM中提出的一些不同的PEMFC模型，只专注于一个特定的FC堆栈，而另一些PEMFC则考虑了一部分或所有辅助机构，例如改革者。 OPEM是PEMFC模型协作开发的平台。

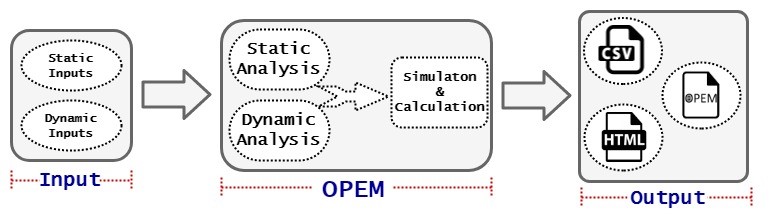
图1。 OPEM框图

开放式枢纽
PYPI计数器
Github星星
分支掌握发展
CI
代码质量

用法

可执行

  • 打开CMD （Windows）或Terminal （UNIX）

  • 运行opem或python -m opem （或运行OPEM.exe ）

  • 输入PEM单元参数（或运行标准测试向量）

    1. Amphlett静态模型

      输入描述单元
      t细胞操作温度k
      PH2部分压力ATM
      PO2部分压力ATM
      我开始细胞操作当前起点一个
      我步单元操作电流步骤一个
      我停留电池操作电流终点一个
      一个活动区域CM^2
      l膜厚度厘米
      Lambda可调参数，最小值为14，最大值为23 - -
      R（*可选） R电子欧姆
      jmax最大电流密度A/（CM^2）
      n单细胞的数量 - -
      *有关此模型的更多信息，请访问此处

    2. Larminie-Dicks静态模型

      输入描述单元
      E0燃料电池可逆无损耗电压v
      一个塔菲尔线的斜率v
      t细胞操作温度k
      我开始细胞操作当前起点一个
      我步单元操作电流步骤一个
      我停留电池操作电流终点一个
      在内部电流一个
      I_0过电压开始从零移动的交换电流一个
      I_L限制电流一个
      RM膜和接触电阻欧姆
      n单细胞的数量 - -
      *有关此模型的更多信息，请访问此处

    3. Charbleline-Kim静态模型

      输入描述单元
      E0开路电压v
      b塔菲尔还原的参数v
      r反抗ohm.cm^2
      我开始细胞操作当前起点一个
      我步单元操作电流步骤一个
      我停留电池操作电流终点一个
      一个活动区域CM^2
      m扩散的参数v
      n扩散的参数（a^-1）（cm^2）
      n单细胞的数量 - -
      *有关此模型的更多信息，请访问此处

    4. 帕杜斯动态模型I

      输入描述单元
      E0没有负载电压v
      t燃料电池温度k
      KH2氢阀常数kmol.s^（-1）.ATM^（-1）
      KO2氧气阀常数kmol.s^（-1）.ATM^（-1）
      Th2氢时间常数s
      TO2氧时间常数s
      b激活电压常数v
      c激活常数参数a^（-1）
      rint燃料电池内部电阻欧姆
      罗氢 - 氧气流量比 - -
      QH2氢气流kmol/s
      N0细胞数量 - -
      我开始细胞操作当前起点一个
      我步单元操作电流步骤一个
      我停留电池操作电流终点一个
      *有关此模型的更多信息，请访问此处

    5. Paduls Dynamic Model II

      输入描述单元
      E0没有负载电压v
      t燃料电池温度k
      KH2氢阀常数kmol.s^（-1）.ATM^（-1）
      KH2O水阀常数kmol.s^（-1）.ATM^（-1）
      KO2氧气阀常数kmol.s^（-1）.ATM^（-1）
      Th2氢时间常数s
      th2o水位时间常数s
      TO2氧时间常数s
      b激活电压常数v
      c激活常数参数a^（-1）
      rint燃料电池内部电阻欧姆
      罗氢 - 氧气流量比 - -
      QH2氢气流kmol/s
      N0细胞数量 - -
      我开始细胞操作当前起点一个
      我步单元操作电流步骤一个
      我停留电池操作电流终点一个
      *有关此模型的更多信息，请访问此处

    6. Paduls-Hauer动态模型

      输入描述单元
      E0没有负载电压v
      t燃料电池温度k
      KH2氢阀常数kmol.s^（-1）.ATM^（-1）
      KH2O水阀常数kmol.s^（-1）.ATM^（-1）
      KO2氧气阀常数kmol.s^（-1）.ATM^（-1）
      Th2氢时间常数s
      th2o水位时间常数s
      TO2氧时间常数s
      T1改革器时间不变s
      T2改革器时间不变s
      b激活电压常数v
      c激活常数参数a^（-1）
      简历转换因子 - -
      rint燃料电池内部电阻欧姆
      罗氢 - 氧气流量比 - -
      Qmethanol甲醇的摩尔流动kmol/s
      N0细胞数量 - -
      我开始细胞操作当前起点一个
      我步单元操作电流步骤一个
      我停留电池操作电流终点一个
      *有关此模型的更多信息，请访问此处

    7. PADULLES-AMPHLETT动态模型

      输入描述单元
      E0没有负载电压v
      t燃料电池温度k
      KH2氢阀常数kmol.s^（-1）.ATM^（-1）
      KH2O水阀常数kmol.s^（-1）.ATM^（-1）
      KO2氧气阀常数kmol.s^（-1）.ATM^（-1）
      Th2氢时间常数s
      th2o水位时间常数s
      TO2氧时间常数s
      T1改革器时间不变s
      T2改革器时间不变s
      一个活动区域CM^2
      l膜厚度厘米
      Lambda可调参数，最小值为14，最大值为23 - -
      R（*可选） R电子欧姆
      jmax最大电流密度A/（CM^2）
      简历转换因子 - -
      罗氢 - 氧气流量比 - -
      Qmethanol甲醇的摩尔流动kmol/s
      N0细胞数量 - -
      我开始细胞操作当前起点一个
      我步单元操作电流步骤一个
      我停留电池操作电流终点一个
      *有关此模型的更多信息，请访问此处

    8. Chakraborty动态模型

      输入描述单元
      E0没有负载电压v
      t细胞操作温度k
      KH2氢阀常数kmol.s^（-1）.ATM^（-1）
      KH2O水阀常数kmol.s^（-1）.ATM^（-1）
      KO2氧气阀常数kmol.s^（-1）.ATM^（-1）
      罗氢 - 氧气流量比 - -
      rint燃料电池内部电阻欧姆
      N0细胞数量 - -
      你燃料利用率 - -
      我开始细胞操作当前起点一个
      我步单元操作电流步骤一个
      我停留电池操作电流终点一个
      *有关此模型的更多信息，请访问此处
    • 在Model_Name文件夹中查找您的报告

    屏幕记录

    屏幕记录

图书馆

  1. Amphlett静态模型

    >>> from opem.Static.Amphlett import Static_Analysis
>>> Test_Vector = { " T " : 343.15 , " PH2 " : 1 , " PO2 " : 1 , " i-start " : 0 , " i-stop " : 75 , " i-step " : 0.1 , " A " : 50.6 , " l " : 0.0178 , " lambda " : 23 , " N " : 1 , " R " : 0 , " JMax " : 1.5 , " Name " : " Amphlett_Test " }
>>> data = Static_Analysis( InputMethod = Test_Vector, TestMode = True , PrintMode = False , ReportMode = False )
    钥匙描述类型
    地位模拟状态布尔
    p力量列表
    我电池操作电流列表
    v FC电压列表
    eff效率列表
    ph热力列表
    v0线性APX截距漂浮
    k线性apx斜率漂浮
    eta_active ETA激活列表
    eta_conc ETA浓度列表
    eta_ohmic Eta Ohmic列表
    VE估计的FC电压列表
    • 有关此模型的更多信息，请访问此处

  2. Larminie-Dicks静态模型

    >>> from opem.Static.Larminie_Dicks import Static_Analysis
>>> Test_Vector = { " A " : 0.06 , " E0 " : 1.178 , " T " : 328.15 , " RM " : 0.0018 , " i_0 " : 0.00654 , " i_L " : 100.0 , " i_n " : 0.23 , " N " : 23 , " i-start " : 0.1 , " i-stop " : 98 , " i-step " : 0.1 , " Name " : " Larminiee_Test " }
>>> data = Static_Analysis( InputMethod = Test_Vector, TestMode = True , PrintMode = False , ReportMode = False )
    钥匙描述类型
    地位模拟状态布尔
    p力量列表
    我电池操作电流列表
    v FC电压列表
    eff效率列表
    ph热力列表
    v0线性APX截距漂浮
    k线性apx斜率漂浮
    VE估计的FC电压列表
    • 有关此模型的更多信息，请访问此处

  3. Charbleline-Kim静态模型

    >>> from opem.Static.Chamberline_Kim import Static_Analysis
>>> Test_Vector = { " A " : 50.0 , " E0 " : 0.982 , " b " : 0.0689 , " R " : 0.328 , " m " : 0.000125 , " n " : 9.45 , " N " : 1 , " i-start " : 1 , " i-stop " : 42.5 , " i-step " : 0.1 , " Name " : " Chamberline_Test " }
>>> data = Static_Analysis( InputMethod = Test_Vector, TestMode = True , PrintMode = False , ReportMode = False )
    钥匙描述类型
    地位模拟状态布尔
    p力量列表
    我电池操作电流列表
    v FC电压列表
    eff效率列表
    ph热力列表
    v0线性APX截距漂浮
    k线性apx斜率漂浮
    VE估计的FC电压列表
    • 有关此模型的更多信息，请访问此处

  4. 帕杜斯动态模型I 

    >>> from opem.Dynamic.Padulles1 import Dynamic_Analysis
>>> Test_Vector = { " T " : 343 , " E0 " : 0.6 , " N0 " : 88 , " KO2 " : 0.0000211 , " KH2 " : 0.0000422 , " tH2 " : 3.37 , " tO2 " : 6.74 , " B " : 0.04777 , " C " : 0.0136 , " Rint " : 0.00303 , " rho " : 1.168 , " qH2 " : 0.0004 , " i-start " : 0 , " i-stop " : 100 , " i-step " : 0.1 , " Name " : " PadullesI_Test " }
>>> data = Dynamic_Analysis( InputMethod = Test_Vector, TestMode = True , PrintMode = False , ReportMode = False )
    钥匙描述类型
    地位模拟状态布尔
    p力量列表
    我电池操作电流列表
    v FC电压列表
    eff效率列表
    PO2部分压力列表
    PH2部分压力列表
    ph热力列表
    v0线性APX截距漂浮
    k线性apx斜率漂浮
    VE估计的FC电压列表
    • 有关此模型的更多信息，请访问此处

  5. Paduls Dynamic Model II 

    >>> from opem.Dynamic.Padulles2 import Dynamic_Analysis
>>> Test_Vector = { " T " : 343 , " E0 " : 0.6 , " N0 " : 5 , " KO2 " : 0.0000211 , " KH2 " : 0.0000422 , " KH2O " : 0.000007716 , " tH2 " : 3.37 , " tO2 " : 6.74 , " tH2O " : 18.418 , " B " : 0.04777 , " C " : 0.0136 , " Rint " : 0.00303 , " rho " : 1.168 , " qH2 " : 0.0004 , " i-start " : 0.1 , " i-stop " : 100 , " i-step " : 0.1 , " Name " : " Padulles2_Test " }
>>> data = Dynamic_Analysis( InputMethod = Test_Vector, TestMode = True , PrintMode = False , ReportMode = False )
    钥匙描述类型
    地位模拟状态布尔
    p力量列表
    我电池操作电流列表
    v FC电压列表
    eff效率列表
    PO2部分压力列表
    PH2部分压力列表
    PH2O部分压力列表
    ph热力列表
    v0线性APX截距漂浮
    k线性apx斜率漂浮
    VE估计的FC电压列表
    • 有关此模型的更多信息，请访问此处

  6. Paduls-Hauer动态模型

    >>> from opem.Dynamic.Padulles_Hauer import Dynamic_Analysis
>>> Test_Vector = { " T " : 343 , " E0 " : 0.6 , " N0 " : 5 , " KO2 " : 0.0000211 , " KH2 " : 0.0000422 , " KH2O " : 0.000007716 , " tH2 " : 3.37 , " tO2 " : 6.74 , " t1 " : 2 , " t2 " : 2 , " tH2O " : 18.418 , " B " : 0.04777 , " C " : 0.0136 , " Rint " : 0.00303 , " rho " : 1.168 , " qMethanol " : 0.0002 , " CV " : 2 , " i-start " : 0.1 , " i-stop " : 100 , " i-step " : 0.1 , " Name " : " Padulles_Hauer_Test " }
>>> data = Dynamic_Analysis( InputMethod = Test_Vector, TestMode = True , PrintMode = False , ReportMode = False )
    钥匙描述类型
    地位模拟状态布尔
    p力量列表
    我电池操作电流列表
    v FC电压列表
    eff效率列表
    PO2部分压力列表
    PH2部分压力列表
    PH2O部分压力列表
    ph热力列表
    v0线性APX截距漂浮
    k线性apx斜率漂浮
    VE估计的FC电压列表
    • 有关此模型的更多信息，请访问此处

  7. PADULLES-AMPHLETT动态模型

    >>> from opem.Dynamic.Padulles_Amphlett import Dynamic_Analysis
>>> Test_Vector = { " A " : 50.6 , " l " : 0.0178 , " lambda " : 23 , " JMax " : 1.5 , " T " : 343 , " N0 " : 5 , " KO2 " : 0.0000211 , " KH2 " : 0.0000422 , " KH2O " : 0.000007716 , " tH2 " : 3.37 , " tO2 " : 6.74 , " t1 " : 2 , " t2 " : 2 , " tH2O " : 18.418 , " rho " : 1.168 , " qMethanol " : 0.0002 , " CV " : 2 , " i-start " : 0.1 , " i-stop " : 75 , " i-step " : 0.1 , " Name " : " Padulles_Amphlett_Test " }
>>> data = Dynamic_Analysis( InputMethod = Test_Vector, TestMode = True , PrintMode = False , ReportMode = False )
    钥匙描述类型
    地位模拟状态布尔
    p力量列表
    我电池操作电流列表
    v FC电压列表
    eff效率列表
    PO2部分压力列表
    PH2部分压力列表
    PH2O部分压力列表
    ph热力列表
    v0线性APX截距漂浮
    k线性apx斜率漂浮
    eta_active ETA激活列表
    eta_conc ETA浓度列表
    eta_ohmic Eta Ohmic列表
    VE估计的FC电压列表
    • 有关此模型的更多信息，请访问此处

  8. Chakraborty动态模型

    >>> from opem.Dynamic.Chakraborty import Dynamic_Analysis
>>> Test_Vector = { " T " : 1273 , " E0 " : 0.6 , " u " : 0.8 , " N0 " : 1 , " R " : 3.28125 * 10 ** ( - 3 ), " KH2O " : 0.000281 , " KH2 " : 0.000843 , " KO2 " : 0.00252 , " rho " : 1.145 , " i-start " : 0.1 , " i-stop " : 300 , " i-step " : 0.1 , " Name " : " Chakraborty_Test " }
>>> data = Dynamic_Analysis( InputMethod = Test_Vector, TestMode = True , PrintMode = False , ReportMode = False )
    钥匙描述类型
    地位模拟状态布尔
    p力量列表
    我电池操作电流列表
    v FC电压列表
    eff效率列表
    PO2部分压力列表
    PH2部分压力列表
    PH2O部分压力列表
    ph热力列表
    内特的收益内特的收益列表
    欧姆损失欧姆损失列表
    v0线性APX截距漂浮
    k线性apx斜率漂浮
    VE估计的FC电压列表
    • 有关此模型的更多信息，请访问此处

    参数

    1. TestMode ：活动测试模式并获取/返回数据如dict （默认： False ）
    2. ReportMode ：生成报告（ .csv ， .opem ， .html ）并打印在控制台中（默认： True ）
    3. PrintMode ：控制台中的控制打印，（默认： True ）
    4. Folder ：报告文件夹，（默认： os.getcwd() ）

    笔记

    • 返回类型： dict

电报机器人

  • 发送/start命令到opem bot
  • 从菜单中选择型号
  • 根据模板发送测试向量
  • 下载您的结果

在浏览器中尝试使用OPEM！

OPEM可以通过粘合剂服务在交互式jupyter笔记本中在线使用！现在尝试一下！ ：

  • 在Documents夹中检查.ipynb文件
  • 编辑并执行注释的每个部分，逐步从顶部面板按Run按钮
  • 对于执行完整的模拟，您可以在Full Run部分中编辑Test_Vector

问题和错误报告

只需填写一个问题并描述它。我们将尽快检查一下！或发送电子邮件至[email protected]。

您也可以加入我们的Discord服务器

输出

  1. html
  2. CSV
  3. OPEM

谢谢

  • 图表
  • Pyinstaller
  • draw.io
  • Zahra Mobasher（徽标设计）

参考

1- JC Amphlett，RM Baumert，RF Mann，Ba Peppley和Pr Roberge。 1995年。“巴拉德标记IV固体聚合物电解质燃料电池的性能建模”。 J. Electrochem。 Soc。 （电化学协会，公司）142（1）：9-15。 doi：10.1149/1.2043959。
2- Jeferson M. Correa，Felix A. Farret，Vladimir A. Popov，Marcelo G. Simoes。 2005。“对模拟质子交换膜燃料电池的建模参数的灵敏度分析。” IEEE能源转换（IEEE）20（1）：211-218的IEEE交易。 doi：10.1109/tec.2004.842382。
3- Junbom Kim，Seong Lee，Supramaniam Srinivasan，Charles E. Chamberlin。 1995年。“具有经验方程的质子交换膜燃料电池性能的建模”。电化学学会杂志（电化学学会）142（8）：2670-2674。 doi：10.1149/1.2050072。
4- I. Sadli，P。Thounthong，J.-P。马丁，S。Rael，B。Davat。 2006。“ PEMFC提供低压静态转换器的行为”。电源杂志（Elsevier）156：119–125。 doi：10.1016/j.jpowsour.2005.08.021。
5- J. Paduls，GW Ault，Jr McDonald。 2000。“用于电源系统模拟的集成SOFC植物动力学模型”。电源杂志（Elsevier）86（1-2）：495-500。 doi：10.1016/s0378-7753（99）00430-9。
6-豪尔，K.-H。 2001年。“用于燃料电池汽车硬件和软件（控件）的分析工具，并应用了替代系统设计的燃料经济性比较。”博士加利福尼亚大学戴维斯分校的论文，交通技术与政策。
7- A. Saadi，M。Bechherif，A。Aboubou，我的Ayad。 2013。“质子交换膜燃料电池静态模型的比较”。可再生能源（Elsevier）56：64-71。 doi：dx.doi.org/10.1016/j.renene.2012.10.012。
8-Diego Feroldi，Marta Basualdo。 2012。“ PEM燃料电池系统的描述”。绿色能源与技术（Springer）49-72。 doi：10.1007/978-1-84996-184-4_2
9- Gottesfeld，Shimshon。 ND聚合物电解质燃料电池：氢燃料电源中的材料问题。 http://physics.oregonstate.edu/~hetheriw/ energy/topics/doc/doc/electrochemistry/fc/basic/the_polymer_electrolyte_fuel_cell.htm
10-穆罕默德·贝克里夫（Mohamed Becherif），艾萨·萨迪（AïchaSaadi），丹尼尔·赫斯塞尔（Daniel Hissel），阿巴纳克·阿布布（Abdennacer Aboubou），穆罕默德·亚辛·艾亚德（Mohamed Yacine Ayad）。 2011。“静态和动态质子交换膜燃料电池模型”。烃矿与环境研究杂志2（1）
11- Larminie，J.，Dicks，A。，＆McDonald，MS 2003。解释的燃料电池系统（第2卷，第207-225页）。英国奇切斯特：J。Wiley。 doi：10.1002/9781118706992。
12- Rho，YW，Srinivasan，S。，＆Kho，YT 1994。''使用O 2/HE，O 2/AR和O 2/N 2混合物II的质子交换膜燃料电池中的质量传输现象。理论分析。''电化学学会杂志，141（8），2089-2096。 doi：10.1149/1.2055066。
13- U. Chakraborty，一种新的模型，用于恒定燃料利用和燃料电池中恒定的燃料流量。科学。 9（2019）1066。https：//doi.org/10.3390/App9061066。

引用

如果您在研究中使用OPEM，请引用本文：

 @Article {Haghighi2018，
  doi = {10.21105/joss.00676}，
  url = {https://doi.org/10.21105/joss.00676}，
  年= {2018}，
  月= {jul}，
  Publisher = {the Open Journal}，
  音量= {3}，
  数字= {27}，
  页= {676}，
  作者= {Sepand Haghighi和Kasra Askari和Sarmin Hamidi和Mohammad Mahdi Rahimi}，
  title = {{opem}：开源{pem}单元模拟工具}，
  日记= {开源软件期刊}
}

下载opem.bib（bibtex格式）

乔斯
Zenodo

表示您的支持

明星这个仓库

如果这个项目对您有所帮助，请给！

向我们的项目捐款

如果您喜欢我们的项目，我们希望您能做到，请您支持我们吗？我们的项目不是，也永远不会为盈利而努力。我们需要这笔钱，以便我们可以继续做自己的工作;-)。

展开
附加信息
相关应用
为您推荐
相关资讯 全部