
A modelagem e a simulação de células de combustível de membrana de troca de prótons (PEMFC) podem funcionar como uma ferramenta poderosa na pesquisa e desenvolvimento de fontes de energia renovável. A ferramenta de simulação PEMFC de código aberto (OPEM) é uma ferramenta de modelagem para avaliar o desempenho das células de combustível de membrana de troca de prótons. Este pacote é uma combinação de modelos (estáticos/dinâmicos) que prevê os parâmetros operacionais ótimos do PEMFC. O OPEM continha modelos genéricos que aceitarão como entrada, não apenas os valores das variáveis operacionais, como ânodo e cátodo, gases de alimentação, pressão e composições, temperatura celular e densidade de corrente, mas também parâmetros celulares, incluindo a área ativa e a espessura da membrana. Além disso, alguns dos diferentes modelos de PEMFC que foram propostos no Opem, apenas se concentram em uma pilha FC em particular, e outros levam em consideração uma parte ou todos os auxiliares, como reformadores. O OPEM é uma plataforma para o desenvolvimento colaborativo de modelos PEMFC.
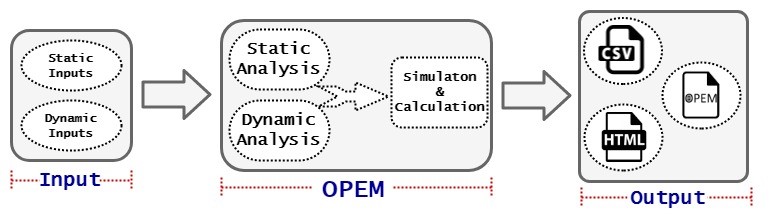
Fig1. Diagrama de blocos de opem
| Hub aberto | |
| Contador de Pypi | |
| Estrelas do Github |
| Filial | mestre | desenvolver |
| CI |  |  |
| Qualidade de código |
Abra CMD (Windows) ou Terminal (UNIX)
Execute opem ou python -m opem (ou execute OPEM.exe )
Digite parâmetros de células PEM (ou execute vetores de teste padrão)
Modelo estático Amphlett
| Entrada | Descrição | Unidade |
| T | Temperatura de operação da célula | K |
| Ph2 | Pressão parcial | atm |
| PO2 | Pressão parcial | atm |
| I-Start | Cell Operating Current Start Point | UM |
| I-step | Etapa atual de operação de células | UM |
| Eu-Stop | Cell Operating Current End Point | UM |
| UM | Área ativa | cm^2 |
| l | Espessura da membrana | cm |
| Lambda | Um parâmetro ajustável com um valor mínimo de 14 e valor máximo de 23 | - |
| R (*opcional) | R-Eletrônico | ohm |
| Jmax | Densidade de corrente máxima | A/(cm^2) |
| N | Número de células únicas | - |
Modelo estático Larminie-Dicks
| Entrada | Descrição | Unidade |
| E0 | Célula de combustível reversível sem tensão de perda | V |
| UM | A inclinação da linha de Tafel | V |
| T | Temperatura de operação da célula | K |
| I-Start | Cell Operating Current Start Point | UM |
| I-step | Etapa atual de operação de células | UM |
| Eu-Stop | Cell Operating Current End Point | UM |
| em | Corrente interna | UM |
| i_0 | Troca de corrente na qual a sobretensão começa a se mover de zero | UM |
| i_l | Limitando a corrente | UM |
| Rm | A membrana e as resistências de contato | ohm |
| N | Número de células únicas | - |
Modelo estático da Chamberline-Kim
| Entrada | Descrição | Unidade |
| E0 | Tensão de circuito aberto | V |
| b | Parâmetro de Tafel para a redução de oxigênio | V |
| R | Resistência | Ohm.cm^2 |
| I-Start | Cell Operating Current Start Point | UM |
| I-step | Etapa atual de operação de células | UM |
| Eu-Stop | Cell Operating Current End Point | UM |
| UM | Área ativa | cm^2 |
| m | Parâmetros da difusão | V |
| n | Parâmetros da difusão | (A^-1) (cm^2) |
| N | Número de células únicas | - |
Padulles Modelo Dinâmico I
| Entrada | Descrição | Unidade |
| E0 | Sem tensão de carga | V |
| T | Temperatura da célula de combustível | K |
| KH2 | Válvula de hidrogênio constante | Kmol.s^(-1) .ATM^(-1) |
| KO2 | Válvula de oxigênio constante | Kmol.s^(-1) .ATM^(-1) |
| Th2 | Tempo de hidrogênio constante | s |
| to2 | Tempo de oxigênio constante | s |
| B | Constante de tensão de ativação | V |
| C | Parâmetro constante de ativação | A^(-1) |
| Rint | Resistência interna da célula de combustível | ohm |
| Rho | Razão de fluxo de hidrogênio-oxigênio | - |
| QH2 | Fluxo molar de hidrogênio | kmol/s |
| N0 | Número de células | - |
| I-Start | Cell Operating Current Start Point | UM |
| I-step | Etapa atual de operação de células | UM |
| Eu-Stop | Cell Operating Current End Point | UM |
Padulles Dynamic Modelo II
| Entrada | Descrição | Unidade |
| E0 | Sem tensão de carga | V |
| T | Temperatura da célula de combustível | K |
| KH2 | Válvula de hidrogênio constante | Kmol.s^(-1) .ATM^(-1) |
| KH2O | Válvula de água constante | Kmol.s^(-1) .ATM^(-1) |
| KO2 | Válvula de oxigênio constante | Kmol.s^(-1) .ATM^(-1) |
| Th2 | Tempo de hidrogênio constante | s |
| Th2o | Tempo de água constante | s |
| to2 | Tempo de oxigênio constante | s |
| B | Constante de tensão de ativação | V |
| C | Parâmetro constante de ativação | A^(-1) |
| Rint | Resistência interna da célula de combustível | ohm |
| Rho | Razão de fluxo de hidrogênio-oxigênio | - |
| QH2 | Fluxo molar de hidrogênio | kmol/s |
| N0 | Número de células | - |
| I-Start | Cell Operating Current Start Point | UM |
| I-step | Etapa atual de operação de células | UM |
| Eu-Stop | Cell Operating Current End Point | UM |
Modelo dinâmico de Padulles-Hauer
| Entrada | Descrição | Unidade |
| E0 | Sem tensão de carga | V |
| T | Temperatura da célula de combustível | K |
| KH2 | Válvula de hidrogênio constante | Kmol.s^(-1) .ATM^(-1) |
| KH2O | Válvula de água constante | Kmol.s^(-1) .ATM^(-1) |
| KO2 | Válvula de oxigênio constante | Kmol.s^(-1) .ATM^(-1) |
| Th2 | Tempo de hidrogênio constante | s |
| Th2o | Tempo de água constante | s |
| to2 | Tempo de oxigênio constante | s |
| T1 | Tempo de reformador constante | s |
| T2 | Tempo de reformador constante | s |
| B | Constante de tensão de ativação | V |
| C | Parâmetro constante de ativação | A^(-1) |
| cv | Fator de conversão | - |
| Rint | Resistência interna da célula de combustível | ohm |
| Rho | Razão de fluxo de hidrogênio-oxigênio | - |
| Qmethanol | Fluxo molar de metanol | kmol/s |
| N0 | Número de células | - |
| I-Start | Cell Operating Current Start Point | UM |
| I-step | Etapa atual de operação de células | UM |
| Eu-Stop | Cell Operating Current End Point | UM |
Modelo dinâmico de Padulles-Aprhlett
| Entrada | Descrição | Unidade |
| E0 | Sem tensão de carga | V |
| T | Temperatura da célula de combustível | K |
| KH2 | Válvula de hidrogênio constante | Kmol.s^(-1) .ATM^(-1) |
| KH2O | Válvula de água constante | Kmol.s^(-1) .ATM^(-1) |
| KO2 | Válvula de oxigênio constante | Kmol.s^(-1) .ATM^(-1) |
| Th2 | Tempo de hidrogênio constante | s |
| Th2o | Tempo de água constante | s |
| to2 | Tempo de oxigênio constante | s |
| T1 | Tempo de reformador constante | s |
| T2 | Tempo de reformador constante | s |
| UM | Área ativa | cm^2 |
| l | Espessura da membrana | cm |
| Lambda | Um parâmetro ajustável com um valor mínimo de 14 e valor máximo de 23 | - |
| R (*opcional) | R-Eletrônico | ohm |
| Jmax | Densidade de corrente máxima | A/(cm^2) |
| cv | Fator de conversão | - |
| Rho | Razão de fluxo de hidrogênio-oxigênio | - |
| Qmethanol | Fluxo molar de metanol | kmol/s |
| N0 | Número de células | - |
| I-Start | Cell Operating Current Start Point | UM |
| I-step | Etapa atual de operação de células | UM |
| Eu-Stop | Cell Operating Current End Point | UM |
Modelo dinâmico de Chakraborty
| Entrada | Descrição | Unidade |
| E0 | Sem tensão de carga | V |
| T | Temperatura de operação da célula | K |
| KH2 | Válvula de hidrogênio constante | Kmol.s^(-1) .ATM^(-1) |
| KH2O | Válvula de água constante | Kmol.s^(-1) .ATM^(-1) |
| KO2 | Válvula de oxigênio constante | Kmol.s^(-1) .ATM^(-1) |
| Rho | Razão de fluxo de hidrogênio-oxigênio | - |
| Rint | Resistência interna da célula de combustível | ohm |
| N0 | Número de células | - |
| u | Taxa de utilização de combustível | - |
| I-Start | Cell Operating Current Start Point | UM |
| I-step | Etapa atual de operação de células | UM |
| Eu-Stop | Cell Operating Current End Point | UM |
Model_Name Registro de tela
Modelo estático Amphlett
>>> from opem.Static.Amphlett import Static_Analysis
>>> Test_Vector = { " T " : 343.15 , " PH2 " : 1 , " PO2 " : 1 , " i-start " : 0 , " i-stop " : 75 , " i-step " : 0.1 , " A " : 50.6 , " l " : 0.0178 , " lambda " : 23 , " N " : 1 , " R " : 0 , " JMax " : 1.5 , " Name " : " Amphlett_Test " }
>>> data = Static_Analysis( InputMethod = Test_Vector, TestMode = True , PrintMode = False , ReportMode = False )| Chave | Descrição | Tipo |
| Status | Status da simulação | Bool |
| P | Poder | Lista |
| EU | Corrente operacional de células | Lista |
| V | Tensão FC | Lista |
| Eff | Eficiência | Lista |
| Ph | Energia térmica | Lista |
| V0 | Interceptação linear-apx | Flutuador |
| K | Inclinação linear-apx | Flutuador |
| Eta_active | Ativação do ETA | Lista |
| ETA_CONC | Concentração de ETA | Lista |
| Eta_ohmic | Eta ôhmic | Lista |
| Ve | Tensão estimada de FC | Lista |
Modelo estático Larminie-Dicks
>>> from opem.Static.Larminie_Dicks import Static_Analysis
>>> Test_Vector = { " A " : 0.06 , " E0 " : 1.178 , " T " : 328.15 , " RM " : 0.0018 , " i_0 " : 0.00654 , " i_L " : 100.0 , " i_n " : 0.23 , " N " : 23 , " i-start " : 0.1 , " i-stop " : 98 , " i-step " : 0.1 , " Name " : " Larminiee_Test " }
>>> data = Static_Analysis( InputMethod = Test_Vector, TestMode = True , PrintMode = False , ReportMode = False )| Chave | Descrição | Tipo |
| Status | Status da simulação | Bool |
| P | Poder | Lista |
| EU | Corrente operacional de células | Lista |
| V | Tensão FC | Lista |
| Eff | Eficiência | Lista |
| Ph | Energia térmica | Lista |
| V0 | Interceptação linear-apx | Flutuador |
| K | Inclinação linear-apx | Flutuador |
| Ve | Tensão estimada de FC | Lista |
Modelo estático da Chamberline-Kim
>>> from opem.Static.Chamberline_Kim import Static_Analysis
>>> Test_Vector = { " A " : 50.0 , " E0 " : 0.982 , " b " : 0.0689 , " R " : 0.328 , " m " : 0.000125 , " n " : 9.45 , " N " : 1 , " i-start " : 1 , " i-stop " : 42.5 , " i-step " : 0.1 , " Name " : " Chamberline_Test " }
>>> data = Static_Analysis( InputMethod = Test_Vector, TestMode = True , PrintMode = False , ReportMode = False )| Chave | Descrição | Tipo |
| Status | Status da simulação | Bool |
| P | Poder | Lista |
| EU | Corrente operacional de células | Lista |
| V | Tensão FC | Lista |
| Eff | Eficiência | Lista |
| Ph | Energia térmica | Lista |
| V0 | Interceptação linear-apx | Flutuador |
| K | Inclinação linear-apx | Flutuador |
| Ve | Tensão estimada de FC | Lista |
Padulles Modelo Dinâmico I
>>> from opem.Dynamic.Padulles1 import Dynamic_Analysis
>>> Test_Vector = { " T " : 343 , " E0 " : 0.6 , " N0 " : 88 , " KO2 " : 0.0000211 , " KH2 " : 0.0000422 , " tH2 " : 3.37 , " tO2 " : 6.74 , " B " : 0.04777 , " C " : 0.0136 , " Rint " : 0.00303 , " rho " : 1.168 , " qH2 " : 0.0004 , " i-start " : 0 , " i-stop " : 100 , " i-step " : 0.1 , " Name " : " PadullesI_Test " }
>>> data = Dynamic_Analysis( InputMethod = Test_Vector, TestMode = True , PrintMode = False , ReportMode = False )| Chave | Descrição | Tipo |
| Status | Status da simulação | Bool |
| P | Poder | Lista |
| EU | Corrente operacional de células | Lista |
| V | Tensão FC | Lista |
| Eff | Eficiência | Lista |
| PO2 | Pressão parcial | Lista |
| Ph2 | Pressão parcial | Lista |
| Ph | Energia térmica | Lista |
| V0 | Interceptação linear-apx | Flutuador |
| K | Inclinação linear-apx | Flutuador |
| Ve | Tensão estimada de FC | Lista |
Padulles Dynamic Modelo II
>>> from opem.Dynamic.Padulles2 import Dynamic_Analysis
>>> Test_Vector = { " T " : 343 , " E0 " : 0.6 , " N0 " : 5 , " KO2 " : 0.0000211 , " KH2 " : 0.0000422 , " KH2O " : 0.000007716 , " tH2 " : 3.37 , " tO2 " : 6.74 , " tH2O " : 18.418 , " B " : 0.04777 , " C " : 0.0136 , " Rint " : 0.00303 , " rho " : 1.168 , " qH2 " : 0.0004 , " i-start " : 0.1 , " i-stop " : 100 , " i-step " : 0.1 , " Name " : " Padulles2_Test " }
>>> data = Dynamic_Analysis( InputMethod = Test_Vector, TestMode = True , PrintMode = False , ReportMode = False )| Chave | Descrição | Tipo |
| Status | Status da simulação | Bool |
| P | Poder | Lista |
| EU | Corrente operacional de células | Lista |
| V | Tensão FC | Lista |
| Eff | Eficiência | Lista |
| PO2 | Pressão parcial | Lista |
| Ph2 | Pressão parcial | Lista |
| Ph2O | Pressão parcial | Lista |
| Ph | Energia térmica | Lista |
| V0 | Interceptação linear-apx | Flutuador |
| K | Inclinação linear-apx | Flutuador |
| Ve | Tensão estimada de FC | Lista |
Modelo dinâmico de Padulles-Hauer
>>> from opem.Dynamic.Padulles_Hauer import Dynamic_Analysis
>>> Test_Vector = { " T " : 343 , " E0 " : 0.6 , " N0 " : 5 , " KO2 " : 0.0000211 , " KH2 " : 0.0000422 , " KH2O " : 0.000007716 , " tH2 " : 3.37 , " tO2 " : 6.74 , " t1 " : 2 , " t2 " : 2 , " tH2O " : 18.418 , " B " : 0.04777 , " C " : 0.0136 , " Rint " : 0.00303 , " rho " : 1.168 , " qMethanol " : 0.0002 , " CV " : 2 , " i-start " : 0.1 , " i-stop " : 100 , " i-step " : 0.1 , " Name " : " Padulles_Hauer_Test " }
>>> data = Dynamic_Analysis( InputMethod = Test_Vector, TestMode = True , PrintMode = False , ReportMode = False )| Chave | Descrição | Tipo |
| Status | Status da simulação | Bool |
| P | Poder | Lista |
| EU | Corrente operacional de células | Lista |
| V | Tensão FC | Lista |
| Eff | Eficiência | Lista |
| PO2 | Pressão parcial | Lista |
| Ph2 | Pressão parcial | Lista |
| Ph2O | Pressão parcial | Lista |
| Ph | Energia térmica | Lista |
| V0 | Interceptação linear-apx | Flutuador |
| K | Inclinação linear-apx | Flutuador |
| Ve | Tensão estimada de FC | Lista |
Modelo dinâmico de Padulles-Aprhlett
>>> from opem.Dynamic.Padulles_Amphlett import Dynamic_Analysis
>>> Test_Vector = { " A " : 50.6 , " l " : 0.0178 , " lambda " : 23 , " JMax " : 1.5 , " T " : 343 , " N0 " : 5 , " KO2 " : 0.0000211 , " KH2 " : 0.0000422 , " KH2O " : 0.000007716 , " tH2 " : 3.37 , " tO2 " : 6.74 , " t1 " : 2 , " t2 " : 2 , " tH2O " : 18.418 , " rho " : 1.168 , " qMethanol " : 0.0002 , " CV " : 2 , " i-start " : 0.1 , " i-stop " : 75 , " i-step " : 0.1 , " Name " : " Padulles_Amphlett_Test " }
>>> data = Dynamic_Analysis( InputMethod = Test_Vector, TestMode = True , PrintMode = False , ReportMode = False )| Chave | Descrição | Tipo |
| Status | Status da simulação | Bool |
| P | Poder | Lista |
| EU | Corrente operacional de células | Lista |
| V | Tensão FC | Lista |
| Eff | Eficiência | Lista |
| PO2 | Pressão parcial | Lista |
| Ph2 | Pressão parcial | Lista |
| Ph2O | Pressão parcial | Lista |
| Ph | Energia térmica | Lista |
| V0 | Interceptação linear-apx | Flutuador |
| K | Inclinação linear-apx | Flutuador |
| Eta_active | Ativação do ETA | Lista |
| ETA_CONC | Concentração de ETA | Lista |
| Eta_ohmic | Eta ôhmic | Lista |
| Ve | Tensão estimada de FC | Lista |
Modelo dinâmico de Chakraborty
>>> from opem.Dynamic.Chakraborty import Dynamic_Analysis
>>> Test_Vector = { " T " : 1273 , " E0 " : 0.6 , " u " : 0.8 , " N0 " : 1 , " R " : 3.28125 * 10 ** ( - 3 ), " KH2O " : 0.000281 , " KH2 " : 0.000843 , " KO2 " : 0.00252 , " rho " : 1.145 , " i-start " : 0.1 , " i-stop " : 300 , " i-step " : 0.1 , " Name " : " Chakraborty_Test " }
>>> data = Dynamic_Analysis( InputMethod = Test_Vector, TestMode = True , PrintMode = False , ReportMode = False )| Chave | Descrição | Tipo |
| Status | Status da simulação | Bool |
| P | Poder | Lista |
| EU | Corrente operacional de células | Lista |
| V | Tensão FC | Lista |
| Eff | Eficiência | Lista |
| PO2 | Pressão parcial | Lista |
| Ph2 | Pressão parcial | Lista |
| Ph2O | Pressão parcial | Lista |
| Ph | Energia térmica | Lista |
| Ganho de Nernsnst | Ganho de Nernsnst | Lista |
| Perda ôhmica | Perda ôhmica | Lista |
| V0 | Interceptação linear-apx | Flutuador |
| K | Inclinação linear-apx | Flutuador |
| Ve | Tensão estimada de FC | Lista |
TestMode : Modo de teste ativo e dados de retorno/retorno como dict , (padrão: False )ReportMode : gerar relatórios ( .csv , .opem , .html ) e imprimir resultado em console (padrão: True )PrintMode : Control Printing in Console, (padrão: True )Folder : pasta relatórios, (padrão: os.getcwd() ) dict/start Comando para Opem BotO OPEM pode ser usado online em notebooks interativos de Jupyter através do serviço Binder! Experimente agora! :
.ipynb na pasta DocumentsTest_Vector na seção Full Run Basta preencher um problema e descrevê -lo. Vamos verificar o mais rápido possível! ou envie um email para [email protected].
Você também pode se juntar ao nosso servidor Discord
1- JC Amphlett, RM Baumert, RF Mann, Ba Peppley e PR Roberge. 1995. "Modelagem de desempenho da célula de combustível de eletrólito de polímero sólido Ballard Mark IV". J. Electrochem. Soc. (The Eletroquímica Society, Inc.) 142 (1): 9-15. doi: 10.1149/1.2043959.
2- Jefeson M. Correa, Felix A. Farret, Vladimir A. Popov, Marcelo G. Simoes. 2005. "Análise de sensibilidade dos parâmetros de modelagem usados na simulação de células de combustível de membrana de troca de prótons". IEEE Transações sobre conversão de energia (IEEE) 20 (1): 211-218. doi: 10.1109/tec.2004.842382.
3- Junbom Kim, Seong-Min Lee, supramaniam Srinivasan, Charles E. Chamberlin. 1995. "Modelagem do desempenho das células de combustível da membrana de troca de prótons com uma equação empírica". Jornal da Sociedade Eletroquímica (Sociedade Eletroquímica) 142 (8): 2670-2674. doi: 10.1149/1.2050072.
4- I. Sadli, P. Thounthong, J.-P. Martin, S. Rael, B. Davat. 2006. "Comportamento de um PEMFC que fornece um conversor estático de baixa tensão". Journal of Power Fontes (Elsevier) 156: 119–125. doi: 10.1016/j.jpowsour.2005.08.021.
5- J. Padulles, GW Ault, Jr McDonald. 2000. "Um modelo dinâmico integrado de plantas SOFC para simulação de sistemas de energia". Journal of Power Fontes (Elsevier) 86 (1-2): 495-500. doi: 10.1016/s0378-7753 (99) 00430-9.
6- Hauer, K.-H. 2001. "Ferramenta de análise para hardware e software de veículos de células de combustível (controles) com uma aplicação para comparações de economia de combustível de projetos de sistemas alternativos". Ph.D. Dissertação, Tecnologia e Política de Transporte, Universidade da Califórnia Davis.
7- A. Saadi, M. Becherif, A. Aboubou, meu ayad. 2013. "Comparação dos modelos estáticos de células de combustível da membrana de troca de prótons". Energia renovável (Elsevier) 56: 64-71. doi: dx.doi.org/10.1016/j.renene.2012.10.012.
8- Diego Feroldi, Marta Basualdo. 2012. "Descrição do sistema de células de combustível PEM". Energia e tecnologia verde (Springer) 49-72. doi: 10.1007/978-1-84996-184-4_2
9- Gottesfeld, Shimshon. e a célula de combustível de eletrólito de polímero: problemas de materiais em uma fonte de energia alimentada por hidrogênio. http://physics.oregonstate.edu/~hetheriw/energy/topics/doc/electrochemistry/fc/basic/the_polymer_electrolyte_fuel_cell.htm
10- Mohamed Becherif, Aïcha Saadi, Daniel Hissel, Abdennacer Aboubou, Mohamed Yacine Ayad. 2011. "Modelos de células de combustível de membrana de troca de prótons estáticos e dinâmicos". Journal of Hydrocarbons Mines and Environmental Research 2 (1)
11- Larminie, J., Dicks, A., & McDonald, MS 2003. Sistemas de células de combustível explicadas (Vol. 2, pp. 207-225). Chichester, Reino Unido: J. Wiley. doi: 10.1002/9781118706992.
12- Rho, YW, Srinivasan, S., & Kho, YT 1994. Análise teórica. doi: 10.1149/1.2055066.
13- U. Chakraborty, um novo modelo para utilização constante de combustível e fluxo de combustível constante em células de combustível, Appl. Sci. 9 (2019) 1066. Https://doi.org/10.3390/app9061066.
Se você usa o OPEM em sua pesquisa, cite este artigo:
@article {haghighi2018,
doi = {10.21105/joss.00676},
url = {https://doi.org/10.21105/joss.00676},
ano = {2018},
mês = {jul},
editor = {The Open Journal},
volume = {3},
número = {27},
páginas = {676},
Autor = {Sepand Haghighi e Kasra Askari e Sarmin Hamidi e Mohammad Mahdi Rahimi},
title = {{opem}: Open Source {PEM} Ferramenta de simulação de células},
Journal = {Journal of Open Source Software}
}
Download Opem.bib (formato Bibtex)
| Joss | |
| Zenodo |
Dê a um ️ se este projeto o ajudar!
Se você gosta do nosso projeto e esperamos que você goste, pode nos apoiar? Nosso projeto não é e nunca estará trabalhando com fins lucrativos. Precisamos do dinheiro apenas para que possamos continuar fazendo o que fazemos ;-).