opemダウンロードopemソースコードのダウンロード

opem

その他のカテゴリー

Version 1.4

ダウンロード

PEMとは何ですか？
概要
インストール
使用法
- 実行可能
- 図書館
- 電報ボット
- ブラウザでOPEMを試してみてください！
- マトラブ
問題とバグレポート
貢献
出力
ありがとう
参照
引用
著者
ライセンス
あなたのサポートを見せてください
Changelog
行動規範

概要

プロトン交換膜燃料電池（PEMFC）のモデリングとシミュレーションは、再生可能エネルギー源の研究開発において強力なツールとして機能する可能性があります。オープンソースPEMFCシミュレーションツール（OPEM）は、プロトン交換膜燃料電池の性能を評価するためのモデリングツールです。このパッケージは、PEMFCの最適な動作パラメーターを予測するモデル（静的/動的）の組み合わせです。 OPEMには、入力として受け入れる一般的なモデルが含まれていました。アノードやカソード供給ガス、圧力と組成、細胞温度と電流密度などの動作変数の値だけでなく、活性領域や膜の厚さを含む細胞パラメーターも含まれていました。さらに、OPEMで提案されているPEMFCの異なるモデルのいくつかは、特定のFCスタックに焦点を当てているだけであり、他の一部は改革者などの一部またはすべての補助を考慮に入れています。 OPEMは、PEMFCモデルの共同開発のためのプラットフォームです。

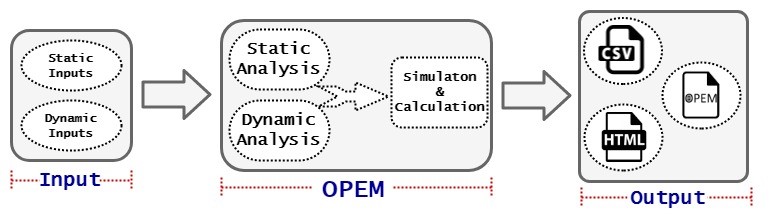
図1。 OPEMブロック図

ハブを開きます
ピピカウンター
Github Stars

支店	マスター	開発する
CI

コード品質

使用法

実行可能

CMD （Windows）またはTerminal （UNIX）を開く
opemまたはpython -m opem （またはOPEM.exeを実行）を実行する

PEMセルパラメーターを入力します（または標準テストベクトルを実行します）

Amphlett静的モデル

入力	説明	ユニット
t	細胞動作温度	k
PH2	部分圧力	ATM
PO2	部分圧力	ATM
私はスタートします	セル動作電流開始点	a
私はステップ	細胞動作電流ステップ	a
istop	細胞動作電流エンドポイント	a
a	アクティブエリア	cm^2
l	膜の厚さ	cm
ラムダ	最小値が14、最大値は23の調整可能なパラメーター	-
r（*オプション）	R-電子	オーム
jmax	最大電流密度	a/（cm^2）
n	単一セルの数	-

*このモデルの詳細については、こちらをご覧ください

Larminie-Dicks静的モデル

入力	説明	ユニット
E0	燃料電池可逆的な損失電圧なし	v
a	タフェル線の勾配	v
t	細胞動作温度	k
私はスタートします	セル動作電流開始点	a
私はステップ	細胞動作電流ステップ	a
istop	細胞動作電流エンドポイント	a
で	内部電流	a
I_0	過電圧がゼロから移動し始める交換電流	a
I_L	電流を制限します	a
rm	膜と接触抵抗	オーム
n	単一セルの数	-

*このモデルの詳細については、こちらをご覧ください

Chamberline-Kim静的モデル

入力	説明	ユニット
E0	開回路電圧	v
b	酸素還元のためのTafelのパラメーター	v
r	抵抗	ohm.cm^2
私はスタートします	セル動作電流開始点	a
私はステップ	細胞動作電流ステップ	a
istop	細胞動作電流エンドポイント	a
a	アクティブエリア	cm^2
m	拡散のパラメーター	v
n	拡散のパラメーター	（a^-1）（cm^2）
n	単一セルの数	-

*このモデルの詳細については、こちらをご覧ください

Padulles動的モデルi

入力	説明	ユニット
E0	負荷電圧はありません	v
t	燃料電池温度	k
KH2	水素バルブ定数	kmol.s^（-1）.atm^（ - 1）
KO2	酸素バルブ定数	kmol.s^（-1）.atm^（ - 1）
Th2	水素時定数	s
to2	酸素時定数	s
b	活性化電圧定数	v
c	アクティベーション定数パラメーター	a^（-1）
リント	燃料電池の内部抵抗	オーム
rho	水素酸素流量比	-
QH2	水素のモル流	kmol/s
N0	セル数	-
私はスタートします	セル動作電流開始点	a
私はステップ	細胞動作電流ステップ	a
istop	細胞動作電流エンドポイント	a

*このモデルの詳細については、こちらをご覧ください

Padulles動的モデルII

入力	説明	ユニット
E0	負荷電圧はありません	v
t	燃料電池温度	k
KH2	水素バルブ定数	kmol.s^（-1）.atm^（ - 1）
KH2O	水バルブ定数	kmol.s^（-1）.atm^（ - 1）
KO2	酸素バルブ定数	kmol.s^（-1）.atm^（ - 1）
Th2	水素時定数	s
Th2o	水時間定数	s
to2	酸素時定数	s
b	活性化電圧定数	v
c	アクティベーション定数パラメーター	a^（-1）
リント	燃料電池の内部抵抗	オーム
rho	水素酸素流量比	-
QH2	水素のモル流	kmol/s
N0	セル数	-
私はスタートします	セル動作電流開始点	a
私はステップ	細胞動作電流ステップ	a
istop	細胞動作電流エンドポイント	a

*このモデルの詳細については、こちらをご覧ください

Padulles-Hauerダイナミックモデル

入力	説明	ユニット
E0	負荷電圧はありません	v
t	燃料電池温度	k
KH2	水素バルブ定数	kmol.s^（-1）.atm^（ - 1）
KH2O	水バルブ定数	kmol.s^（-1）.atm^（ - 1）
KO2	酸素バルブ定数	kmol.s^（-1）.atm^（ - 1）
Th2	水素時定数	s
Th2o	水時間定数	s
to2	酸素時定数	s
T1	改革者の時定数	s
T2	改革者の時定数	s
b	活性化電圧定数	v
c	アクティベーション定数パラメーター	a^（-1）
cv	変換係数	-
リント	燃料電池の内部抵抗	オーム
rho	水素酸素流量比	-
qmethanol	メタノールのモル流	kmol/s
N0	セル数	-
私はスタートします	セル動作電流開始点	a
私はステップ	細胞動作電流ステップ	a
istop	細胞動作電流エンドポイント	a

*このモデルの詳細については、こちらをご覧ください

Padulles-Amphlettダイナミックモデル

入力	説明	ユニット
E0	負荷電圧はありません	v
t	燃料電池温度	k
KH2	水素バルブ定数	kmol.s^（-1）.atm^（ - 1）
KH2O	水バルブ定数	kmol.s^（-1）.atm^（ - 1）
KO2	酸素バルブ定数	kmol.s^（-1）.atm^（ - 1）
Th2	水素時定数	s
Th2o	水時間定数	s
to2	酸素時定数	s
T1	改革者の時定数	s
T2	改革者の時定数	s
a	アクティブエリア	cm^2
l	膜の厚さ	cm
ラムダ	最小値が14、最大値は23の調整可能なパラメーター	-
r（*オプション）	R-電子	オーム
jmax	最大電流密度	a/（cm^2）
cv	変換係数	-
rho	水素酸素流量比	-
qmethanol	メタノールのモル流	kmol/s
N0	セル数	-
私はスタートします	セル動作電流開始点	a
私はステップ	細胞動作電流ステップ	a
istop	細胞動作電流エンドポイント	a

*このモデルの詳細については、こちらをご覧ください

Chakrabortyダイナミックモデル

入力	説明	ユニット
E0	負荷電圧はありません	v
t	細胞動作温度	k
KH2	水素バルブ定数	kmol.s^（-1）.atm^（ - 1）
KH2O	水バルブ定数	kmol.s^（-1）.atm^（ - 1）
KO2	酸素バルブ定数	kmol.s^（-1）.atm^（ - 1）
rho	水素酸素流量比	-
リント	燃料電池の内部抵抗	オーム
N0	セル数	-
u	燃料利用率	-
私はスタートします	セル動作電流開始点	a
私はステップ	細胞動作電流ステップ	a
istop	細胞動作電流エンドポイント	a

*このモデルの詳細については、こちらをご覧ください

Model_Nameフォルダーでレポートを見つけます

スクリーンレコード

図書館

Amphlett静的モデル

>>> from opem.Static.Amphlett import Static_Analysis
>>> Test_Vector = { " T " : 343.15 , " PH2 " : 1 , " PO2 " : 1 , " i-start " : 0 , " i-stop " : 75 , " i-step " : 0.1 , " A " : 50.6 , " l " : 0.0178 , " lambda " : 23 , " N " : 1 , " R " : 0 , " JMax " : 1.5 , " Name " : " Amphlett_Test " }
>>> data = Static_Analysis( InputMethod = Test_Vector, TestMode = True , PrintMode = False , ReportMode = False )

鍵	説明	タイプ
状態	シミュレーションステータス	ブール
p	力	リスト
私	細胞動作電流	リスト
v	FC電圧	リスト
Eff	効率	リスト
ph	熱電力	リスト
V0	線形APXインターセプト	フロート
k	線形-APXスロープ	フロート
ETA_ACTIVE	ETA活性化	リスト
ETA_CONC	ETA濃度	リスト
ETA_OHMIC	eta ohmic	リスト
ve	推定FC電圧	リスト

このモデルの詳細については、こちらをご覧ください

Larminie-Dicks静的モデル

>>> from opem.Static.Larminie_Dicks import Static_Analysis
>>> Test_Vector = { " A " : 0.06 , " E0 " : 1.178 , " T " : 328.15 , " RM " : 0.0018 , " i_0 " : 0.00654 , " i_L " : 100.0 , " i_n " : 0.23 , " N " : 23 , " i-start " : 0.1 , " i-stop " : 98 , " i-step " : 0.1 , " Name " : " Larminiee_Test " }
>>> data = Static_Analysis( InputMethod = Test_Vector, TestMode = True , PrintMode = False , ReportMode = False )

鍵	説明	タイプ
状態	シミュレーションステータス	ブール
p	力	リスト
私	細胞動作電流	リスト
v	FC電圧	リスト
Eff	効率	リスト
ph	熱電力	リスト
V0	線形APXインターセプト	フロート
k	線形-APXスロープ	フロート
ve	推定FC電圧	リスト

このモデルの詳細については、こちらをご覧ください

Chamberline-Kim静的モデル

>>> from opem.Static.Chamberline_Kim import Static_Analysis
>>> Test_Vector = { " A " : 50.0 , " E0 " : 0.982 , " b " : 0.0689 , " R " : 0.328 , " m " : 0.000125 , " n " : 9.45 , " N " : 1 , " i-start " : 1 , " i-stop " : 42.5 , " i-step " : 0.1 , " Name " : " Chamberline_Test " }
>>> data = Static_Analysis( InputMethod = Test_Vector, TestMode = True , PrintMode = False , ReportMode = False )

鍵	説明	タイプ
状態	シミュレーションステータス	ブール
p	力	リスト
私	細胞動作電流	リスト
v	FC電圧	リスト
Eff	効率	リスト
ph	熱電力	リスト
V0	線形APXインターセプト	フロート
k	線形-APXスロープ	フロート
ve	推定FC電圧	リスト

このモデルの詳細については、こちらをご覧ください

Padulles動的モデルi

>>> from opem.Dynamic.Padulles1 import Dynamic_Analysis
>>> Test_Vector = { " T " : 343 , " E0 " : 0.6 , " N0 " : 88 , " KO2 " : 0.0000211 , " KH2 " : 0.0000422 , " tH2 " : 3.37 , " tO2 " : 6.74 , " B " : 0.04777 , " C " : 0.0136 , " Rint " : 0.00303 , " rho " : 1.168 , " qH2 " : 0.0004 , " i-start " : 0 , " i-stop " : 100 , " i-step " : 0.1 , " Name " : " PadullesI_Test " }
>>> data = Dynamic_Analysis( InputMethod = Test_Vector, TestMode = True , PrintMode = False , ReportMode = False )

鍵	説明	タイプ
状態	シミュレーションステータス	ブール
p	力	リスト
私	細胞動作電流	リスト
v	FC電圧	リスト
Eff	効率	リスト
PO2	部分圧力	リスト
PH2	部分圧力	リスト
ph	熱電力	リスト
V0	線形APXインターセプト	フロート
k	線形-APXスロープ	フロート
ve	推定FC電圧	リスト

このモデルの詳細については、こちらをご覧ください

Padulles動的モデルII

>>> from opem.Dynamic.Padulles2 import Dynamic_Analysis
>>> Test_Vector = { " T " : 343 , " E0 " : 0.6 , " N0 " : 5 , " KO2 " : 0.0000211 , " KH2 " : 0.0000422 , " KH2O " : 0.000007716 , " tH2 " : 3.37 , " tO2 " : 6.74 , " tH2O " : 18.418 , " B " : 0.04777 , " C " : 0.0136 , " Rint " : 0.00303 , " rho " : 1.168 , " qH2 " : 0.0004 , " i-start " : 0.1 , " i-stop " : 100 , " i-step " : 0.1 , " Name " : " Padulles2_Test " }
>>> data = Dynamic_Analysis( InputMethod = Test_Vector, TestMode = True , PrintMode = False , ReportMode = False )

鍵	説明	タイプ
状態	シミュレーションステータス	ブール
p	力	リスト
私	細胞動作電流	リスト
v	FC電圧	リスト
Eff	効率	リスト
PO2	部分圧力	リスト
PH2	部分圧力	リスト
ph2o	部分圧力	リスト
ph	熱電力	リスト
V0	線形APXインターセプト	フロート
k	線形-APXスロープ	フロート
ve	推定FC電圧	リスト

このモデルの詳細については、こちらをご覧ください

Padulles-Hauerダイナミックモデル

>>> from opem.Dynamic.Padulles_Hauer import Dynamic_Analysis
>>> Test_Vector = { " T " : 343 , " E0 " : 0.6 , " N0 " : 5 , " KO2 " : 0.0000211 , " KH2 " : 0.0000422 , " KH2O " : 0.000007716 , " tH2 " : 3.37 , " tO2 " : 6.74 , " t1 " : 2 , " t2 " : 2 , " tH2O " : 18.418 , " B " : 0.04777 , " C " : 0.0136 , " Rint " : 0.00303 , " rho " : 1.168 , " qMethanol " : 0.0002 , " CV " : 2 , " i-start " : 0.1 , " i-stop " : 100 , " i-step " : 0.1 , " Name " : " Padulles_Hauer_Test " }
>>> data = Dynamic_Analysis( InputMethod = Test_Vector, TestMode = True , PrintMode = False , ReportMode = False )

鍵	説明	タイプ
状態	シミュレーションステータス	ブール
p	力	リスト
私	細胞動作電流	リスト
v	FC電圧	リスト
Eff	効率	リスト
PO2	部分圧力	リスト
PH2	部分圧力	リスト
ph2o	部分圧力	リスト
ph	熱電力	リスト
V0	線形APXインターセプト	フロート
k	線形-APXスロープ	フロート
ve	推定FC電圧	リスト

このモデルの詳細については、こちらをご覧ください

Padulles-Amphlettダイナミックモデル

>>> from opem.Dynamic.Padulles_Amphlett import Dynamic_Analysis
>>> Test_Vector = { " A " : 50.6 , " l " : 0.0178 , " lambda " : 23 , " JMax " : 1.5 , " T " : 343 , " N0 " : 5 , " KO2 " : 0.0000211 , " KH2 " : 0.0000422 , " KH2O " : 0.000007716 , " tH2 " : 3.37 , " tO2 " : 6.74 , " t1 " : 2 , " t2 " : 2 , " tH2O " : 18.418 , " rho " : 1.168 , " qMethanol " : 0.0002 , " CV " : 2 , " i-start " : 0.1 , " i-stop " : 75 , " i-step " : 0.1 , " Name " : " Padulles_Amphlett_Test " }
>>> data = Dynamic_Analysis( InputMethod = Test_Vector, TestMode = True , PrintMode = False , ReportMode = False )

鍵	説明	タイプ
状態	シミュレーションステータス	ブール
p	力	リスト
私	細胞動作電流	リスト
v	FC電圧	リスト
Eff	効率	リスト
PO2	部分圧力	リスト
PH2	部分圧力	リスト
ph2o	部分圧力	リスト
ph	熱電力	リスト
V0	線形APXインターセプト	フロート
k	線形-APXスロープ	フロート
ETA_ACTIVE	ETA活性化	リスト
ETA_CONC	ETA濃度	リスト
ETA_OHMIC	eta ohmic	リスト
ve	推定FC電圧	リスト

このモデルの詳細については、こちらをご覧ください

Chakrabortyダイナミックモデル

>>> from opem.Dynamic.Chakraborty import Dynamic_Analysis
>>> Test_Vector = { " T " : 1273 , " E0 " : 0.6 , " u " : 0.8 , " N0 " : 1 , " R " : 3.28125 * 10 ** ( - 3 ), " KH2O " : 0.000281 , " KH2 " : 0.000843 , " KO2 " : 0.00252 , " rho " : 1.145 , " i-start " : 0.1 , " i-stop " : 300 , " i-step " : 0.1 , " Name " : " Chakraborty_Test " }
>>> data = Dynamic_Analysis( InputMethod = Test_Vector, TestMode = True , PrintMode = False , ReportMode = False )

鍵	説明	タイプ
状態	シミュレーションステータス	ブール
p	力	リスト
私	細胞動作電流	リスト
v	FC電圧	リスト
Eff	効率	リスト
PO2	部分圧力	リスト
PH2	部分圧力	リスト
ph2o	部分圧力	リスト
ph	熱電力	リスト
ネルンストゲイン	ネルンストゲイン	リスト
オーム損失	オーム損失	リスト
V0	線形APXインターセプト	フロート
k	線形-APXスロープ	フロート
ve	推定FC電圧	リスト

このモデルの詳細については、こちらをご覧ください

パラメーター

TestMode ：アクティブなテストモードとdictとしてデータを取得/返す（デフォルト： False ）
ReportMode ：レポート（ .csv 、 .opem 、 .html ）を生成し、コンソールを印刷します（デフォルト： True ）
PrintMode ：コンソールでの制御印刷、（デフォルト： True ）
Folder ：レポートフォルダー（デフォルト： os.getcwd() ）

注記

戻りタイプ： dict

電報ボット

OPEMボットにコマンドを送信/start
メニューからモデルを選択します
テンプレートに従ってテストベクトルを送信します
結果をダウンロードしてください

ブラウザでOPEMを試してみてください！

OPEMは、バインダーサービスを介してインタラクティブなJupyterノートブックでオンラインで使用できます！今すぐ試してみてください！：

Documentsフォルダーの.ipynbファイルを確認してください
ノートの各部分を編集して実行し、実行ボタンで上部パネルから段階的に段階的に実行します
完全なシミュレーションを実行するには、 Full RunセクションでTest_Vectorを編集できます

問題とバグレポート

問題を記入して説明してください。できるだけ早くチェックします！または、[email protected]にメールを送信します。

Discordサーバーに参加することもできます

出力

HTML
CSV
Opem

ありがとう

chart.js
pyinstaller
draw.io
Zahra Mobasher（ロゴデザイン）

参照

1- JC Amphlett、RM Baumert、RF Mann、Ba Peppley、およびPr Roberge。 1995年。「バラードマークIVソリッドポリマー電解質燃料電池の性能モデリング。 J. Electrochem。 Soc。（The Electrochemical Society、Inc。）142（1）：9-15。 doi：10.1149/1.2043959。

2-ジェファーソンM.コレア、フェリックスA.ファレット、ウラジミールA.ポポフ、マルセロG.シモエス。 2005。「プロトン交換膜燃料電池のシミュレーションで使用されるモデリングパラメーターの感度分析。」エネルギー変換に関するIEEEトランザクション（IEEE）20（1）：211-218。 doi：10.1109/tec.2004.842382。

3- Junbom Kim、Seong-Min Lee、Supramaniam Srinivasan、Charles E. Chamberlin。 1995。 Journal of the Electrochemical Society（The Electrochemical Society）142（8）：2670-2674。 doi：10.1149/1.2050072。

4- I. Sadli、P。Thounthong、J.P。マーティン、S。レール、B。ダバット。 2006年。「低電圧静的コンバーターを供給するPEMFCの動作。」 Journal of Power Sources（Elsevier）156：119–125。 doi：10.1016/j.jpowsour.2005.08.021。

5- J. Padulles、GW Ault、Jr McDonald。 2000。 Journal of Power Sources（Elsevier）86（1-2）：495-500。 doi：10.1016/s0378-7753（99）00430-9。

6-ハウアー、K.-H。 2001。「燃料電池車両ハードウェアとソフトウェア（コントロール）の分析ツール。代替システム設計の燃費比較へのアプリケーション。」博士号論文、交通技術と政策、カリフォルニア大学デイビス校。

7- A. Saadi、M。Becherif、A。Aboubou、私のAyad。 2013。「陽子交換膜燃料電池静的モデルの比較。」再生可能エネルギー（エルゼビア）56：64-71。 doi：dx.doi.org/10.1016/j.renene.2012.10.012。

8-ディエゴ・フェロルディ、マルタ・バシュアルド。 2012年。「PEM燃料電池システムの説明。」 Green Energy and Technology（Springer）49-72。 doi：10.1007/978-1-84996-184-4_2

9-ゴッテスフェルド、シムショーン。 ndポリマー電解質燃料電池：水素燃料供給源の材料の問題。 http://physics.oregonstate.edu/~hetheriw/energy/topics/doc/electrochemistry/fc/basic/the_polymer_electrololyte_fuel_cell.htm

10-モハメド・ベチェリフ、アイチャ・サーディ、ダニエル・ヒスセル、アブデンナーサー・アブブー、モハメド・ヤシン・アヤド。 2011。「静的および動的陽子交換膜燃料電池モデル」。 Journal of Hydrocarbons Mines and Environmental Research 2（1）

11- Larminie、J.、Dicks、A。、＆McDonald、MS2003。FuelCell Systems Adeased（Vol。2、pp。207-225）。英国チチェスター：J。ワイリー。 doi：10.1002/9781118706992。

12- Rho、YW、Srinivasan、S。、＆Kho、YT 1994。 '' O 2/HE、O 2/AR、およびO 2/N 2混合物を使用したプロトン交換膜燃料電池における大量輸送現象II。理論分析。 '' Journal of the Electrochemical Society、141（8）、2089-2096。 doi：10.1149/1.2055066。

13- U. Chakraborty、燃料電池の一定の燃料利用と一定の燃料流の新しいモデル、Appl。 SCI。 9（2019）1066。https：//doi.org/10.3390/App9061066。

引用

研究でOPEMを使用している場合は、この論文を引用してください。

 @article {haghighi2018、
  doi = {10.21105/joss.00676}、
  url = {https://doi.org/10.21105/joss.00676}、
  year = {2018}、
  月= {7月}、
  Publisher = {The Open Journal}、
  volume = {3}、
  番号= {27}、
  ページ= {676}、
  著者= {sepand haghighiとKasra askariとSarmin HamidiとMohammad Mahdi Rahimi}、
  title = {{opem}：open source {pem}セルシミュレーションツール}、
  Journal = {Journal of Open Source Software}
}

opem.bib（bibtex形式）をダウンロード