opem 다운로드 - opem 소스 코드 다운로드

opem

기타 카테고리

Version 1.4

다운로드

개요

양성자 교환 막 연료 전지 (PEMFC)의 모델링 및 시뮬레이션은 재생 가능한 에너지 원의 연구 및 개발에서 강력한 도구로 작용할 수 있습니다. 오픈 소스 PEMFC 시뮬레이션 도구 (OPEM)는 양성자 교환 막 연료 전지의 성능을 평가하기위한 모델링 도구입니다. 이 패키지는 PEMFC의 최적 작동 매개 변수를 예측하는 모델 (정적/동적)의 조합입니다. OPEM에는 양극 및 음극 공급 가스, 압력 및 조성물, 세포 온도 및 전류 밀도와 같은 작동 변수의 값뿐만 아니라 활성 영역 및 막 두께를 포함한 셀 파라미터도 입력으로 받아 들일 일반 모델이 포함되어 있습니다. 또한, OPEM에서 제안 된 PEMFC의 다른 모델 중 일부는 하나의 특정 FC 스택에 중점을두고 일부는 개혁자와 같은 일부 또는 모든 보조 장치를 고려합니다. OPEM은 PEMFC 모델의 공동 개발을위한 플랫폼입니다.

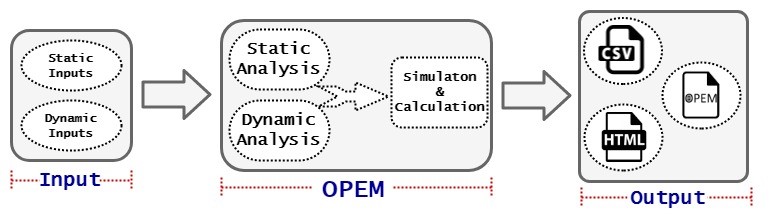
그림 1. OPEM 블록 다이어그램

오픈 허브
PYPI 카운터
Github 스타

나뭇가지	주인	개발하다
CI

코드 품질

용법

실행 파일

CMD (Windows) 또는 Terminal (UNIX) 열기
opem 또는 python -m opem (또는 OPEM.exe 실행)

PEM 세포 매개 변수를 입력하십시오 (또는 표준 테스트 벡터 실행)

Amphlett 정적 모델

입력	설명	단위
티	셀 작동 온도	케이
ph2	부분 압력	ATM
po2	부분 압력	ATM
I- 스타트	셀 작동 전류 시작점	에이
I 단계	셀 작동 현재 단계	에이
I- 스톱	셀 작동 전류 종료점	에이
에이	활성 영역	cm^2
엘	멤브레인 두께	cm
람다	최소값 14이고 최대 값이 23 인 조정 가능한 매개 변수	-
r (*선택 사항)	R- 전자	옴
Jmax	최대 전류 밀도	a/(cm^2)
N	단일 세포의 수	-

*이 모델에 대한 자세한 내용은 여기를 방문하십시오

Larminie-Dicks 정적 모델

입력	설명	단위
E0	연료 전지 가역적 손실 전압 없음	다섯
에이	Tafel 라인의 경사	다섯
티	셀 작동 온도	케이
I- 스타트	셀 작동 전류 시작점	에이
I 단계	셀 작동 현재 단계	에이
I- 스톱	셀 작동 전류 종료점	에이
안에	내부 전류	에이
i_0	과전압이 0에서 이동하기 시작하는 교환 전류	에이
I_L	전류 제한	에이
Rm	막 및 접촉 저항	옴
N	단일 세포의 수	-

*이 모델에 대한 자세한 내용은 여기를 방문하십시오

Chamberline-Kim 정적 모델

입력	설명	단위
E0	개방 회로 전압	다섯
비	산소 감소를위한 Tafel의 매개 변수	다섯
아르 자형	저항	OHM.CM^2
I- 스타트	셀 작동 전류 시작점	에이
I 단계	셀 작동 현재 단계	에이
I- 스톱	셀 작동 전류 종료점	에이
에이	활성 영역	cm^2
중	확산의 매개 변수	다섯
N	확산의 매개 변수	(a^-1) (cm^2)
N	단일 세포의 수	-

*이 모델에 대한 자세한 내용은 여기를 방문하십시오

Padulles 동적 모델 i

입력	설명	단위
E0	로드 전압이 없습니다	다섯
티	연료 전지 온도	케이
KH2	수소 밸브 상수	kmol.s^(-1) .atm^(-1)
KO2	산소 밸브 상수	kmol.s^(-1) .atm^(-1)
Th2	수소 시간 상수	에스
to2	산소 시간 상수	에스
비	활성화 전압 상수	다섯
기음	활성화 상수 매개 변수	a^(-1)
신장	연료 전지 내부 저항	옴
Rho	수소-산소 흐름 비율	-
QH2	수소의 어금니 흐름	kmol/s
N0	세포 수	-
I- 스타트	셀 작동 전류 시작점	에이
I 단계	셀 작동 현재 단계	에이
I- 스톱	셀 작동 전류 종료점	에이

*이 모델에 대한 자세한 내용은 여기를 방문하십시오

Padulles 동적 모델 II

입력	설명	단위
E0	로드 전압이 없습니다	다섯
티	연료 전지 온도	케이
KH2	수소 밸브 상수	kmol.s^(-1) .atm^(-1)
KH2O	워터 밸브 상수	kmol.s^(-1) .atm^(-1)
KO2	산소 밸브 상수	kmol.s^(-1) .atm^(-1)
Th2	수소 시간 상수	에스
th2o	물 시간 상수	에스
to2	산소 시간 상수	에스
비	활성화 전압 상수	다섯
기음	활성화 상수 매개 변수	a^(-1)
신장	연료 전지 내부 저항	옴
Rho	수소-산소 흐름 비율	-
QH2	수소의 어금니 흐름	kmol/s
N0	세포 수	-
I- 스타트	셀 작동 전류 시작점	에이
I 단계	셀 작동 현재 단계	에이
I- 스톱	셀 작동 전류 종료점	에이

*이 모델에 대한 자세한 내용은 여기를 방문하십시오

Padulles-Hauer 동적 모델

입력	설명	단위
E0	로드 전압이 없습니다	다섯
티	연료 전지 온도	케이
KH2	수소 밸브 상수	kmol.s^(-1) .atm^(-1)
KH2O	워터 밸브 상수	kmol.s^(-1) .atm^(-1)
KO2	산소 밸브 상수	kmol.s^(-1) .atm^(-1)
Th2	수소 시간 상수	에스
th2o	물 시간 상수	에스
to2	산소 시간 상수	에스
T1	개혁자 시간 상수	에스
T2	개혁자 시간 상수	에스
비	활성화 전압 상수	다섯
기음	활성화 상수 매개 변수	a^(-1)
CV	변환 계수	-
신장	연료 전지 내부 저항	옴
Rho	수소-산소 흐름 비율	-
Qmethanol	메탄올의 어금니 흐름	kmol/s
N0	세포 수	-
I- 스타트	셀 작동 전류 시작점	에이
I 단계	셀 작동 현재 단계	에이
I- 스톱	셀 작동 전류 종료점	에이

*이 모델에 대한 자세한 내용은 여기를 방문하십시오

Padulles-Amphlett 동적 모델

입력	설명	단위
E0	로드 전압이 없습니다	다섯
티	연료 전지 온도	케이
KH2	수소 밸브 상수	kmol.s^(-1) .atm^(-1)
KH2O	워터 밸브 상수	kmol.s^(-1) .atm^(-1)
KO2	산소 밸브 상수	kmol.s^(-1) .atm^(-1)
Th2	수소 시간 상수	에스
th2o	물 시간 상수	에스
to2	산소 시간 상수	에스
T1	개혁자 시간 상수	에스
T2	개혁자 시간 상수	에스
에이	활성 영역	cm^2
엘	멤브레인 두께	cm
람다	최소값 14이고 최대 값이 23 인 조정 가능한 매개 변수	-
r (*선택 사항)	R- 전자	옴
Jmax	최대 전류 밀도	a/(cm^2)
CV	변환 계수	-
Rho	수소-산소 흐름 비율	-
Qmethanol	메탄올의 어금니 흐름	kmol/s
N0	세포 수	-
I- 스타트	셀 작동 전류 시작점	에이
I 단계	셀 작동 현재 단계	에이
I- 스톱	셀 작동 전류 종료점	에이

*이 모델에 대한 자세한 내용은 여기를 방문하십시오

차크라보티 동적 모델

입력	설명	단위
E0	로드 전압이 없습니다	다섯
티	셀 작동 온도	케이
KH2	수소 밸브 상수	kmol.s^(-1) .atm^(-1)
KH2O	워터 밸브 상수	kmol.s^(-1) .atm^(-1)
KO2	산소 밸브 상수	kmol.s^(-1) .atm^(-1)
Rho	수소-산소 흐름 비율	-
신장	연료 전지 내부 저항	옴
N0	세포 수	-
유	연료 활용 비율	-
I- 스타트	셀 작동 전류 시작점	에이
I 단계	셀 작동 현재 단계	에이
I- 스톱	셀 작동 전류 종료점	에이

*이 모델에 대한 자세한 내용은 여기를 방문하십시오

Model_Name 폴더에서 보고서를 찾으십시오

스크린 레코드

도서관

Amphlett 정적 모델

>>> from opem.Static.Amphlett import Static_Analysis
>>> Test_Vector = { " T " : 343.15 , " PH2 " : 1 , " PO2 " : 1 , " i-start " : 0 , " i-stop " : 75 , " i-step " : 0.1 , " A " : 50.6 , " l " : 0.0178 , " lambda " : 23 , " N " : 1 , " R " : 0 , " JMax " : 1.5 , " Name " : " Amphlett_Test " }
>>> data = Static_Analysis( InputMethod = Test_Vector, TestMode = True , PrintMode = False , ReportMode = False )

열쇠	설명	유형
상태	시뮬레이션 상태	부
피	힘	목록
나	셀 작동 전류	목록
다섯	FC 전압	목록
Eff	능률	목록
ph	열 전력	목록
V0	선형 -APX 절편	뜨다
케이	선형 -APX 경사	뜨다
eta_active	ETA 활성화	목록
ETA_CONC	ETA 농도	목록
eta_ohmic	Eta Ohmic	목록
ve	추정 FC 전압	목록

이 모델에 대한 자세한 내용은 여기를 방문하십시오

Larminie-Dicks 정적 모델

>>> from opem.Static.Larminie_Dicks import Static_Analysis
>>> Test_Vector = { " A " : 0.06 , " E0 " : 1.178 , " T " : 328.15 , " RM " : 0.0018 , " i_0 " : 0.00654 , " i_L " : 100.0 , " i_n " : 0.23 , " N " : 23 , " i-start " : 0.1 , " i-stop " : 98 , " i-step " : 0.1 , " Name " : " Larminiee_Test " }
>>> data = Static_Analysis( InputMethod = Test_Vector, TestMode = True , PrintMode = False , ReportMode = False )

열쇠	설명	유형
상태	시뮬레이션 상태	부
피	힘	목록
나	셀 작동 전류	목록
다섯	FC 전압	목록
Eff	능률	목록
ph	열 전력	목록
V0	선형 -APX 절편	뜨다
케이	선형 -APX 경사	뜨다
ve	추정 FC 전압	목록

이 모델에 대한 자세한 내용은 여기를 방문하십시오

Chamberline-Kim 정적 모델

>>> from opem.Static.Chamberline_Kim import Static_Analysis
>>> Test_Vector = { " A " : 50.0 , " E0 " : 0.982 , " b " : 0.0689 , " R " : 0.328 , " m " : 0.000125 , " n " : 9.45 , " N " : 1 , " i-start " : 1 , " i-stop " : 42.5 , " i-step " : 0.1 , " Name " : " Chamberline_Test " }
>>> data = Static_Analysis( InputMethod = Test_Vector, TestMode = True , PrintMode = False , ReportMode = False )

열쇠	설명	유형
상태	시뮬레이션 상태	부
피	힘	목록
나	셀 작동 전류	목록
다섯	FC 전압	목록
Eff	능률	목록
ph	열 전력	목록
V0	선형 -APX 절편	뜨다
케이	선형 -APX 경사	뜨다
ve	추정 FC 전압	목록

이 모델에 대한 자세한 내용은 여기를 방문하십시오

Padulles 동적 모델 i

>>> from opem.Dynamic.Padulles1 import Dynamic_Analysis
>>> Test_Vector = { " T " : 343 , " E0 " : 0.6 , " N0 " : 88 , " KO2 " : 0.0000211 , " KH2 " : 0.0000422 , " tH2 " : 3.37 , " tO2 " : 6.74 , " B " : 0.04777 , " C " : 0.0136 , " Rint " : 0.00303 , " rho " : 1.168 , " qH2 " : 0.0004 , " i-start " : 0 , " i-stop " : 100 , " i-step " : 0.1 , " Name " : " PadullesI_Test " }
>>> data = Dynamic_Analysis( InputMethod = Test_Vector, TestMode = True , PrintMode = False , ReportMode = False )

열쇠	설명	유형
상태	시뮬레이션 상태	부
피	힘	목록
나	셀 작동 전류	목록
다섯	FC 전압	목록
Eff	능률	목록
po2	부분 압력	목록
ph2	부분 압력	목록
ph	열 전력	목록
V0	선형 -APX 절편	뜨다
케이	선형 -APX 경사	뜨다
ve	추정 FC 전압	목록

이 모델에 대한 자세한 내용은 여기를 방문하십시오

Padulles 동적 모델 II

>>> from opem.Dynamic.Padulles2 import Dynamic_Analysis
>>> Test_Vector = { " T " : 343 , " E0 " : 0.6 , " N0 " : 5 , " KO2 " : 0.0000211 , " KH2 " : 0.0000422 , " KH2O " : 0.000007716 , " tH2 " : 3.37 , " tO2 " : 6.74 , " tH2O " : 18.418 , " B " : 0.04777 , " C " : 0.0136 , " Rint " : 0.00303 , " rho " : 1.168 , " qH2 " : 0.0004 , " i-start " : 0.1 , " i-stop " : 100 , " i-step " : 0.1 , " Name " : " Padulles2_Test " }
>>> data = Dynamic_Analysis( InputMethod = Test_Vector, TestMode = True , PrintMode = False , ReportMode = False )

열쇠	설명	유형
상태	시뮬레이션 상태	부
피	힘	목록
나	셀 작동 전류	목록
다섯	FC 전압	목록
Eff	능률	목록
po2	부분 압력	목록
ph2	부분 압력	목록
ph2o	부분 압력	목록
ph	열 전력	목록
V0	선형 -APX 절편	뜨다
케이	선형 -APX 경사	뜨다
ve	추정 FC 전압	목록

이 모델에 대한 자세한 내용은 여기를 방문하십시오

Padulles-Hauer 동적 모델

>>> from opem.Dynamic.Padulles_Hauer import Dynamic_Analysis
>>> Test_Vector = { " T " : 343 , " E0 " : 0.6 , " N0 " : 5 , " KO2 " : 0.0000211 , " KH2 " : 0.0000422 , " KH2O " : 0.000007716 , " tH2 " : 3.37 , " tO2 " : 6.74 , " t1 " : 2 , " t2 " : 2 , " tH2O " : 18.418 , " B " : 0.04777 , " C " : 0.0136 , " Rint " : 0.00303 , " rho " : 1.168 , " qMethanol " : 0.0002 , " CV " : 2 , " i-start " : 0.1 , " i-stop " : 100 , " i-step " : 0.1 , " Name " : " Padulles_Hauer_Test " }
>>> data = Dynamic_Analysis( InputMethod = Test_Vector, TestMode = True , PrintMode = False , ReportMode = False )

열쇠	설명	유형
상태	시뮬레이션 상태	부
피	힘	목록
나	셀 작동 전류	목록
다섯	FC 전압	목록
Eff	능률	목록
po2	부분 압력	목록
ph2	부분 압력	목록
ph2o	부분 압력	목록
ph	열 전력	목록
V0	선형 -APX 절편	뜨다
케이	선형 -APX 경사	뜨다
ve	추정 FC 전압	목록

이 모델에 대한 자세한 내용은 여기를 방문하십시오

Padulles-Amphlett 동적 모델

>>> from opem.Dynamic.Padulles_Amphlett import Dynamic_Analysis
>>> Test_Vector = { " A " : 50.6 , " l " : 0.0178 , " lambda " : 23 , " JMax " : 1.5 , " T " : 343 , " N0 " : 5 , " KO2 " : 0.0000211 , " KH2 " : 0.0000422 , " KH2O " : 0.000007716 , " tH2 " : 3.37 , " tO2 " : 6.74 , " t1 " : 2 , " t2 " : 2 , " tH2O " : 18.418 , " rho " : 1.168 , " qMethanol " : 0.0002 , " CV " : 2 , " i-start " : 0.1 , " i-stop " : 75 , " i-step " : 0.1 , " Name " : " Padulles_Amphlett_Test " }
>>> data = Dynamic_Analysis( InputMethod = Test_Vector, TestMode = True , PrintMode = False , ReportMode = False )

열쇠	설명	유형
상태	시뮬레이션 상태	부
피	힘	목록
나	셀 작동 전류	목록
다섯	FC 전압	목록
Eff	능률	목록
po2	부분 압력	목록
ph2	부분 압력	목록
ph2o	부분 압력	목록
ph	열 전력	목록
V0	선형 -APX 절편	뜨다
케이	선형 -APX 경사	뜨다
eta_active	ETA 활성화	목록
ETA_CONC	ETA 농도	목록
eta_ohmic	Eta Ohmic	목록
ve	추정 FC 전압	목록

이 모델에 대한 자세한 내용은 여기를 방문하십시오

차크라보티 동적 모델

>>> from opem.Dynamic.Chakraborty import Dynamic_Analysis
>>> Test_Vector = { " T " : 1273 , " E0 " : 0.6 , " u " : 0.8 , " N0 " : 1 , " R " : 3.28125 * 10 ** ( - 3 ), " KH2O " : 0.000281 , " KH2 " : 0.000843 , " KO2 " : 0.00252 , " rho " : 1.145 , " i-start " : 0.1 , " i-stop " : 300 , " i-step " : 0.1 , " Name " : " Chakraborty_Test " }
>>> data = Dynamic_Analysis( InputMethod = Test_Vector, TestMode = True , PrintMode = False , ReportMode = False )

열쇠	설명	유형
상태	시뮬레이션 상태	부
피	힘	목록
나	셀 작동 전류	목록
다섯	FC 전압	목록
Eff	능률	목록
po2	부분 압력	목록
ph2	부분 압력	목록
ph2o	부분 압력	목록
ph	열 전력	목록
Nernst Gain	Nernst Gain	목록
옴 손실	옴 손실	목록
V0	선형 -APX 절편	뜨다
케이	선형 -APX 경사	뜨다
ve	추정 FC 전압	목록

이 모델에 대한 자세한 내용은 여기를 방문하십시오

매개 변수

TestMode : 활성 테스트 모드 및 dict 로 데이터를 얻습니다 (기본값 : False )
ReportMode : 보고서 생성 ( .csv , .opem , .html ) 및 콘솔에서 인쇄 결과 (기본값 : True )
PrintMode : 콘솔에서의 제어 인쇄 (기본값 : True )
Folder : 보고서 폴더, (기본값 : os.getcwd() )

메모

반환 유형 : dict

Telegram Bot

OPEM BOT로 보내기 /start 명령
메뉴에서 모델을 선택하십시오
템플릿에 따라 테스트 벡터를 보내십시오
결과를 다운로드하십시오

브라우저에서 OPEM을 사용해보십시오!

OPEM은 Binder Service를 통해 대화식 Jupyter 노트북에서 온라인으로 사용할 수 있습니다! 지금 시도해보십시오! :

Documents 폴더에서 .ipynb 파일을 확인하십시오
실행 버튼으로 상단 패널에서 단계별로 메모의 각 부분을 편집하고 실행합니다.
전체 시뮬레이션을 실행하려면 Full Run 섹션에서 Test_Vector 편집 할 수 있습니다.

문제 및 버그 보고서

문제를 채우고 설명하십시오. 최대한 빨리 확인하겠습니다! 또는 이메일을 [email protected]로 보내십시오.

Discord 서버에 가입 할 수도 있습니다

출력

HTML
CSV
opem

감사해요

Chart.js
Pyinstaller
draw.io
Zahra Mobasher (로고 디자인)

참조

1- JC Amphlett, RM Baumert, RF Mann, Ba Peppley 및 PR Roberge. 1995. "Ballard Mark IV 고형 중합체 전해질 연료 전지의 성능 모델링." J. 전기 화학. 사회 (The Electrochemical Society, Inc.) 142 (1) : 9-15. doi : 10.1149/1.2043959.

2- Jeferson M. Correa, Felix A. Farret, Vladimir A. Popov, Marcelo G. Simoes. 2005. "양성자 교환 막 연료 전지 시뮬레이션에 사용 된 모델링 파라미터의 민감도 분석." 에너지 변환에 대한 IEEE 거래 (IEEE) 20 (1) : 211-218. doi : 10.1109/tec.2004.842382.

3- Junbom Kim, Seong-Min Lee, Supramaniam Srinivasan, Charles E. Chamberlin. 1995. "경험적 방정식으로 양성자 교환 막 연료 전지 성능의 모델링." 전기 화학 학회지 (전기 화학 학회) 142 (8) : 2670-2674. doi : 10.1149/1.2050072.

4- I. Sadli, P. Thounthong, J.-P. Martin, S. Rael, B. Davat. 2006. "저전압 정적 변환기를 공급하는 PEMFC의 동작." 전원 저널 (Elsevier) 156 : 119–125. doi : 10.1016/j.jpowsour.2005.08.021.

5- J. Padulles, GW Ault, Jr McDonald. 2000. "전력 시스템 시뮬레이션을위한 통합 된 SOFC 플랜트 동적 모델." 전원 저널 (Elsevier) 86 (1-2) : 495-500. doi : 10.1016/s0378-7753 (99) 00430-9.

6- Hauer, K.-H. 2001. "연료 전지 차량 하드웨어 및 소프트웨어를위한 분석 도구 (대체 시스템 설계의 연비 비교 응용 프로그램)." 박사 학위 캘리포니아 대학교 데이비스 대학의 논문, 교통 기술 및 정책.

7- A. Saadi, M. Becherif, A. Aboubou, 내 Ayad. 2013. "양성자 교환 막 연료 전지 정적 모델 비교." 재생 에너지 (Elsevier) 56 : 64-71. doi : dx.doi.org/10.1016/j.renene.2012.10.012.

8- Diego Feroldi, Marta Basualdo. 2012. "PEM 연료 전지 시스템에 대한 설명." 녹색 에너지 및 기술 (Springer) 49-72. doi : 10.1007/978-1-84996-184-4_2

9- Gottesfeld, Shimshon. 중합체 전해질 연료 전지 : 수소 연료 전원에서 재료 문제. http://physics.oregonstate.edu/~hetheriw/energy/topics/doc/electrochemistry/fc/basic/the_polymer_elfollolyte_fuel_cell.htm

10- Mohamed Becherif, Aïcha Saadi, Daniel Hissel, Abdennacer Aboubou, Mohamed Yacine Ayad. 2011. "정적 및 동적 양성자 교환 막 연료 전지 모델." 탄화수소 광산 및 환경 연구 저널 2 (1)

11- Larminie, J., Dicks, A., & McDonald, MS 2003. 연료 전지 시스템 설명 (Vol. 2, pp. 207-225). 영국 Chichester : J. Wiley. doi : 10.1002/9781118706992.

12- Rho, YW, Srinivasan, S., & Kho, Yt 1994. 이론적 분석. ''전기 화학 학회지, 141 (8), 2089-2096. doi : 10.1149/1.2055066.

13- U. Chakraborty, 연료 전지에서 일정한 연료 활용 및 일정한 연료 흐름을위한 새로운 모델, Appl. 공상 과학. 9 (2019) 1066. https://doi.org/10.3390/app9061066.

인용문

연구에서 OPEM을 사용하는 경우이 백서를 인용하십시오.

 @article {haghighi2018,
  doi = {10.21105/joss.00676},
  url = {https://doi.org/10.21105/joss.00676},
  연도 = {2018},
  Month = {Jul},
  게시자 = {The Open Journal},
  볼륨 = {3},
  번호 = {27},
  페이지 = {676},
  저자 = {Sepand Haghighi 및 Kasra Askari와 Sarmin Hamidi와 Mohammad Mahdi Rahimi},
  title = {{opem} : 오픈 소스 {PEM} 셀 시뮬레이션 도구},
  저널 = {오픈 소스 소프트웨어의 저널}
}

opem.bib (bibtex 형식) 다운로드