
La modélisation et la simulation des piles à combustible à membrane d'échange de protons (PEMFC) peuvent fonctionner comme un outil puissant dans la recherche et le développement de sources d'énergie renouvelables. L'outil de simulation PEMFC open source (OPEM) est un outil de modélisation pour évaluer les performances des piles à combustible à membrane d'échange de protons. Ce package est une combinaison de modèles (statique / dynamique) qui prédisent les paramètres de fonctionnement optimaux du PEMFC. L'OPEM contenait des modèles génériques qui accepteront en entrée, non seulement les valeurs des variables de fonctionnement telles que les gaz d'alimentation anode et cathode, la pression et les compositions, la température des cellules et la densité de courant, mais également les paramètres cellulaires, y compris la zone active et l'épaisseur de la membrane. De plus, certains des différents modèles de PEMFC qui ont été proposés dans l'Opem, se concentrent simplement sur une pile FC particulière, et d'autres prennent en compte une partie ou tous les auxiliaires tels que les réformateurs. Opem est une plate-forme de développement collaboratif de modèles PEMFC.
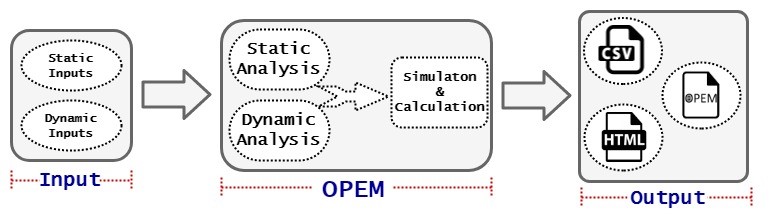
Fig1. Diagramme de blocs Opem
| Hub ouvert | |
| Compteur PYPI | |
| Étoiles github |
| Bifurquer | maître | développer |
| CI |  |  |
| Qualité du code |
Ouvrir CMD (Windows) ou Terminal (UNIX)
Exécuter opem ou python -m opem (ou Run OPEM.exe )
Entrez les paramètres des cellules PEM (ou exécutez des vecteurs de test standard)
Modèle statique Amphlett
| Saisir | Description | Unité |
| T | Température de fonctionnement des cellules | K |
| Ph2 | Pression partielle | ATM |
| PO2 | Pression partielle | ATM |
| Je démêle | Point de départ courant de fonctionnement de la cellule | UN |
| I-Step | Étape de courant de fonctionnement de la cellule | UN |
| i-arrêt | Point final de courant de fonctionnement de la cellule | UN |
| UN | Zone active | cm ^ 2 |
| l | Épaisseur de membrane | cm |
| lambda | Un paramètre réglable avec une valeur min de 14 et une valeur max de 23 | - |
| R (* facultatif) | R-électronique | ohm |
| Jmax | Densité de courant maximale | A / (cm ^ 2) |
| N | Nombre de cellules uniques | - |
Modèle statique de Larminie-Dicks
| Saisir | Description | Unité |
| E0 | Pile à combustible réversible sans tension de perte | V |
| UN | La pente de la ligne Tafel | V |
| T | Température de fonctionnement des cellules | K |
| Je démêle | Point de départ courant de fonctionnement de la cellule | UN |
| I-Step | Étape de courant de fonctionnement de la cellule | UN |
| i-arrêt | Point final de courant de fonctionnement de la cellule | UN |
| dans | Courant interne | UN |
| i_0 | Échange de courant auquel la surtension commence à se déplacer de zéro | UN |
| i_l | Limiter le courant | UN |
| RM | La membrane et les résistances de contact | ohm |
| N | Nombre de cellules uniques | - |
Modèle statique de chambre-kim
| Saisir | Description | Unité |
| E0 | Tension de circuit ouvert | V |
| b | Le paramètre de Tafel pour la réduction de l'oxygène | V |
| R | Résistance | ohm.cm ^ 2 |
| Je démêle | Point de départ courant de fonctionnement de la cellule | UN |
| I-Step | Étape de courant de fonctionnement de la cellule | UN |
| i-arrêt | Point final de courant de fonctionnement de la cellule | UN |
| UN | Zone active | cm ^ 2 |
| m | Paramètres de la diffusion | V |
| n | Paramètres de la diffusion | (A ^ -1) (cm ^ 2) |
| N | Nombre de cellules uniques | - |
Padules Dynamic Model I
| Saisir | Description | Unité |
| E0 | Pas de tension de chargement | V |
| T | Température de la pile à combustible | K |
| Kh2 | Constante de soupape d'hydrogène | kmol.s ^ (- 1) .atm ^ (- 1) |
| Ko2 | Constante de soupape d'oxygène | kmol.s ^ (- 1) .atm ^ (- 1) |
| TH2 | Constante du temps d'hydrogène | s |
| to2 | Constante du temps d'oxygène | s |
| B | Tension d'activation constante | V |
| C | Paramètre constant d'activation | A ^ (- 1) |
| Rincer | Résistance interne à pile à combustible | ohm |
| rho | Rapport d'écoulement d'hydrogène-oxygène | - |
| QH2 | Flux molaire d'hydrogène | kmol / s |
| N0 | Nombre de cellules | - |
| Je démêle | Point de départ courant de fonctionnement de la cellule | UN |
| I-Step | Étape de courant de fonctionnement de la cellule | UN |
| i-arrêt | Point final de courant de fonctionnement de la cellule | UN |
Padules Dynamic Model II
| Saisir | Description | Unité |
| E0 | Pas de tension de chargement | V |
| T | Température de la pile à combustible | K |
| Kh2 | Constante de soupape d'hydrogène | kmol.s ^ (- 1) .atm ^ (- 1) |
| Kh2o | Constante de soupape | kmol.s ^ (- 1) .atm ^ (- 1) |
| Ko2 | Constante de soupape d'oxygène | kmol.s ^ (- 1) .atm ^ (- 1) |
| TH2 | Constante du temps d'hydrogène | s |
| Th2o | Temps d'eau constante | s |
| to2 | Constante du temps d'oxygène | s |
| B | Tension d'activation constante | V |
| C | Paramètre constant d'activation | A ^ (- 1) |
| Rincer | Résistance interne à pile à combustible | ohm |
| rho | Rapport d'écoulement d'hydrogène-oxygène | - |
| QH2 | Flux molaire d'hydrogène | kmol / s |
| N0 | Nombre de cellules | - |
| Je démêle | Point de départ courant de fonctionnement de la cellule | UN |
| I-Step | Étape de courant de fonctionnement de la cellule | UN |
| i-arrêt | Point final de courant de fonctionnement de la cellule | UN |
Modèle dynamique de Padules-Hauer
| Saisir | Description | Unité |
| E0 | Pas de tension de chargement | V |
| T | Température de la pile à combustible | K |
| Kh2 | Constante de soupape d'hydrogène | kmol.s ^ (- 1) .atm ^ (- 1) |
| Kh2o | Constante de soupape | kmol.s ^ (- 1) .atm ^ (- 1) |
| Ko2 | Constante de soupape d'oxygène | kmol.s ^ (- 1) .atm ^ (- 1) |
| TH2 | Constante du temps d'hydrogène | s |
| Th2o | Temps d'eau constante | s |
| to2 | Constante du temps d'oxygène | s |
| T1 | Constante du temps de réformateur | s |
| T2 | Constante du temps de réformateur | s |
| B | Tension d'activation constante | V |
| C | Paramètre constant d'activation | A ^ (- 1) |
| Cv | Facteur de conversion | - |
| Rincer | Résistance interne à pile à combustible | ohm |
| rho | Rapport d'écoulement d'hydrogène-oxygène | - |
| qméthanol | Flux molaire de méthanol | kmol / s |
| N0 | Nombre de cellules | - |
| Je démêle | Point de départ courant de fonctionnement de la cellule | UN |
| I-Step | Étape de courant de fonctionnement de la cellule | UN |
| i-arrêt | Point final de courant de fonctionnement de la cellule | UN |
Modèle dynamique de Padules-Amphlett
| Saisir | Description | Unité |
| E0 | Pas de tension de chargement | V |
| T | Température de la pile à combustible | K |
| Kh2 | Constante de soupape d'hydrogène | kmol.s ^ (- 1) .atm ^ (- 1) |
| Kh2o | Constante de soupape | kmol.s ^ (- 1) .atm ^ (- 1) |
| Ko2 | Constante de soupape d'oxygène | kmol.s ^ (- 1) .atm ^ (- 1) |
| TH2 | Constante du temps d'hydrogène | s |
| Th2o | Temps d'eau constante | s |
| to2 | Constante du temps d'oxygène | s |
| T1 | Constante du temps de réformateur | s |
| T2 | Constante du temps de réformateur | s |
| UN | Zone active | cm ^ 2 |
| l | Épaisseur de membrane | cm |
| lambda | Un paramètre réglable avec une valeur min de 14 et une valeur max de 23 | - |
| R (* facultatif) | R-électronique | ohm |
| Jmax | Densité de courant maximale | A / (cm ^ 2) |
| Cv | Facteur de conversion | - |
| rho | Rapport d'écoulement d'hydrogène-oxygène | - |
| qméthanol | Flux molaire de méthanol | kmol / s |
| N0 | Nombre de cellules | - |
| Je démêle | Point de départ courant de fonctionnement de la cellule | UN |
| I-Step | Étape de courant de fonctionnement de la cellule | UN |
| i-arrêt | Point final de courant de fonctionnement de la cellule | UN |
Modèle dynamique de chakraborty
| Saisir | Description | Unité |
| E0 | Pas de tension de chargement | V |
| T | Température de fonctionnement des cellules | K |
| Kh2 | Constante de soupape d'hydrogène | kmol.s ^ (- 1) .atm ^ (- 1) |
| Kh2o | Constante de soupape | kmol.s ^ (- 1) .atm ^ (- 1) |
| Ko2 | Constante de soupape d'oxygène | kmol.s ^ (- 1) .atm ^ (- 1) |
| rho | Rapport d'écoulement d'hydrogène-oxygène | - |
| Rincer | Résistance interne à pile à combustible | ohm |
| N0 | Nombre de cellules | - |
| u | Ratio d'utilisation du carburant | - |
| Je démêle | Point de départ courant de fonctionnement de la cellule | UN |
| I-Step | Étape de courant de fonctionnement de la cellule | UN |
| i-arrêt | Point final de courant de fonctionnement de la cellule | UN |
Model_Name Enregistrement d'écran
Modèle statique Amphlett
>>> from opem.Static.Amphlett import Static_Analysis
>>> Test_Vector = { " T " : 343.15 , " PH2 " : 1 , " PO2 " : 1 , " i-start " : 0 , " i-stop " : 75 , " i-step " : 0.1 , " A " : 50.6 , " l " : 0.0178 , " lambda " : 23 , " N " : 1 , " R " : 0 , " JMax " : 1.5 , " Name " : " Amphlett_Test " }
>>> data = Static_Analysis( InputMethod = Test_Vector, TestMode = True , PrintMode = False , ReportMode = False )| Clé | Description | Taper |
| Statut | Statut de simulation | Bool |
| P | Pouvoir | Liste |
| je | Courant de fonctionnement cellulaire | Liste |
| V | Tension FC | Liste |
| Effesser | Efficacité | Liste |
| PH | Puissance thermique | Liste |
| V0 | Interception linéaire-APX | Flotter |
| K | Pente linéaire-APX | Flotter |
| Eta_active | Activation ETA | Liste |
| Eta_conc | Concentration d'ETA | Liste |
| Eta_ohmic | Eta ohmic | Liste |
| Ve | Tension FC estimée | Liste |
Modèle statique de Larminie-Dicks
>>> from opem.Static.Larminie_Dicks import Static_Analysis
>>> Test_Vector = { " A " : 0.06 , " E0 " : 1.178 , " T " : 328.15 , " RM " : 0.0018 , " i_0 " : 0.00654 , " i_L " : 100.0 , " i_n " : 0.23 , " N " : 23 , " i-start " : 0.1 , " i-stop " : 98 , " i-step " : 0.1 , " Name " : " Larminiee_Test " }
>>> data = Static_Analysis( InputMethod = Test_Vector, TestMode = True , PrintMode = False , ReportMode = False )| Clé | Description | Taper |
| Statut | Statut de simulation | Bool |
| P | Pouvoir | Liste |
| je | Courant de fonctionnement cellulaire | Liste |
| V | Tension FC | Liste |
| Effesser | Efficacité | Liste |
| PH | Puissance thermique | Liste |
| V0 | Interception linéaire-APX | Flotter |
| K | Pente linéaire-APX | Flotter |
| Ve | Tension FC estimée | Liste |
Modèle statique de chambre-kim
>>> from opem.Static.Chamberline_Kim import Static_Analysis
>>> Test_Vector = { " A " : 50.0 , " E0 " : 0.982 , " b " : 0.0689 , " R " : 0.328 , " m " : 0.000125 , " n " : 9.45 , " N " : 1 , " i-start " : 1 , " i-stop " : 42.5 , " i-step " : 0.1 , " Name " : " Chamberline_Test " }
>>> data = Static_Analysis( InputMethod = Test_Vector, TestMode = True , PrintMode = False , ReportMode = False )| Clé | Description | Taper |
| Statut | Statut de simulation | Bool |
| P | Pouvoir | Liste |
| je | Courant de fonctionnement cellulaire | Liste |
| V | Tension FC | Liste |
| Effesser | Efficacité | Liste |
| PH | Puissance thermique | Liste |
| V0 | Interception linéaire-APX | Flotter |
| K | Pente linéaire-APX | Flotter |
| Ve | Tension FC estimée | Liste |
Padules Dynamic Model I
>>> from opem.Dynamic.Padulles1 import Dynamic_Analysis
>>> Test_Vector = { " T " : 343 , " E0 " : 0.6 , " N0 " : 88 , " KO2 " : 0.0000211 , " KH2 " : 0.0000422 , " tH2 " : 3.37 , " tO2 " : 6.74 , " B " : 0.04777 , " C " : 0.0136 , " Rint " : 0.00303 , " rho " : 1.168 , " qH2 " : 0.0004 , " i-start " : 0 , " i-stop " : 100 , " i-step " : 0.1 , " Name " : " PadullesI_Test " }
>>> data = Dynamic_Analysis( InputMethod = Test_Vector, TestMode = True , PrintMode = False , ReportMode = False )| Clé | Description | Taper |
| Statut | Statut de simulation | Bool |
| P | Pouvoir | Liste |
| je | Courant de fonctionnement cellulaire | Liste |
| V | Tension FC | Liste |
| Effesser | Efficacité | Liste |
| PO2 | Pression partielle | Liste |
| Ph2 | Pression partielle | Liste |
| PH | Puissance thermique | Liste |
| V0 | Interception linéaire-APX | Flotter |
| K | Pente linéaire-APX | Flotter |
| Ve | Tension FC estimée | Liste |
Padules Dynamic Model II
>>> from opem.Dynamic.Padulles2 import Dynamic_Analysis
>>> Test_Vector = { " T " : 343 , " E0 " : 0.6 , " N0 " : 5 , " KO2 " : 0.0000211 , " KH2 " : 0.0000422 , " KH2O " : 0.000007716 , " tH2 " : 3.37 , " tO2 " : 6.74 , " tH2O " : 18.418 , " B " : 0.04777 , " C " : 0.0136 , " Rint " : 0.00303 , " rho " : 1.168 , " qH2 " : 0.0004 , " i-start " : 0.1 , " i-stop " : 100 , " i-step " : 0.1 , " Name " : " Padulles2_Test " }
>>> data = Dynamic_Analysis( InputMethod = Test_Vector, TestMode = True , PrintMode = False , ReportMode = False )| Clé | Description | Taper |
| Statut | Statut de simulation | Bool |
| P | Pouvoir | Liste |
| je | Courant de fonctionnement cellulaire | Liste |
| V | Tension FC | Liste |
| Effesser | Efficacité | Liste |
| PO2 | Pression partielle | Liste |
| Ph2 | Pression partielle | Liste |
| Ph2o | Pression partielle | Liste |
| PH | Puissance thermique | Liste |
| V0 | Interception linéaire-APX | Flotter |
| K | Pente linéaire-APX | Flotter |
| Ve | Tension FC estimée | Liste |
Modèle dynamique de Padules-Hauer
>>> from opem.Dynamic.Padulles_Hauer import Dynamic_Analysis
>>> Test_Vector = { " T " : 343 , " E0 " : 0.6 , " N0 " : 5 , " KO2 " : 0.0000211 , " KH2 " : 0.0000422 , " KH2O " : 0.000007716 , " tH2 " : 3.37 , " tO2 " : 6.74 , " t1 " : 2 , " t2 " : 2 , " tH2O " : 18.418 , " B " : 0.04777 , " C " : 0.0136 , " Rint " : 0.00303 , " rho " : 1.168 , " qMethanol " : 0.0002 , " CV " : 2 , " i-start " : 0.1 , " i-stop " : 100 , " i-step " : 0.1 , " Name " : " Padulles_Hauer_Test " }
>>> data = Dynamic_Analysis( InputMethod = Test_Vector, TestMode = True , PrintMode = False , ReportMode = False )| Clé | Description | Taper |
| Statut | Statut de simulation | Bool |
| P | Pouvoir | Liste |
| je | Courant de fonctionnement cellulaire | Liste |
| V | Tension FC | Liste |
| Effesser | Efficacité | Liste |
| PO2 | Pression partielle | Liste |
| Ph2 | Pression partielle | Liste |
| Ph2o | Pression partielle | Liste |
| PH | Puissance thermique | Liste |
| V0 | Interception linéaire-APX | Flotter |
| K | Pente linéaire-APX | Flotter |
| Ve | Tension FC estimée | Liste |
Modèle dynamique de Padules-Amphlett
>>> from opem.Dynamic.Padulles_Amphlett import Dynamic_Analysis
>>> Test_Vector = { " A " : 50.6 , " l " : 0.0178 , " lambda " : 23 , " JMax " : 1.5 , " T " : 343 , " N0 " : 5 , " KO2 " : 0.0000211 , " KH2 " : 0.0000422 , " KH2O " : 0.000007716 , " tH2 " : 3.37 , " tO2 " : 6.74 , " t1 " : 2 , " t2 " : 2 , " tH2O " : 18.418 , " rho " : 1.168 , " qMethanol " : 0.0002 , " CV " : 2 , " i-start " : 0.1 , " i-stop " : 75 , " i-step " : 0.1 , " Name " : " Padulles_Amphlett_Test " }
>>> data = Dynamic_Analysis( InputMethod = Test_Vector, TestMode = True , PrintMode = False , ReportMode = False )| Clé | Description | Taper |
| Statut | Statut de simulation | Bool |
| P | Pouvoir | Liste |
| je | Courant de fonctionnement cellulaire | Liste |
| V | Tension FC | Liste |
| Effesser | Efficacité | Liste |
| PO2 | Pression partielle | Liste |
| Ph2 | Pression partielle | Liste |
| Ph2o | Pression partielle | Liste |
| PH | Puissance thermique | Liste |
| V0 | Interception linéaire-APX | Flotter |
| K | Pente linéaire-APX | Flotter |
| Eta_active | Activation ETA | Liste |
| Eta_conc | Concentration d'ETA | Liste |
| Eta_ohmic | Eta ohmic | Liste |
| Ve | Tension FC estimée | Liste |
Modèle dynamique de chakraborty
>>> from opem.Dynamic.Chakraborty import Dynamic_Analysis
>>> Test_Vector = { " T " : 1273 , " E0 " : 0.6 , " u " : 0.8 , " N0 " : 1 , " R " : 3.28125 * 10 ** ( - 3 ), " KH2O " : 0.000281 , " KH2 " : 0.000843 , " KO2 " : 0.00252 , " rho " : 1.145 , " i-start " : 0.1 , " i-stop " : 300 , " i-step " : 0.1 , " Name " : " Chakraborty_Test " }
>>> data = Dynamic_Analysis( InputMethod = Test_Vector, TestMode = True , PrintMode = False , ReportMode = False )| Clé | Description | Taper |
| Statut | Statut de simulation | Bool |
| P | Pouvoir | Liste |
| je | Courant de fonctionnement cellulaire | Liste |
| V | Tension FC | Liste |
| Effesser | Efficacité | Liste |
| PO2 | Pression partielle | Liste |
| Ph2 | Pression partielle | Liste |
| Ph2o | Pression partielle | Liste |
| PH | Puissance thermique | Liste |
| Gain de Nernst | Gain de Nernst | Liste |
| Perte ohmique | Perte ohmique | Liste |
| V0 | Interception linéaire-APX | Flotter |
| K | Pente linéaire-APX | Flotter |
| Ve | Tension FC estimée | Liste |
TestMode : Mode de test actif et données Get / Return comme dict , (par défaut: False )ReportMode : générer des rapports ( .csv , .opem , .html ) et un résultat imprimé dans la console, (par défaut: True )PrintMode : Control Printing in Console, (par défaut: True )Folder : Rapports Folder, (par défaut: os.getcwd() ) dict/start à Opem BotL'OPEM peut être utilisé en ligne dans des cahiers de jupyter interactifs via le service de liant! Essayez-le maintenant! :
.ipynb dans le dossier DocumentsTest_Vector dans la section Full Run Remplissez simplement un problème et décrivez-le. Nous allons le vérifier dès que possible! Ou envoyez un e-mail à [email protected].
Vous pouvez également rejoindre notre serveur Discord
1- JC Amphlett, RM Baumert, RF Mann, Ba Peppley et PR Roberge. 1995. "Modélisation des performances de la pile d'électrolyte en polymère solide de Mark IV Ballard." J. Electrochem. Soc. (The Electrochemical Society, Inc.) 142 (1): 9-15. doi: 10.1149 / 1.2043959.
2- Jeferson M. Correa, Felix A. Farret, Vladimir A. Popov, Marcelo G. Simoes. 2005. "Analyse de sensibilité des paramètres de modélisation utilisés dans la simulation des piles à combustible à membrane d'échange de protons". Transactions IEEE sur la conversion d'énergie (IEEE) 20 (1): 211-218. doi: 10.1109 / TEC.2004.842382.
3- Junbom Kim, Seong-Min Lee, Supramaniam Srinivasan, Charles E. Chamberlin. 1995. «Modélisation des performances des piles à combustible à membrane d'échange de protons avec une équation empirique». Journal of the Electrochemical Society (The Electrochemical Society) 142 (8): 2670-2674. doi: 10.1149 / 1.2050072.
4- I. Sadli, P. Thounthong, J.-P. Martin, S. Rael, B. Davat. 2006. "Comportement d'un PEMFC fournissant un convertisseur statique à basse tension." Journal of Power Sources (Elsevier) 156: 119–125. doi: 10.1016 / j.jpowsour.2005.08.021.
5- J. Padules, GW Ault, Jr McDonald. 2000. "Un modèle dynamique de plante SOFC intégré pour la simulation des systèmes d'alimentation." Journal of Power Sources (Elsevier) 86 (1-2): 495-500. doi: 10.1016 / s0378-7753 (99) 00430-9.
6- Hauer, K.-H. 2001. "Outil d'analyse pour le matériel et les logiciels du véhicule à pile à combustible (commandes) avec une application sur les comparaisons de l'économie de carburant des conceptions de systèmes alternatifs." doctorat Dissertation, technologie de transport et politique, Université de Californie Davis.
7- A. Saadi, M. Beherif, A. Aboubou, My Ayad. 2013. "Comparaison des modèles statiques de piles à combustible d'échange de protons." Énergie renouvelable (Elsevier) 56: 64-71. doi: dx.doi.org/10.1016/j.rennene.2012.10.012.
8- Diego Feroldi, Marta Basualdo. 2012. «Description du système de piles à combustible PEM». Énergie et technologie vertes (Springer) 49-72. doi: 10.1007 / 978-1-84996-184-4_2
9- Gottesfeld, Shimshon. et la pile à combustible électrolyte en polymère: problèmes de matériaux dans une source d'alimentation alimentée par l'hydrogène. http://physics.oregonstate.edu/~hetheriw/energy/topics/doc/electrochimie/fc/basic/the_polymer_electrolyte_fuel_cell.htm
10- Mohamed Beherif, Aïcha Saadi, Daniel Hissel, Abdennacer Aboubou, Mohamed Yacine Ayad. 2011. «Modèles de pile à combustible à membrane d'échange de protons statiques et dynamiques. Journal of Hydrocarbons Mines and Environmental Research 2 (1)
11- Larminie, J., Dicks, A., et McDonald, MS 2003. Systèmes de piles à combustible expliquées (Vol. 2, pp. 207-225). Chichester, Royaume-Uni: J. Wiley. doi: 10.1002 / 9781118706992.
12- Rho, YW, Srinivasan, S., et Kho, Yt 1994. '' Phénomènes de transport de masse dans les piles à combustible à membrane d'échange de protons en utilisant O 2 / He, O 2 / Ar et O 2 / N 2 mélanges II. Analyse théorique. '' Journal of the Electrochemical Society, 141 (8), 2089-2096. doi: 10.1149 / 1.2055066.
13- U. Chakraborty, Un nouveau modèle pour l'utilisation constante du carburant et le débit de carburant constant dans les piles à combustible, Appl. Sci. 9 (2019) 1066. Https://doi.org/10.3390/app9061066.
Si vous utilisez OPEM dans vos recherches, veuillez citer cet article:
@article {haghighi2018,
doi = {10.21105 / joss.00676},
url = {https://doi.org/10.21105/joss.00676},
année = {2018},
mois = {juil},
éditeur = {The Open Journal},
volume = {3},
nombre = {27},
pages = {676},
Auteur = {Sepand Haghighi et Kasra Askari et Sarmin Hamidi et Mohammad Mahdi Rahimi},
title = {{opem}: open source {pem} outil de simulation de cellules},
journal = {Journal of Open Source Software}
}
Télécharger opem.bib (format Bibtex)
| Joss | |
| Zenodo |
Donnez un ️ si ce projet vous a aidé!
Si vous aimez notre projet et que nous espérons que vous le faites, pouvez-vous nous soutenir? Notre projet n'est pas et ne fonctionnera jamais à but lucratif. Nous avons besoin de l'argent juste pour continuer à faire ce que nous faisons ;-).