Dans l'eau, la direction le long du ruisseau est appelée en aval. Et, la direction contre le ruisseau est appelée en amont.
Si la vitesse d'un bateau dans l'eau immobile est u km / h et que la vitesse du ruisseau est en v km / h, alors:
Vitesse en aval = (u + v) km / h.
Accélérer en amont = (u - v) km / h.
Si la vitesse en aval est un kilomètre / h et que la vitesse en amont est B km / h, alors:
Vitesse dans l'eau immobile = 1/2 * (A + B) km / h.
Taux de flux = 1/2 * (a - b) km / h.
Bénéfice, p = sp - cp; Sp> cp
Perte, L = CP - SP; Cp> sp
P% = (p / cp) x 100
L% = (l / cp) x 100
Sp = {(100 + p%) / 100} x cp
Sp = {(100 - l%) / 100} x cp
Cp = {100 / (100 + p%)} x sp
Cp = {100 / (100 - l%)} x sp
Remise = MP - SP
Sp = MP -Discou
Pour le faux poids , le pourcentage de profit sera P% = (Poids vrai - faux poids / faux poids) x 100 .
Lorsqu'il y a deux bénéfices réussis, disent M% et N%, le pourcentage net net est équivalent à (m + n + mn) / 100
Lorsque le bénéfice est M% et que la perte est N%, le bénéfice ou la perte net en% sera: (Mn-Mn) / 100
Si un produit est vendu à M% de profit, puis vendu à N% de profit , le prix de coût réel du produit sera: CP = [100 x 100 x p / (100 + m) (100 + n)] . En cas de perte , CP = [100 x 100 x p / (100 m) (100-n)]
Si p% et l% sont égaux alors, p = l et % pertes = p ^ 2/100

Pour vérifier multiplier le nombre par 5 ou 2 et que ce nombre, ajoutez (si Mul par 5) sinon si Mul par 2 (soustrait) par numéro gauche
par exemple: 532 div par 7
Étape 1- MUL 2X5 = 10 Étape 2- négligez le chiffre d'unité et ajoutez au numéro de gauche 53 | 2 + 10 = 63
Vérifiez le numéro divisible si oui que le numéro d'origine est également divisible.
SIMILARY Multipliez-le par 2 et ajoutez plutôt soustrayez-le.
Multipliez le chiffre d'unité par 5 et soulignez qui multiplié par la valeur avec le chiffre de repos si ce multile que le nombre est divisible par 17.
par exemple: 272 iv par 17
Étape 1-
Mul 2 * 5 = 10 ** Étape 2- **
27-10 = 17 17 est divisible par 17, donc 272 est divisible par 17.


Le visage ou le cadran de l'horloge est un cercle dont la circonférence est divisée en 60 parties égales, nommées de minuscules espaces.
Main et main-midi à main, une horloge a deux mains. La plus petite main est appelée main ou main courte et la plus grande est appelée main-midi ou main longue.
En 60 minutes, les minutes à main gagnent 55 minutes sur les espaces sur la main de l'heure.
(En 60 minutes, Hour Hand déplacera des espaces de 5 minutes tandis que la main des minutes déplacera des espaces de 60 minutes. En fait, le gain d'espace de la main minute par rapport à la main de l'heure sera de 60 à 5 = 55 minutes.)
Les deux mains d'une horloge coïncident une fois sur l'heure.
Les mains d'une horloge sont dans la même ligne droite lorsqu'elles sont coïncidentes ou opposées les unes aux autres.
Lorsque les deux mains d'une horloge sont à angle droit , ils sont séparés de 15 minutes .
Lorsque les mains d'une horloge sont dans des directions opposées, ce sont des espaces à 30 minutes.
Angle tracé par une main à 12 heures = 360 °
Angle tracé par une main de minute en 60 min. = 360 ° .
Thêta (aka degré) = 30 x h- (11/2) xm
Angle de réflax = 360 - thêta
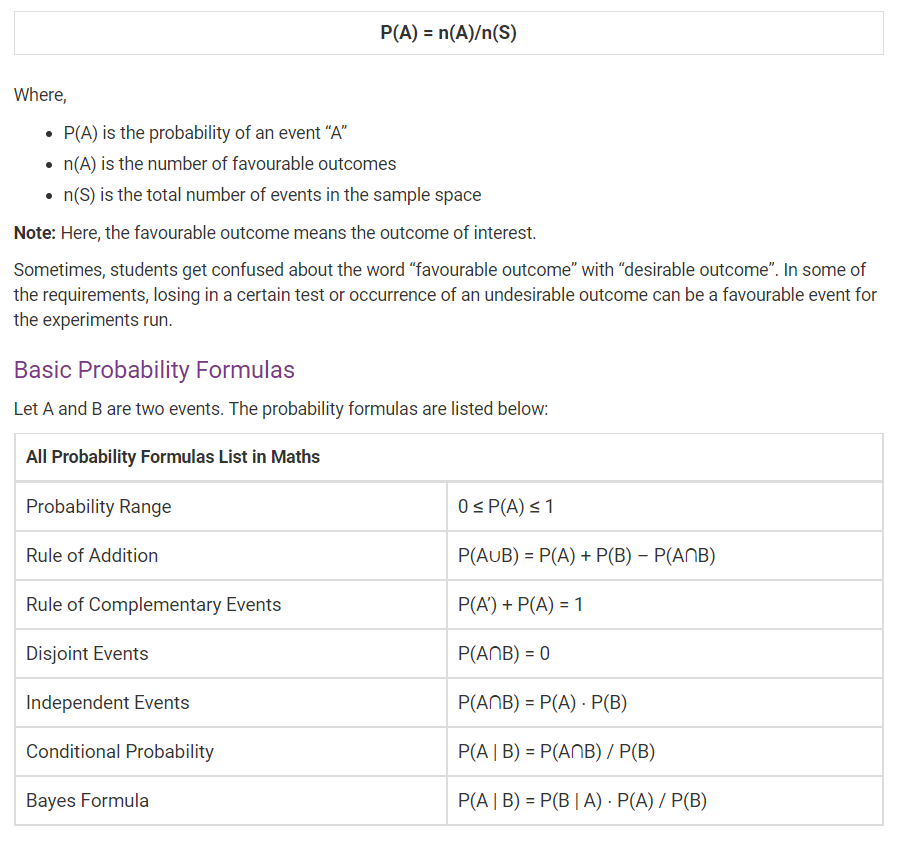


1. Nombres naturels (n) = 1, 2, 3 ,. . . . 2. Nombres entiers (W) = 0, 1, 2, 3 ,. . . . 3. Intezers (z) = −∞. . . −2, −1, 0, 1, 2, 3 ,. . . 4. Nombres rationnels (Q) = les nombres de la forme P⁄Q où q ≠ 0. EG: 1⁄5, 0,46, 0,333333, ils se terminent, répétant . 5. Nombres irrationnels (i) = les nombres de la forme x1⁄n ≠ intezer. Également π et e nombres irrationnels, ils ne sont pas terminants, non répétés .
Autres types de nombres: a. Même nombres: nombres qui sont exactement divisibles par 2. Ces nombres sont dans le format de 2n. né Nombres impairs: nombres qui donnent le reste 1 lorsqu'il est divisé par 2. Ces nombres sont dans le format de 2n ± 1. C. Nombres premiers: les nombres qui sont divisibles par 1 et le nombre lui-même sont des nombres premiers. Le moins Prime est 2. D. Nombres composites: dont les nombres sont divisibles par plus de 2 nombres.
Odd ± Odd = même;
même ± même = même;
Même ± étrange = bizarre
Odd × Odd = Odd;
même × même = même;
Même × Odd = même.
Odd (n'importe quel nombre) = Odd
même (n'importe quel nombre) = même
(a - b) 2 = (a2 + b2 - 2ab)
(A + B) 2 = (A2 + B2 + 2AB)
(a + b) (a - b) = (a2 - b2)
(A3 + B3) = (A + B) (A2 - AB + B2)
(A3 - B3) = (A - B) (A2 - AB + B2)
(A + B + C) 2 = A2 + B2 + C2 + 2 (AB + BC + CA)
(A3 + B3 + C3 - 3ABC) = (A + B + C) (AR> 2 + B2 + C2 - AB - BC - AC)
Conseils et astuces rapides
Étape 1: Lors de la simplification des expressions données, les premiers supports doivent être supprimés dans l'ordre: '––', '()', '{}', '[]'
Étape2: Les opérations doivent être effectuées strictement dans l'ordre: division, multiplication, addition et soustraction
Bodmas est le raccourci utilisé pour se souvenir de la procédure de simplification.
B: support
O: commande (c.-à-d. Root carré, etc.)
D: Division (de gauche à droite)
M: Multiplication (de gauche à droite)
R: Ajout (de gauche à droite)
S: soustraction (de gauche à droite)
Étape 1: Lors de la simplification des expressions données, les premiers supports doivent être supprimés dans l'ordre: (), {}, []
Étape2: Les opérations doivent être effectuées strictement dans l'ordre: division, multiplication, addition et soustraction
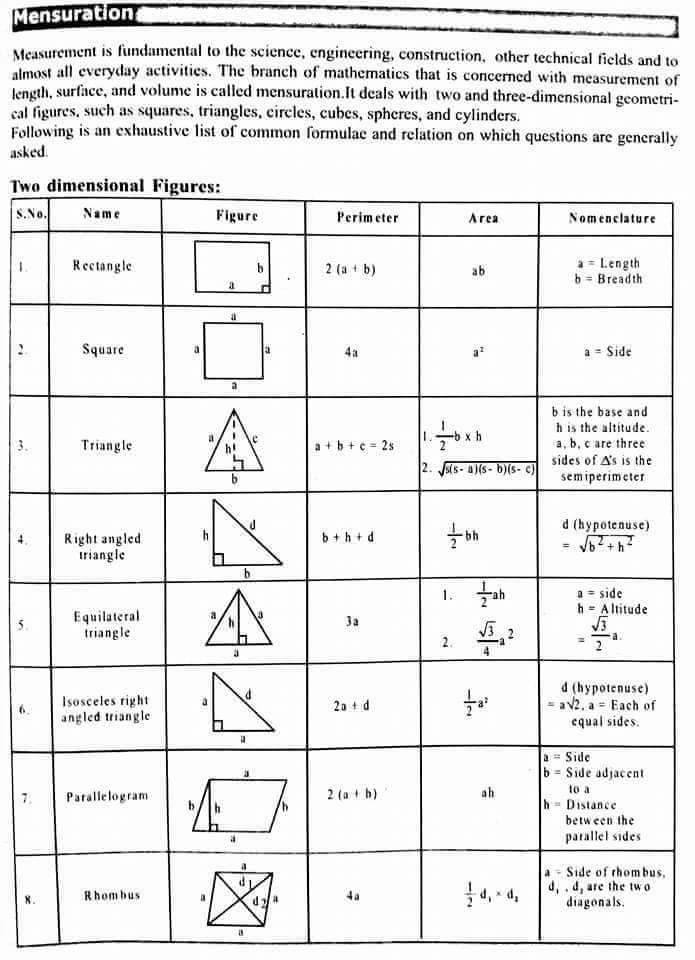
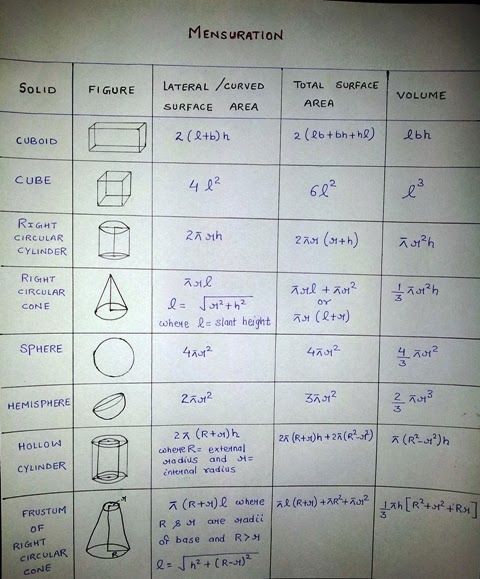
** Formule importante: **
Formule importante
Somme de carré de n nombre naturel = n (n + 1) (2n + 1) / 2
Somme de n nombre naturel = n (n + 1) / 2
Somme dans ap = nx (a + l) / 2
Avg du premier n nombre impair = n
Avg du premier n nombre uniforme = n + 1
Avg de n naturat numéro = (n + 1) / 2
Avg de nombre * nombre total = somme
Question basée sur la population
Rapport et proportion
Code / décodage
Enregistrer
Question verbale amcat
Reste négatif
Test d'admissibilité
735/2
735/704
3/704
3/735
Solution
Option A
Find the LCM of the numerators.
LCM (147, 30) = 1470
Step 2: Find the HCF of denominators.
HCF (64, 44) = 4
So, the LCM of 147/64 and 30/44 is (LCM of Numerators) / (HCF of Denominators) = 1470 / 4 = 735/2
A) 5 mph
B) 10 mph
C) 12 mph
D) 20 mph
Solution
Option C
Let the speed of the river=x mph, then
Time taken row 30 miles upstream and 30 miles downstream = 30/(15-x) + 30/(15+x) = 9/2
= 10/(15-x) + 10/(15+x) = 3/2
= 2[10(15+x) + 10(15-x)] = 3(15-x)²
= 300 + 20x + 300 – 20x = 675 -3x²
x² = 25 or x=5
A) 3 jours
B) 4 jours
C) 4,5 jours
D) 5,4 jours
Solution
option A
Working 5 hours a day, A can complete the work in 8 days = 5*8 = 40 hours
Working 6 hours a day, B can complete the work in 10 days = 6*10 = 60 hours
(A+B)’s 1 hour’s work = (1/40+1/60)
=(3+2)/120
= 1/24
Hence, A and B can complete the work in 24 hours which is equal to 3 days.
A) 6,5 litres
B) 5 litres
C) 4 litres
D) 7,5 litres
Solution
Option B
A mixture of 40 liters of milk = 36 liters of Milk and 4 liters of water = 90:10 ratio
Now the new mixture should be in the ratio of 80:20
Hence 80% is equivalent to 36 liters (no addition of milk is done)
100% is (36/80)*100 = 45 liters of milk is present in the new mixture
Thus water shall be added= (45 – 36 – 4) = 5 liters of water
**or**

A) 12 minuit
B) 3h du matin
C) 6h du matin
D) 9h
Solution
Option D
Four different devices beep after every 30 mins, 60 mins, 90 mins and 105 mins.
LCM of 30,60,90 and 105 is 1260.
Which means the devices beep together after every 1260 mins = 1260/60 = 21 hours
Hence 12 noon + 21 hours = 9 a.m
A) 21 m
B) 26 m
C) 28 m
D) 29 m
Solution
Option C
When A travels 100 m, B travels 75 m. Hence A:B = 100:75
When B travels 100 m, C travels 96 m. Hence B:C = 100:96
When B Travels 75 m, C travels (96 x 75)/100 = 72 m
Hence B:C = 75:72.
Therefore, A:B:C = 100:75:72.
So, when A Travels 100 m, C travels 72 m.
Therefore, A beat C by 28 m
A) 62
B) 68
C) 66
D) 69
Solution
Option A
70% students passed in physics = 30% failed in Physics.
65% students passed in Chemistry = 35% failed in Chemistry
Percentage of students failed in both subject = 27%.
Percentage of students failed = 35 + 30 – 27
= 38%.
Percentage of students passed = 100 – 38% = 62%
A) 40
B) 60
C) 100
D) 160
Solution
Option D
15 oxen take 80 days so, 6 oxen take x days
x = 15*80/6 = 200 days
20 oxen also take 80 day. So, 2 cows take y days
y = 20*80/2 = 800 days
Together work will be done in 800*200/(800+200) = 160 days
A) 297/10377
B) 188/121
C) 21/34
D) 33/163
Solution
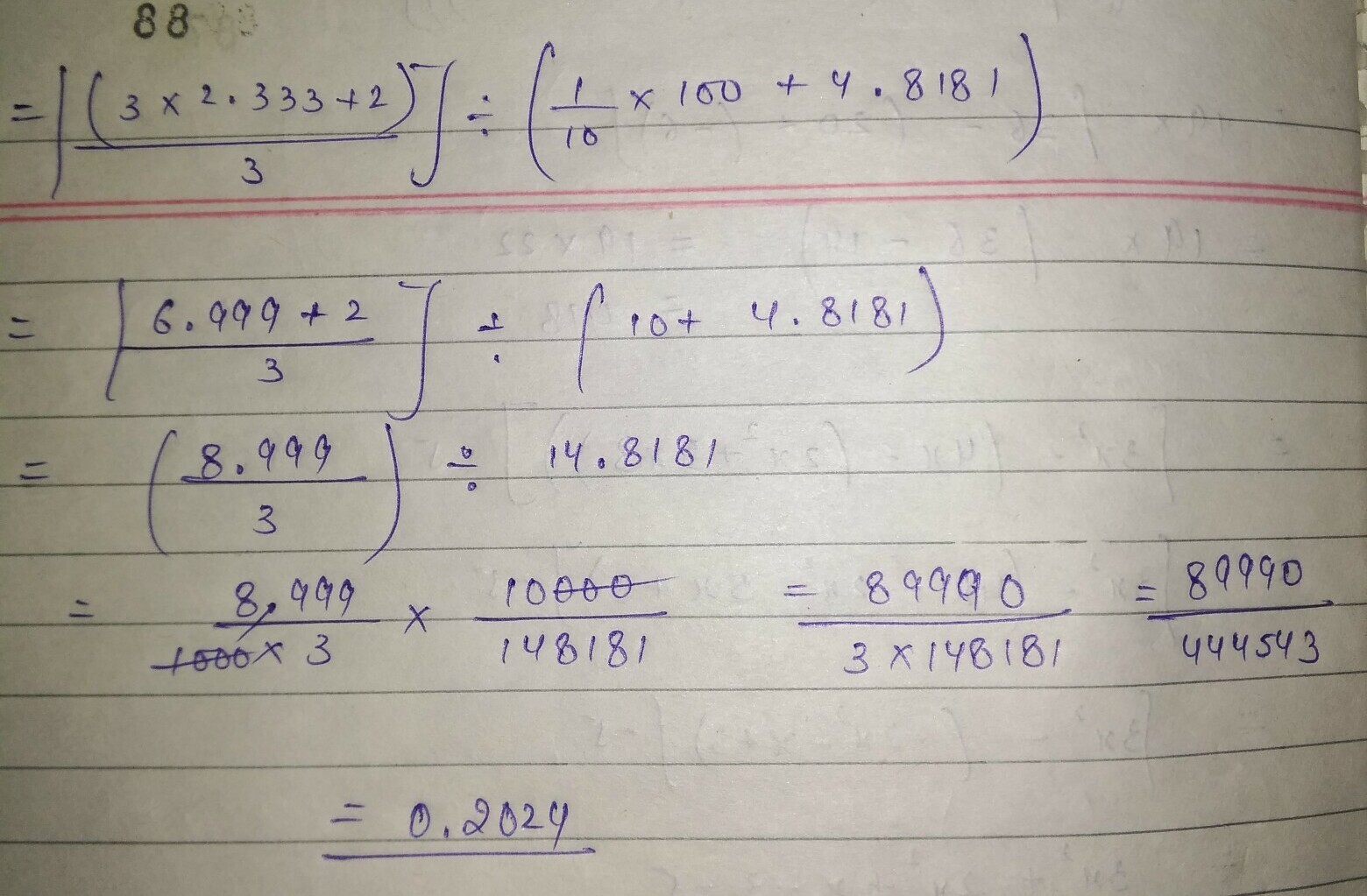
Solution: Option D
A) 6c4
B) 6p4
C) 4 ^ 6
D) 6 ^ 4
Solution
C is correct because all 4 can get 4 ticket one by one
A) 550
B) 450
C) 350
D) 150
Solution
Option B
Going through the options,
Taking Cost Price as Rs 450.
Profit = 650 – 450 = 200
Loss = 350 – 450 = 100
Clearly profit is twice the loss incurred.
Hence, Rs 450 is the correct option.
A) 7 heures 30 minutes
B) 8 heures
C) 8 heures 15 minutes
D) 8 heures 25 minutes
Solution
Option C
In 1hr, Ronald types = 32/6 pages and Elan types = 40/5 pages
If they work together they will type = 32/6 + 40/5 = 40/3 pages in 1 hr
Time needed to complete the assignment is = (3 x 110)/40 = 33/4 = 8hrs 15mins
Hence, the time required is 8 hrs 15 mins.
A) diminué de 20%
B) a augmenté de 20%
C) a augmenté de 10%
D) diminué de 10%
Solution
Option D
Let the initial Price = Rs.100 and initial sales = 100
So, the initial revenue = Rs. 10000
Now, the price is reduced to 25% which is equal to Rs.75 and Sales is increased by 20% which is equal to 120.
Now new revenue = 120 x 75 = Rs. 9000
Change in revenue = (10000 – 9000) = Rs.1000 decrease
% decrease = (1000/10000) x 100 = 10%
Hence, the correct option is decrease of 10%.
A) 19/21
B) 3/7
C) 2/21
D) 1/3
Solution
Option A
Probability of getting atleast one nestle chocolate = [(10C1 x 5C1) + 10C2] / 15C2
[(10 x 5) + (10 x 9)/2] / [(15 x 14)/2] = 19/21.
Hence, the required probability is 19/21.
A) Rs 7490
B) Rs 7350
C) Rs 8250
D) Rs 8530
E) aucun de ces
Solution
Option B
Solution:
Share of Anil : Share of Ruhi : Share of Teena is
2000×8 + 2600×4 : 2800×8 + 3200×4 : 4200×4
33 : 44 : 21
so share of Teena = 21/(33+44+21) × 34300 = Rs 7350
A) Rs 3200
B) Rs 4500
C) Rs 3800
D) Rs 3500
E) Rs 2800
Solution:
Option C
Solution:
Rs 3800
Solution:
(7000-x)*8*4/100 = x [ (1 + 10/100)2 – 1] + 226
70*8*4 – 32x/100 = 21x/100 + 226
2240 – 226 = 53x/100
2014 = 53x/100
So, x = Rs 3800
A) 16
B) 18
C) 12
D) 10
E) 22
Solution:
Option A
Solution:
20 men in 8 days so 16 men in 20 × 8/16 = 10 days and
25 women in 12 days so 10 women in 25 × 12/10 = 30 days
So in 3 days, they complete (1/10 + 1/30) × 3 = 2/5
So remaining work = 1 – 2/5 = 3/5
20 m 1 work in 8 days and x men 3/5 work in 6 days
So 20 × 8 × 3/5 = x × 6 × 1
So, x = 16 men
A) 3/5
B) 2/9
C) 1/8
D) 3/7
E) aucun de ces
Solution:
Option D
Solution
Number of multiples of 3 in 140 = 140/3 = 46
Number of multiples of 7 in 140 = 140/7 = 20
Number of multiples of 3×7= 21 in 140 = 140/21 = 6
So required probability = (46+20 – 6)/140 = 60/140 = 3/7
A. Mère
B. sœur
C. nièce
D. tante maternelle
Solution C
A) A
B) b
C) c
D) e
Solution:
E
Solution:
D is father of A and grandfather of F. So, A is father of F.
Thus. D and A are the two fathers. C is the sister of F So. C is the daughter of A.
Since there is only one mother, it is evident that E is the wife of A and hence the mother of C and F.
So, B is brother of A There are three brothers. So. F is the brother of C.
Clearly, A is E's Husband.
A) Mère
B) sœur
C) tante
D) grand-mère
Solution:
C
Solution:
Only son of Amar's mother's father — Amar's maternal uncle.
So, the girl's maternal uncle is Arnar's maternal uncle. Thus, the girl's mother is Amar's aunt.
A) 12
B) 13
C) 14
D) 15
Solution:
A
Solution:
A+B=B+C+12
so
A=12
Solution:
P=(3*2*5)/1=30
Q=(4*2*5)/1=40
Solution:
(150+x)/15=16.
=)150+x=240
=x=90
Moyenne de leur âge = somme / nombre =) 90/5 = 18
A. 154 °
B. 170 °
C. 160 °
D. 180 °
Solution:
We know that angle traced by hour hand in 12 hrs = 360°
From 8 to 2, there are 6 hours.
Angle traced by the hour hand in 6 hours = 6×360/12= 180°
A. 120 °
B. 125 °
C. 130 °
D. 135 °
Solution:
C
Solution:
Angle traced by hour hand in 12 hrs. = 360°.
Angle traced by it in 11/3 hrs = (360/12 x 11/3)° = 110°.
Angle traced by minute hand in 60 min. = 360°.
Angle traced by it in 40 min. = (360/60x40)°= 240°.
Required angle (240 - 110)° = 130°.
A. 3.6
B. 7.2
C. 8.4
D. 10
Solution:
B
Solution:
Speed =600/(5 x 60)= 2 m/sec.
Converting m/sec to km/hr (see important formulas section)
= (2 x18/5)km/hr= 7.2 km/hr.
A. 10
B. 8
C. 6
D. 4
Solution:
C
Opposite direction
speed=60+6=66km/h
time=distance/speed=110/66=5/3 km/h
in m/s 5/3x18/5=6
A. 14,4 secondes
B. 15,5 secondes
C. 18,8 secondes
D. 20,2 secondes
Solution :
A
Solution :
Let length of each train be x meter.
Then, speed of 1st train = x/18m/sec
Speed of 2nd train = x/12 m/sec
Now,
When both trains cross each other, time taken
=2x/(x/18+x/12)=2x/(2x+3x)/36=(2x X 36)/5x=725=14.4seconds
767 495 359 291 257?
A. 230 B. 240 C. 250 D. 280 E. 260
Soluton:
B
Solution:
797-495=272
495-359=136
So which means it is half of previous diffrences
272/2=136
291-257=32
34/2=17
So subtract 17
257-17=240
50 67 33 84 16?
A. 101 B. 109 C. 107 D. 103 E. 201
Solution:
A
Solution:
17 is the gap once increase and than decrease follow this order you will get the answer
192
10
38
2
3
Solution:
3
Solution:
Logic is 2×1 + 1 = 3, 3 × 2 + 4 =10, 10 × 3 + 9 = 39, 39 × 4 + 16 = 172…. So in place of 38, it should be 39.
999980
999990
999984
Rien de ces
Solution:
Greatest six-digit number is 999999. Divide this number by 12 and get remainder as 3. Since the remainder is 3, if you subtract 3 from the number, the remaining number will be a multiple of 12. So the greatest such number will be 999999 – 3 =999996.
5000
4950
4980
4900
Rien de ces
Solution:
Multiples of 3 between 100 and 200 are 102, 105, 108,… ,198.
Here, the first term = 102
last term = 198
Let the number of Multiples of 3 between 100 and 200 = n
W.K.T: Arithmetic Progression Formula:
an = a1 + (n - 1)d
Where, an = last term = 198
a1 = first term = 102
d = common difference = 105 - 102 = 3
---> 198 = 102 + (n - 1) * 3
---> 198 - 102 = (n - 1) * 3
---> 96 = (n - 1) * 3
---> (n - 1) = 96/3 = 32
---> n = 32 + 1
---> n = 33
Formula:
Sum of n terms = Sn = (n/2) * (a + l)
where n = number of elements = 33
a = first term = 102
l = last term = 198
Thus, using the above formula, Sum of all natural numbers between 100 and 200 which are multiples of 3 = (33/2) * (102 + 198)
= (33/2) * 300
= 33 * 150
= 4950
A. 5, 15, 25
B. 12, 15, 18
C. 10, 15, 20
D. -10, -15, -20
Solution:
Assuming that the numbers are (a – d), a, (a + d) and their sum is 45, we get the middle number as 15. Now, the product (a – d) (a + d) = 200. Solving, we get d = 5. Therefore, the numbers are 10, 15 and 20.
Solution:
x/(y+1)=1/2
and
(x+1)/y=1
2x-y=1 ....eq (1)
x=y-1 ....eq (2)
by solving eq 1 and 2 we get
x=2 and y=3
A. 80
B. 75
C. 42
D. 53
Répondre:
Option D
Solution:
As the Number gives a remainder of 4 when it is divided by 7, then the number must be in form of (7x + 4)
The same gives remainder 1 when it is divided 4, so the number must be in the form of {4 × (7x + 4) + 1}
Also, the number when divided by 3 gives remainder 2, thus number must be in form of [3 × {4 × (7x + 4) + 1} + 2]
Now, On simplifying,
[3 × {4 × (7x + 4) + 1} + 2]
= 84x + 53
We get the final number 53 more than a multiple of 84 Hence, if the number is divided by 84,
The remainder will be 53
A) 55/601
B) 601/55
C) 11/120
D) 120/11
Solution:
Then, a + b = 55 and ab = 5 x 120 = 600.
The required sum =1a+1b = a+bab= 55600=11120
Solution:
5
2, 3, 5, 8, 13, 20, 34
Solution:
first+second=third
follow this order you get **20** as a answer
196, 169, 144, 121, 100, 80
Solution:
80
First - Second=2
A. CMN
B. Uji
C. vij
D. IJT
Solution:
C
Olnnie
Oilen
Noilen
Lnoeni
Onnlie
Solution:
1
un. 9 ans
né 10 ans
c. 13 ans
d. 15 ans
Solution:
Correct Option: (c)
We have to find the population of cities A and B after x years.
Step 1: Population of city A = 68000, decreases at the rate of 1200/year
68000 – 1200x
Step 2: Population of city B = 42000, increases at the rate of 800/year
42000 + 800x
Step 3: Find after how many population of cities A and B are equal.
Population of city A = Population of city B
68000 – 1200x = 42000 + 800x
68000 – 42000 = 1200x + 800x
26000 = 2000x
x = 13
un. 28 jours
né 30 jours
c. 34 jours
d. 40 jours
Solution:
Correct Option: (b)
Step 1: Number of days worked by the worker = 60 and he remained idle for x days. Therefore, number of days worked = (60 – x)
Step 2: Each day he was getting paid Rs. 20. Therefore, the payment received for working days = (60 – x) 20
Step 3: After subtracting the amount which he forfeited, he receives Rs. 300.
Therefore,
(60 – x) 20 – 10x = 300
1200 – 20x – 10x = 300
900 = 30x
x = 30 days
un. 11
né 15
c. 16
d. 18
Solution:
Correct Option: (b)
Let’s the number of farmers be y.
Step 1: Find number of heads
= (50 hens + 45 goats + 8 horses + y farmers)
= (103 + y)
Step 2: Number of feet
= [(Hens 2 × 50) + (45 × 4) + (8 × 4) + (y × 2)]
= [100 + 180 + 32 + 2y]
= 312 + 2y
Step 3: Find number of farmers
(312 + 2y) – (103 + y) = 224
312 + 2y – 103 – y = 224
y = 15
A) 49500
B) 49950
C) 45000
D) 49940
Solution:
The Correct answer is (B)
Answer with explanation:
The digit 5 has two place values in the numeral, 5 * 105 = 50,000 and 5 * 101 = 50.
∴Required difference = 50000 - 50 = 49950
A) Rs. 180
B) Rs. 204
C) Rs. 210
D) Rs. 220
Solution:
Option B
CI=P(1+r/100)^t
CI=2500*(1+4/100)^2
CI=2704
So the diffrenece is 204
A) Rs. 5222.2
B) Rs. 5777.7
C) Rs. 6222.2
D) Rs. 6777.7
Solution:
Option B
80000*12/65000*6=32/13
113/32*20000=5777.7rs
A) Jeudi
B) Mercredi
C) Vendredi
D) Dimanche
Solution:
The correct option is (B)
Explanation:
The year 1996 is divisible by 4, so it is a leap year with 2 odd days.
As per the question, the first day of the year 1996 was Monday, so the first day of the year 1997 must be two days after Monday. So, it was Wednesday.
A) 1,5 km / h
B) 2 km / h
C) 2,5 km / h
D) 1 km / h
Solution:
The correct answer is B
Answer with explanation:
Let the speed of stream = X km/hr
Speed of boat = 5 km/hr
Speed upstream = 3km/hr
Apply formula: Speed upstream = speed of boat - speed of stream
∴ 3 = 5 - X
X = 5 - 3 = 2 km/hr
A) 24
B) 22
C) 23
D) 21
Solution:
The Correct answer is (B)
Explanation:
The hands of a clock coincide only once between 11 O' clock and 1 O' clock, so in every 12 hours, the hands of a clock will coincide for 11 times.
∴ In a day or 24 hours, the hands of a clock will coincide for 22 (11+11) times.
A) 10 heures
B) 12 heures
C) 14 heures
D) 16 heures
Solution:
Option B
Water enter in 1 hr=1/6
Water empty in 1 hr=1/12
net=1/6-1/12=1/12
or 12hr
A) 8,5 km / s
B) 7,5 km / s
C) 9,5 km / s
D) 6,5 km / s
Solution:
Option B
sec=4*60=240s
speed=500/240=25/12m/s
in km/s speed is =25/12*18/5=7.5km/s.
Solution:
Surface area of cube=6a^2
600=6*a^2
a=10
diagonal of cube=sqrt(3)*a
ans=sqrt(3)*10
Le HCF de deux nombres est de 23 et les deux autres facteurs de leur LCM sont de 13 et 14. Le plus grand des deux nombres est:
A. 276
B. 299
C. 322
D. 345
Solution:
Answer: Option C
Explanation:
Clearly, the numbers are (23 x 13) and (23 x 14).
Larger number = (23 x 14) = 322.
Six cloches commencent à pénétrer ensemble et pénètrent à des intervalles de 2, 4, 6, 8 10 et 12 secondes respectivement. En 30 minutes, combien de fois se tiennent-ils ensemble?
A. 4
B. 10
C. 15
D. 16
Solution:
Answer: Option D
Explanation:
L.C.M. of 2, 4, 6, 8, 10, 12 is 120.
So, the bells will toll together after every 120 seconds(2 minutes).
In 30 minutes, they will toll together 30 + 1 = 16 times.
2
Soit N le plus grand nombre qui divisera 1305, 4665 et 6905, laissant le même reste dans chaque cas. Alors la somme des chiffres en n est:
A. 4
B. 5
C. 6
D. 8
Solution:
Answer: Option A
Explanation:
N = H.C.F. of (4665 - 1305), (6905 - 4665) and (6905 - 1305)
= H.C.F. of 3360, 2240 and 5600 = 1120.
Sum of digits in N = ( 1 + 1 + 2 + 0 ) = 4
A. 9000
B. 9400
C. 9600
D. 9800
Solution
Answer: Option C
Explanation:
Greatest number of 4-digits is 9999.
L.C.M. of 15, 25, 40 and 75 is 600.
On dividing 9999 by 600, the remainder is 399.
Required number (9999 - 399) = 9600.
A) 50 jours
B) 60 jours
C) 84 jours
D) 9.333 jours
Solution:
Answer: C
Explanation:
Let 5 men can reap a field in x days
So, put the same quantities on the same side.
Men: Days
Now, Men and Days are inversely proportional to each other. If we increase the number of men fewer days will be required to complete the work.
Inversely proportional means Apti Chain Rule
Apti Chain Rule
i.e., 5: 15 = 28: x
Or, x = (28*15)/ 5
Or, x = 84 days
Hence, 5 men can reap a field in 84 days.
A) 16
B) 13/5
C) -16/3
D) 12
Solution:
Answer: C
Explanation:
Let log2√2 [1/256] = x
We know that loga y = x is similar to ax = y
So, we can write it as [1/256] = (2√2) x
Or, (2√2) x = [1/28]
Or, [21 * 21/2]x = 1/28
Or, 23x/2 = 2-8
Therefore, 3x/2 = -8
Hence, x = (-8 * 2)/ 3 = -16/3
Solution:
(6!)/(2!)(2!)=180
Solution:
You can see number less than 3! are not divisible by 8 so it decide your output
(1!+2!+3!)=9
9%8=1
1 is the answer
A. 2400
B. 2000
C. 1904
D. 1906
E. Aucun de ceux-ci
Solution:
106 x 106 - 94 x 94 = (106)2 - (94)2
= (106 + 94)(106 - 94) [Ref: (a2 - b2) = (a + b)(a - b)]
= (200 x 12)
= 2400.
La différence de deux nombres est de 1365. En divisant le plus grand nombre par le plus petit, nous obtenons 6 comme quotient et le 15 comme reste. Quel est le plus petit nombre?
A. 240
B. 270
C. 295
D. 360
Réponse: Option B
Explication:
Let the smaller number be x. Then larger number = (x + 1365).
x + 1365 = 6x + 15
5x = 1350
x = 270
Smaller number = 270
A. 1035
B. 1280
C. 2070
D. 2140
Réponse: Option A
Explication:
Let Sn =(1 + 2 + 3 + ... + 45). This is an A.P. in which a =1, d =1, n = 45.
Sn = n [2a + (n - 1)d] = 45 x [2 x 1 + (45 - 1) x 1] = 45 x 46 = (45 x 23)
2 2 2
= 45 x (20 + 3)
= 45 x 20 + 45 x 3
= 900 + 135
= 1035.
Shorcut Method:
Sn = n(n + 1) = 45(45 + 1) = 1035.
2 2
[A] 7 heures 30 minutes
[B] 8 heures
[C] 8 heures 15 minutes
[D] 8 heures 25 minutes
Solution)
C)
Ronald 1 hr work = 32/6=16/3
Elan 1 hr work = 40/5=8
Show both work in an hr=8+16/3=40/3
Show for 110 pages it will take 110/(40/3) or (110 x 3)/40=33/4hr
Since: convert it into hr 4*8=32 1 left in 1 hr 60 min 60/4=15min
Show final answer is 8hr 15 mon
Solution:
lien vers la solution
4^x/4^x + 6^x/4^x = 9^x/4^x
Now,
1 + (3/2)^x=(3/2)^(2x)
Consider (3/2)^x=u
Then,
1 + u = u^2
Simplifying this
0 = u^2 -u -1
By solving we get
u = (1 + sqrt(5))/2
and this equal to
(1 + sqrt(5))/2 = (3/2)^x
Take log both side
and you get 1.187 approx value.
Solution:
circumference of an wheel=πd
=22/7×98
22×14
=308cm =1 revolution
distance covered
1540×100=154000
now,154000÷308
500 rotations
A. 2%
B. 2,02%
C. 4%
D. 4,04%
E. Aucun de ceux-ci
Réponse: Option D
100 cm is read as 102 cm.
∴ A1 = (100 x 100) cm2 and A2 (102 x 102) cm2
(A2 - A1) = [(102)2 - (100)2]
= (102 + 100) x (102 - 100)
= 404 cm2
∴ Percentage error
=(404100×100×100)%=4.04%
Area of the square=484cm
side-22cm
perimeter=22*4=88cm
circumfrence of cirlce is 2*pi*r=88
r=14cm
area=pi*r*r=616cm^2
Solution
P(A)=1/9
P(B)=1/6
P(C)=26/36=13/18
Apply GP
you get 2/5 ans