En agua, la dirección a lo largo de la corriente se llama aguas abajo. Y, la dirección contra la corriente se llama ascendente.
Si la velocidad de un bote en agua fija es u km/hr y la velocidad de la corriente es v km/hr, entonces:
Velocidad aguas abajo = (u + v) km/hr.
Speed Upstream = (U - V) km/hr.
Si la velocidad aguas abajo es un km/hr y la velocidad aguas arriba es b km/hr, entonces:
Velocidad en agua fija = 1/2*(a + b) km/h.
Tasa de flujo = 1/2*(a - b) km/h.
Ganancias, p = sp - cp; SP> CP
Pérdida, L = CP - SP; CP> SP
P% = (P/CP) x 100
L% = (l/cp) x 100
Sp = {(100 + p%)/100} x CP
Sp = {(100 - l%)/100} x CP
Cp = {100/(100 + p%)} x sp
Cp = {100/(100 - l%)} x sp
Descuento = MP - SP
SP = MP -DISCOU
Para un peso falso , el porcentaje de ganancias será p% = (peso verdadero - peso falso/ peso falso) x 100 .
Cuando hay dos ganancias exitosas dicen m% y n%, entonces el porcentaje neto de ganancias es igual a (m+n+mn)/100
Cuando la ganancia es m% y la pérdida es n%, entonces el% de ganancias o pérdidas será: (MN-MN)/100
Si un producto se vende a m% de ganancia y luego se vende nuevamente a n% ganancias , entonces el precio de costo real del producto será: CP = [100 x 100 x p/(100+m) (100+n)] . En caso de pérdida , cp = [100 x 100 x p/(100 m) (100-n)]
Si p% y l% son iguales, entonces, p = l y % pérdida = p^2/100

Para verificar multiplicar el número por 5 o 2 y el número agregue (si mul por 5) de lo contrario si mul por 2 (reste) a través del número de izquierda
por ejemplo: 532 div por 7
Paso 1- Mul 2x5 = 10 Paso 2- Descuórate el dígito unitario y agregue al número izquierdo 53 | 2+10 = 63
Verifique el número Divisible si es que el número original también es divisible.
Similar multiplíquelo por 2 y en su lugar suma.
Multiplique el dígito unitario por 5 y sustrado ese valor multiplicado con el dígito REST si este número múltiple que el número es divisible por 17.
por ejemplo: 272 IV por 17
Paso 1-
mul 2*5 = 10 ** Paso 2- **
27-10 = 17 17 es divisorio por 17, por lo tanto, 272 es divisorio por 17.


La cara o la esfera del reloj es un círculo cuya circunferencia se divide en 60 partes iguales, llamadas espacios minuciosos.
Hour Hand y Minute Hand, un reloj tiene dos manos. La mano más pequeña se llama mano de hora o mano corta y la más grande se llama mano de minuto o mano larga.
En 60 minutos, el minuto de mano gana espacios de 55 minutos durante la mano de la hora.
(En 60 minutos, la mano de la hora se moverá 5 minutos, mientras que la mano del minuto se moverá de 60 minutos. En efecto, la ganancia espacial de la mano de minuto con respecto a la mano de la hora será de 60 - 5 = 55 minutos).
Ambas manos de un reloj coinciden una vez cada hora.
Las manos de un reloj están en la misma línea recta cuando son coincidentes o opuestos entre sí.
Cuando las dos manos de un reloj están en ángulo recto , están separados de 15 minutos .
Cuando las manos de un reloj están en direcciones opuestas, están separados a 30 minutos.
Ángulo rastreado por la mano de la hora en 12 horas = 360 °
Ángulo rastreado por minuto en 60 min. = 360 ° .
Theta (también conocido como grado) = 30 x h- (11/2) xm
Ángulo de refugio = 360 - theta
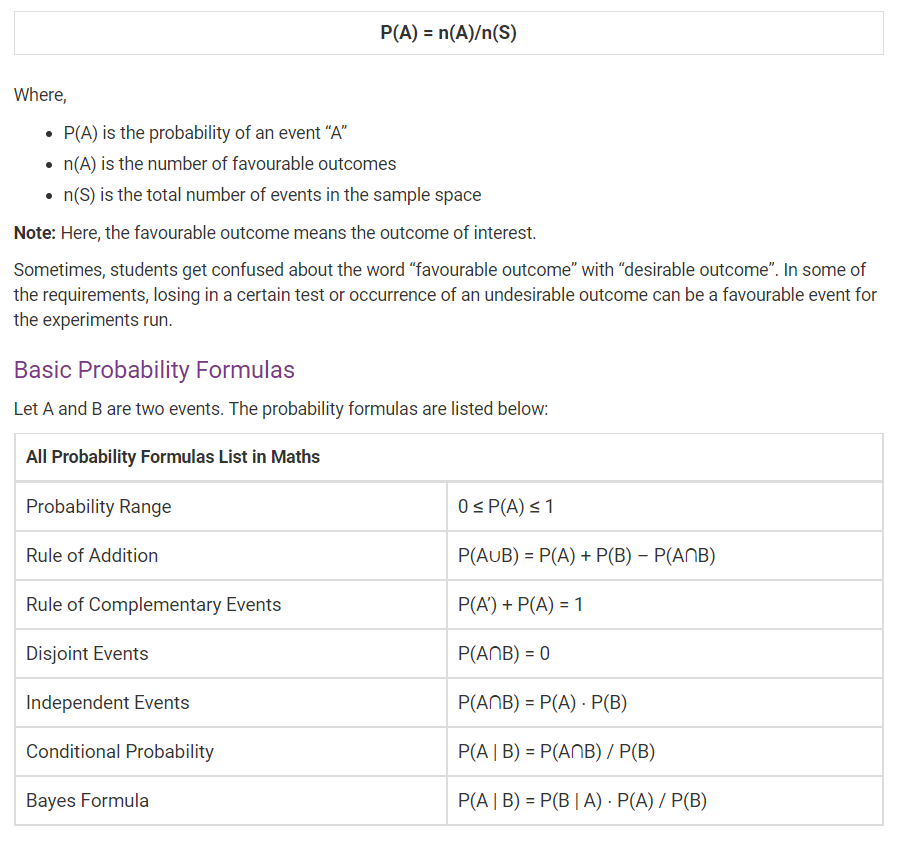


1. Números naturales (n) = 1, 2, 3 ,. . . . 2. Números enteros (w) = 0, 1, 2, 3 ,. . . . 3. Intezers (z) = −∞. . . −2, −1, 0, 1, 2, 3 ,. . . 4. Números racionales (Q) = Los números de la forma P⁄Q donde Q ≠ 0. Eg: 1⁄5, 0.46, 0.333333 están terminando, repitiendo . 5. Números irracionales (i) = Los números de la forma x1⁄n ≠ Intezer. También π y E también números irracionales no terminan, no se repiten .
Otros tipos de números: a. INCLUSO NÚMEROS: Números que son exactamente divisibles por 2. Estos números están en el formato de 2n. b. Números impares: números que da el resto 1 cuando se dividen por 2. Estos números están en el formato de 2n ± 1. C. Números primos: los números que son divisibles por 1 y el número en sí mismo son primos. El menor primo es 2. D. Números compuestos: cuyos números son divisibles por más de 2 números.
impar ± impar = par;
incluso ± par = incluso;
incluso ± impar = impar
impar × impar = impar;
incluso × incluso = incluso;
incluso × impar = incluso.
impar (cualquier número) = impar
incluso (cualquier número) = incluso
(a - b) 2 = (a2 + b2 - 2ab)
(a + b) 2 = (a2 + b2 + 2ab)
(A + B) (A - B) = (A2 - B2)
(A3 + B3) = (A + B) (A2 - AB + B2)
(A3 - B3) = (A - B) (A2 - AB + B2)
(A + B + C) 2 = A2 + B2 + C2 + 2 (AB + BC + CA)
(A3 + B3 + C3 - 3ABC) = (A + B + C) (AR> 2 + B2 + C2 - AB - BC - AC)
Consejos y trucos rápidos
Paso1: Al simplificar las expresiones dadas, los primeros soportes deben eliminarse en el orden: '––', '()', '{}', '[]'
Paso 2: Las operaciones deben realizarse estrictamente en el orden: división, multiplicación, adición y resta
Bodmas es el atajo utilizado para recordar el procedimiento de simplificación.
B: soporte
O: orden (es decir, potencia, raíz cuadrada, etc.)
D: División (de izquierda a derecha)
M: multiplicación (de izquierda a derecha)
A: adición (de izquierda a derecha)
S: resta (de izquierda a derecha)
Paso 1: al simplificar las expresiones dadas, los primeros soportes deben eliminarse en el orden: (), {}, []
Paso 2: Las operaciones deben realizarse estrictamente en el orden: división, multiplicación, adición y resta
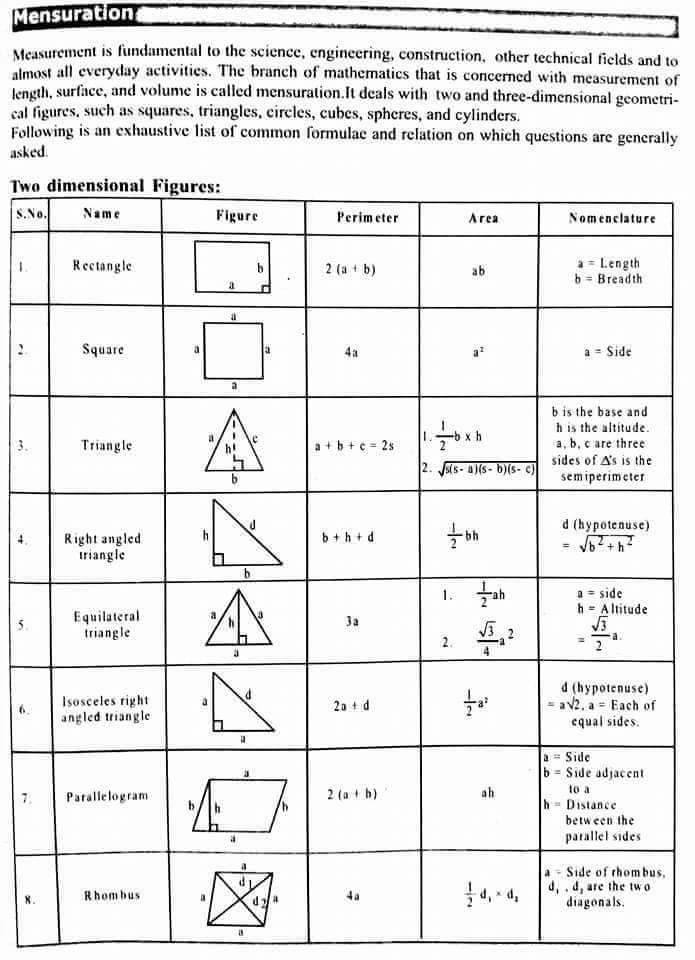
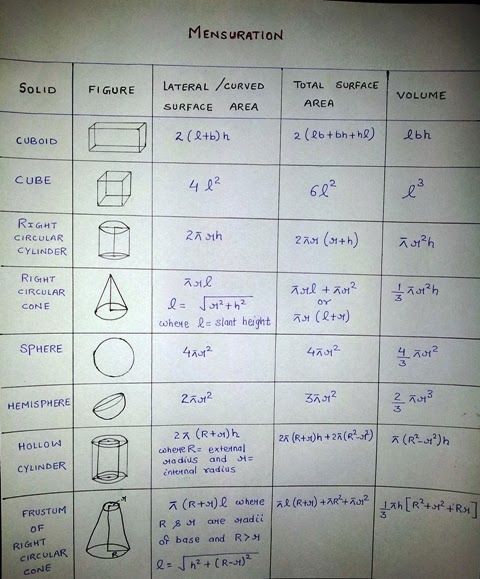
** Fórmula importante: **
Fórmula importante
Suma de cuadrado de n número natural = n (n+1) (2n+1)/2
Suma de n número natural = n (n+1)/2
Suma en ap = nx (a+l)/2
AVG de First N impar = n
AVG del primer número N par = n+1
AVG del número N Naturat = (n+1)/2
AVG de número * Número total = suma
Pregunta basada en la población
Relación y proporción
Código/decodificación
Registro
Pregunta verbal de AMCAT
Resto negativo
Prueba de elegibilidad
735/2
735/704
3/704
3/735
Solución
Option A
Find the LCM of the numerators.
LCM (147, 30) = 1470
Step 2: Find the HCF of denominators.
HCF (64, 44) = 4
So, the LCM of 147/64 and 30/44 is (LCM of Numerators) / (HCF of Denominators) = 1470 / 4 = 735/2
A) 5 mph
B) 10 mph
C) 12 mph
D) 20 mph
Solución
Option C
Let the speed of the river=x mph, then
Time taken row 30 miles upstream and 30 miles downstream = 30/(15-x) + 30/(15+x) = 9/2
= 10/(15-x) + 10/(15+x) = 3/2
= 2[10(15+x) + 10(15-x)] = 3(15-x)²
= 300 + 20x + 300 – 20x = 675 -3x²
x² = 25 or x=5
A) 3 días
B) 4 días
C) 4.5 días
D) 5.4 días
Solución
option A
Working 5 hours a day, A can complete the work in 8 days = 5*8 = 40 hours
Working 6 hours a day, B can complete the work in 10 days = 6*10 = 60 hours
(A+B)’s 1 hour’s work = (1/40+1/60)
=(3+2)/120
= 1/24
Hence, A and B can complete the work in 24 hours which is equal to 3 days.
A) 6.5 litros
B) 5 litros
C) 4 litros
D) 7.5 litros
Solución
Option B
A mixture of 40 liters of milk = 36 liters of Milk and 4 liters of water = 90:10 ratio
Now the new mixture should be in the ratio of 80:20
Hence 80% is equivalent to 36 liters (no addition of milk is done)
100% is (36/80)*100 = 45 liters of milk is present in the new mixture
Thus water shall be added= (45 – 36 – 4) = 5 liters of water
**or**

A) 12 Medianoche
B) 3 am
C) 6 am
D) 9 am
Solución
Option D
Four different devices beep after every 30 mins, 60 mins, 90 mins and 105 mins.
LCM of 30,60,90 and 105 is 1260.
Which means the devices beep together after every 1260 mins = 1260/60 = 21 hours
Hence 12 noon + 21 hours = 9 a.m
A) 21 m
B) 26 m
C) 28 m
D) 29 m
Solución
Option C
When A travels 100 m, B travels 75 m. Hence A:B = 100:75
When B travels 100 m, C travels 96 m. Hence B:C = 100:96
When B Travels 75 m, C travels (96 x 75)/100 = 72 m
Hence B:C = 75:72.
Therefore, A:B:C = 100:75:72.
So, when A Travels 100 m, C travels 72 m.
Therefore, A beat C by 28 m
A) 62
B) 68
C) 66
D) 69
Solución
Option A
70% students passed in physics = 30% failed in Physics.
65% students passed in Chemistry = 35% failed in Chemistry
Percentage of students failed in both subject = 27%.
Percentage of students failed = 35 + 30 – 27
= 38%.
Percentage of students passed = 100 – 38% = 62%
A) 40
B) 60
C) 100
D) 160
Solución
Option D
15 oxen take 80 days so, 6 oxen take x days
x = 15*80/6 = 200 days
20 oxen also take 80 day. So, 2 cows take y days
y = 20*80/2 = 800 days
Together work will be done in 800*200/(800+200) = 160 days
A) 297/10377
B) 188/121
C) 21/34
D) 33/163
Solución
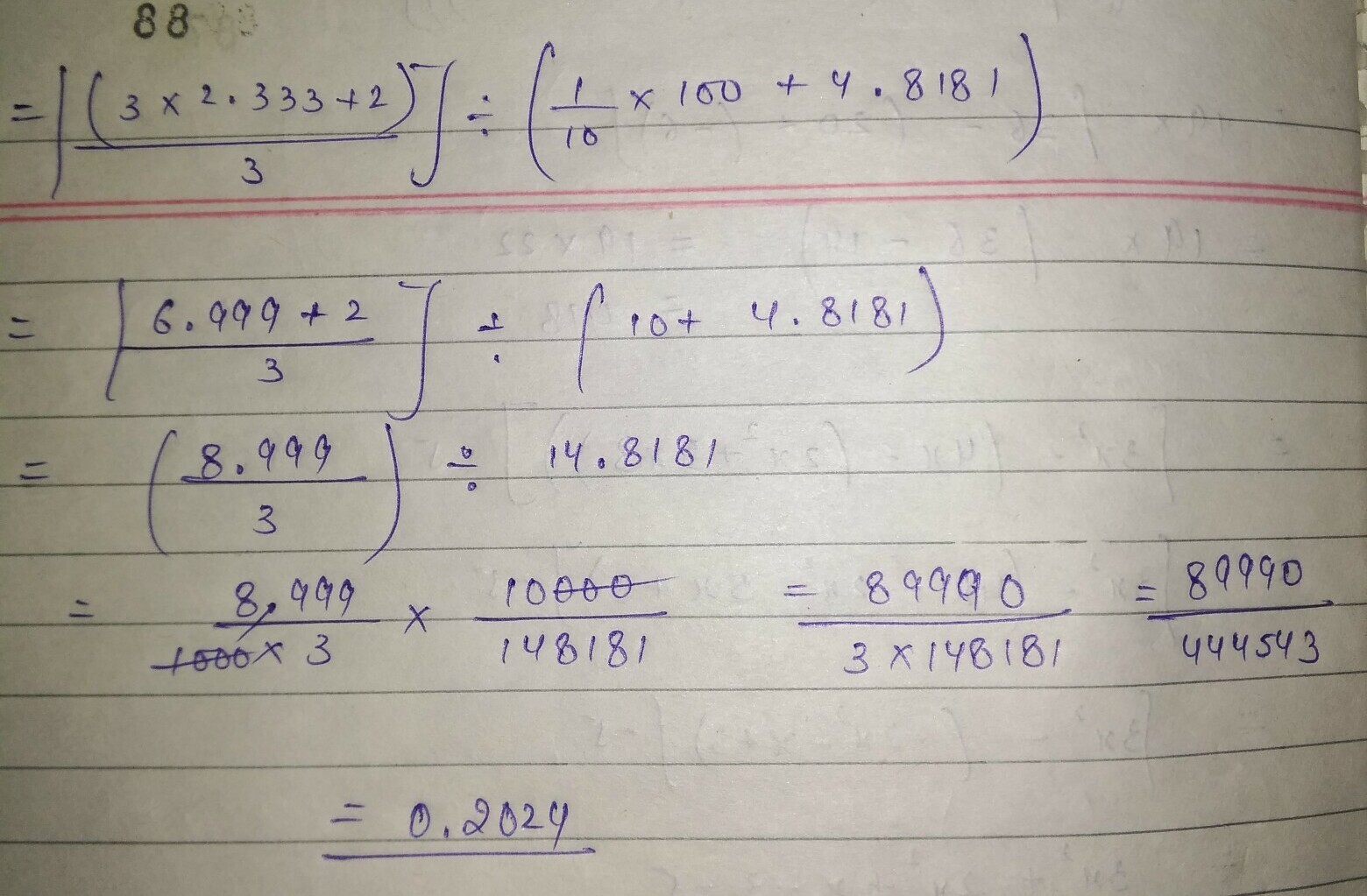
Solution: Option D
A) 6C4
B) 6p4
C) 4^6
D) 6^4
Solución
C is correct because all 4 can get 4 ticket one by one
A) 550
B) 450
C) 350
D) 150
Solución
Option B
Going through the options,
Taking Cost Price as Rs 450.
Profit = 650 – 450 = 200
Loss = 350 – 450 = 100
Clearly profit is twice the loss incurred.
Hence, Rs 450 is the correct option.
A) 7 horas 30 minutos
B) 8 horas
C) 8 horas 15 minutos
D) 8 horas 25 minutos
Solución
Option C
In 1hr, Ronald types = 32/6 pages and Elan types = 40/5 pages
If they work together they will type = 32/6 + 40/5 = 40/3 pages in 1 hr
Time needed to complete the assignment is = (3 x 110)/40 = 33/4 = 8hrs 15mins
Hence, the time required is 8 hrs 15 mins.
A) Disminución en un 20%
B) aumentó en un 20%
C) aumentó en un 10%
D) disminuyó en un 10%
Solución
Option D
Let the initial Price = Rs.100 and initial sales = 100
So, the initial revenue = Rs. 10000
Now, the price is reduced to 25% which is equal to Rs.75 and Sales is increased by 20% which is equal to 120.
Now new revenue = 120 x 75 = Rs. 9000
Change in revenue = (10000 – 9000) = Rs.1000 decrease
% decrease = (1000/10000) x 100 = 10%
Hence, the correct option is decrease of 10%.
A) 19/21
B) 3/7
C) 21/02
D) 1/3
Solución
Option A
Probability of getting atleast one nestle chocolate = [(10C1 x 5C1) + 10C2] / 15C2
[(10 x 5) + (10 x 9)/2] / [(15 x 14)/2] = 19/21.
Hence, the required probability is 19/21.
A) Rs 7490
B) Rs 7350
C) Rs 8250
D) Rs 8530
E) ninguno de estos
Solución
Option B
Solution:
Share of Anil : Share of Ruhi : Share of Teena is
2000×8 + 2600×4 : 2800×8 + 3200×4 : 4200×4
33 : 44 : 21
so share of Teena = 21/(33+44+21) × 34300 = Rs 7350
A) Rs 3200
B) Rs 4500
C) Rs 3800
D) Rs 3500
E) Rs 2800
Solución:
Option C
Solution:
Rs 3800
Solution:
(7000-x)*8*4/100 = x [ (1 + 10/100)2 – 1] + 226
70*8*4 – 32x/100 = 21x/100 + 226
2240 – 226 = 53x/100
2014 = 53x/100
So, x = Rs 3800
A) 16
B) 18
C) 12
D) 10
E) 22
Solución:
Option A
Solution:
20 men in 8 days so 16 men in 20 × 8/16 = 10 days and
25 women in 12 days so 10 women in 25 × 12/10 = 30 days
So in 3 days, they complete (1/10 + 1/30) × 3 = 2/5
So remaining work = 1 – 2/5 = 3/5
20 m 1 work in 8 days and x men 3/5 work in 6 days
So 20 × 8 × 3/5 = x × 6 × 1
So, x = 16 men
A) 3/5
B) 2/9
C) 1/8
D) 3/7
E) ninguno de estos
Solución:
Option D
Solution
Number of multiples of 3 in 140 = 140/3 = 46
Number of multiples of 7 in 140 = 140/7 = 20
Number of multiples of 3×7= 21 in 140 = 140/21 = 6
So required probability = (46+20 – 6)/140 = 60/140 = 3/7
A. Madre
B. Hermana
C. sobrina
D. tía materna
Solución C
A) A
B) B
C) C
D) E
Solución:
E
Solution:
D is father of A and grandfather of F. So, A is father of F.
Thus. D and A are the two fathers. C is the sister of F So. C is the daughter of A.
Since there is only one mother, it is evident that E is the wife of A and hence the mother of C and F.
So, B is brother of A There are three brothers. So. F is the brother of C.
Clearly, A is E's Husband.
A) Madre
B) hermana
C) tía
D) abuela
Solución:
C
Solution:
Only son of Amar's mother's father — Amar's maternal uncle.
So, the girl's maternal uncle is Arnar's maternal uncle. Thus, the girl's mother is Amar's aunt.
A) 12
B) 13
C) 14
D) 15
Solución:
A
Solution:
A+B=B+C+12
so
A=12
Solución:
P=(3*2*5)/1=30
Q=(4*2*5)/1=40
Solución:
(150+x)/15=16.
=)150+x=240
=x=90
Promedio de sus edades = suma/número =) 90/5 = 18
A. 154 °
B. 170 °
C. 160 °
D. 180 °
Solución:
We know that angle traced by hour hand in 12 hrs = 360°
From 8 to 2, there are 6 hours.
Angle traced by the hour hand in 6 hours = 6×360/12= 180°
A. 120 °
B. 125 °
C. 130 °
D. 135 °
Solución:
C
Solution:
Angle traced by hour hand in 12 hrs. = 360°.
Angle traced by it in 11/3 hrs = (360/12 x 11/3)° = 110°.
Angle traced by minute hand in 60 min. = 360°.
Angle traced by it in 40 min. = (360/60x40)°= 240°.
Required angle (240 - 110)° = 130°.
A. 3.6
B. 7.2
C. 8.4
D. 10
Solución:
B
Solution:
Speed =600/(5 x 60)= 2 m/sec.
Converting m/sec to km/hr (see important formulas section)
= (2 x18/5)km/hr= 7.2 km/hr.
A. 10
B. 8
C. 6
D. 4
Solución:
C
Opposite direction
speed=60+6=66km/h
time=distance/speed=110/66=5/3 km/h
in m/s 5/3x18/5=6
A. 14.4 segundos
B. 15.5 segundos
C. 18.8 segundos
D. 20.2 segundos
Solución :
A
Solution :
Let length of each train be x meter.
Then, speed of 1st train = x/18m/sec
Speed of 2nd train = x/12 m/sec
Now,
When both trains cross each other, time taken
=2x/(x/18+x/12)=2x/(2x+3x)/36=(2x X 36)/5x=725=14.4seconds
767 495 359 291 257?
A. 230 B. 240 C. 250 D. 280 E. 260
Soluton:
B
Solution:
797-495=272
495-359=136
So which means it is half of previous diffrences
272/2=136
291-257=32
34/2=17
So subtract 17
257-17=240
50 67 33 84 16?
A. 101 B. 109 C. 107 D. 103 E. 201
Solución:
A
Solution:
17 is the gap once increase and than decrease follow this order you will get the answer
192
10
38
2
3
Solución:
3
Solution:
Logic is 2×1 + 1 = 3, 3 × 2 + 4 =10, 10 × 3 + 9 = 39, 39 × 4 + 16 = 172…. So in place of 38, it should be 39.
999980
999990
999984
Ninguno de estos
Solución:
Greatest six-digit number is 999999. Divide this number by 12 and get remainder as 3. Since the remainder is 3, if you subtract 3 from the number, the remaining number will be a multiple of 12. So the greatest such number will be 999999 – 3 =999996.
5000
4950
4980
4900
Ninguno de estos
Solución:
Multiples of 3 between 100 and 200 are 102, 105, 108,… ,198.
Here, the first term = 102
last term = 198
Let the number of Multiples of 3 between 100 and 200 = n
W.K.T: Arithmetic Progression Formula:
an = a1 + (n - 1)d
Where, an = last term = 198
a1 = first term = 102
d = common difference = 105 - 102 = 3
---> 198 = 102 + (n - 1) * 3
---> 198 - 102 = (n - 1) * 3
---> 96 = (n - 1) * 3
---> (n - 1) = 96/3 = 32
---> n = 32 + 1
---> n = 33
Formula:
Sum of n terms = Sn = (n/2) * (a + l)
where n = number of elements = 33
a = first term = 102
l = last term = 198
Thus, using the above formula, Sum of all natural numbers between 100 and 200 which are multiples of 3 = (33/2) * (102 + 198)
= (33/2) * 300
= 33 * 150
= 4950
A. 5, 15, 25
B. 12, 15, 18
C. 10, 15, 20
D. -10, -15, -20
Solución:
Assuming that the numbers are (a – d), a, (a + d) and their sum is 45, we get the middle number as 15. Now, the product (a – d) (a + d) = 200. Solving, we get d = 5. Therefore, the numbers are 10, 15 and 20.
Solución:
x/(y+1)=1/2
and
(x+1)/y=1
2x-y=1 ....eq (1)
x=y-1 ....eq (2)
by solving eq 1 and 2 we get
x=2 and y=3
A. 80
B. 75
C. 42
D. 53
Respuesta:
Option D
Solution:
As the Number gives a remainder of 4 when it is divided by 7, then the number must be in form of (7x + 4)
The same gives remainder 1 when it is divided 4, so the number must be in the form of {4 × (7x + 4) + 1}
Also, the number when divided by 3 gives remainder 2, thus number must be in form of [3 × {4 × (7x + 4) + 1} + 2]
Now, On simplifying,
[3 × {4 × (7x + 4) + 1} + 2]
= 84x + 53
We get the final number 53 more than a multiple of 84 Hence, if the number is divided by 84,
The remainder will be 53
A) 55/601
B) 601/55
C) 11/120
D) 120/11
Solución:
Then, a + b = 55 and ab = 5 x 120 = 600.
The required sum =1a+1b = a+bab= 55600=11120
Solución:
5
2, 3, 5, 8, 13, 20, 34
Solución:
first+second=third
follow this order you get **20** as a answer
196, 169, 144, 121, 100, 80
Solución:
80
First - Second=2
A. CMN
B. Uji
C. VIJ
D. IJT
Solución:
C
Olnie
Onilen
Noilen
Lnoeni
Onnlie
Solución:
1
a. 9 años
b. 10 años
do. 13 años
d. 15 años
Solución:
Correct Option: (c)
We have to find the population of cities A and B after x years.
Step 1: Population of city A = 68000, decreases at the rate of 1200/year
68000 – 1200x
Step 2: Population of city B = 42000, increases at the rate of 800/year
42000 + 800x
Step 3: Find after how many population of cities A and B are equal.
Population of city A = Population of city B
68000 – 1200x = 42000 + 800x
68000 – 42000 = 1200x + 800x
26000 = 2000x
x = 13
a. 28 días
b. 30 días
do. 34 días
d. 40 días
Solución:
Correct Option: (b)
Step 1: Number of days worked by the worker = 60 and he remained idle for x days. Therefore, number of days worked = (60 – x)
Step 2: Each day he was getting paid Rs. 20. Therefore, the payment received for working days = (60 – x) 20
Step 3: After subtracting the amount which he forfeited, he receives Rs. 300.
Therefore,
(60 – x) 20 – 10x = 300
1200 – 20x – 10x = 300
900 = 30x
x = 30 days
a. 11
b. 15
do. 16
d. 18
Solución:
Correct Option: (b)
Let’s the number of farmers be y.
Step 1: Find number of heads
= (50 hens + 45 goats + 8 horses + y farmers)
= (103 + y)
Step 2: Number of feet
= [(Hens 2 × 50) + (45 × 4) + (8 × 4) + (y × 2)]
= [100 + 180 + 32 + 2y]
= 312 + 2y
Step 3: Find number of farmers
(312 + 2y) – (103 + y) = 224
312 + 2y – 103 – y = 224
y = 15
A) 49500
B) 49950
C) 45000
D) 49940
Solución:
The Correct answer is (B)
Answer with explanation:
The digit 5 has two place values in the numeral, 5 * 105 = 50,000 and 5 * 101 = 50.
∴Required difference = 50000 - 50 = 49950
A) Rs. 180
B) Rs. 204
C) Rs. 210
D) Rs. 220
Solución:
Option B
CI=P(1+r/100)^t
CI=2500*(1+4/100)^2
CI=2704
So the diffrenece is 204
A) Rs. 5222.2
B) Rs. 5777.7
C) Rs. 6222.2
D) Rs. 6777.7
Solución:
Option B
80000*12/65000*6=32/13
113/32*20000=5777.7rs
A) Jueves
B) Miércoles
C) Viernes
D) Domingo
Solución:
The correct option is (B)
Explanation:
The year 1996 is divisible by 4, so it is a leap year with 2 odd days.
As per the question, the first day of the year 1996 was Monday, so the first day of the year 1997 must be two days after Monday. So, it was Wednesday.
A) 1.5 km/hr
B) 2 km/hr
C) 2.5 km/hr
D) 1 km/hr
Solución:
The correct answer is B
Answer with explanation:
Let the speed of stream = X km/hr
Speed of boat = 5 km/hr
Speed upstream = 3km/hr
Apply formula: Speed upstream = speed of boat - speed of stream
∴ 3 = 5 - X
X = 5 - 3 = 2 km/hr
A) 24
B) 22
C) 23
D) 21
Solución:
The Correct answer is (B)
Explanation:
The hands of a clock coincide only once between 11 O' clock and 1 O' clock, so in every 12 hours, the hands of a clock will coincide for 11 times.
∴ In a day or 24 hours, the hands of a clock will coincide for 22 (11+11) times.
A) 10 horas
B) 12 horas
C) 14 horas
D) 16 horas
Solución:
Option B
Water enter in 1 hr=1/6
Water empty in 1 hr=1/12
net=1/6-1/12=1/12
or 12hr
A) 8.5 km/s
B) 7.5 km/s
C) 9.5 km/s
D) 6.5 km/s
Solución:
Option B
sec=4*60=240s
speed=500/240=25/12m/s
in km/s speed is =25/12*18/5=7.5km/s.
Solución:
Surface area of cube=6a^2
600=6*a^2
a=10
diagonal of cube=sqrt(3)*a
ans=sqrt(3)*10
El HCF de dos números es 23 y los otros dos factores de su LCM son 13 y 14. El mayor de los dos números es:
A. 276
B. 299
C. 322
D. 345
Solución:
Answer: Option C
Explanation:
Clearly, the numbers are (23 x 13) and (23 x 14).
Larger number = (23 x 14) = 322.
Seis campanas comienzan el peaje y el peaje a intervalos de 2, 4, 6, 8 10 y 12 segundos respectivamente. En 30 minutos, ¿cuántas veces dan un precio juntos?
A. 4
B. 10
C. 15
D. 16
Solución:
Answer: Option D
Explanation:
L.C.M. of 2, 4, 6, 8, 10, 12 is 120.
So, the bells will toll together after every 120 seconds(2 minutes).
In 30 minutes, they will toll together 30 + 1 = 16 times.
2
Sea n el mayor número que dividirá 1305, 4665 y 6905, dejando el mismo resto en cada caso. Entonces la suma de los dígitos en n es:
A. 4
B. 5
C. 6
D. 8
Solución:
Answer: Option A
Explanation:
N = H.C.F. of (4665 - 1305), (6905 - 4665) and (6905 - 1305)
= H.C.F. of 3360, 2240 and 5600 = 1120.
Sum of digits in N = ( 1 + 1 + 2 + 0 ) = 4
A. 9000
B. 9400
C. 9600
D. 9800
Solución
Answer: Option C
Explanation:
Greatest number of 4-digits is 9999.
L.C.M. of 15, 25, 40 and 75 is 600.
On dividing 9999 by 600, the remainder is 399.
Required number (9999 - 399) = 9600.
A) 50 días
B) 60 días
C) 84 días
D) 9.333 días
Solución:
Answer: C
Explanation:
Let 5 men can reap a field in x days
So, put the same quantities on the same side.
Men: Days
Now, Men and Days are inversely proportional to each other. If we increase the number of men fewer days will be required to complete the work.
Inversely proportional means Apti Chain Rule
Apti Chain Rule
i.e., 5: 15 = 28: x
Or, x = (28*15)/ 5
Or, x = 84 days
Hence, 5 men can reap a field in 84 days.
A) 16
B) 13/5
C) -16/3
D) 12
Solución:
Answer: C
Explanation:
Let log2√2 [1/256] = x
We know that loga y = x is similar to ax = y
So, we can write it as [1/256] = (2√2) x
Or, (2√2) x = [1/28]
Or, [21 * 21/2]x = 1/28
Or, 23x/2 = 2-8
Therefore, 3x/2 = -8
Hence, x = (-8 * 2)/ 3 = -16/3
Solución:
(6!)/(2!)(2!)=180
Solución:
You can see number less than 3! are not divisible by 8 so it decide your output
(1!+2!+3!)=9
9%8=1
1 is the answer
A. 2400
B. 2000
C. 1904
D. 1906
E. Ninguno de estos
Solución:
106 x 106 - 94 x 94 = (106)2 - (94)2
= (106 + 94)(106 - 94) [Ref: (a2 - b2) = (a + b)(a - b)]
= (200 x 12)
= 2400.
La diferencia de dos números es 1365. Al dividir el número más grande por los más pequeños, obtenemos 6 como cociente y el 15 como resto. ¿Cuál es el número más pequeño?
A. 240
B. 270
C. 295
D. 360
Respuesta: Opción B
Explicación:
Let the smaller number be x. Then larger number = (x + 1365).
x + 1365 = 6x + 15
5x = 1350
x = 270
Smaller number = 270
A. 1035
B. 1280
C. 2070
D. 2140
Respuesta: Opción A
Explicación:
Let Sn =(1 + 2 + 3 + ... + 45). This is an A.P. in which a =1, d =1, n = 45.
Sn = n [2a + (n - 1)d] = 45 x [2 x 1 + (45 - 1) x 1] = 45 x 46 = (45 x 23)
2 2 2
= 45 x (20 + 3)
= 45 x 20 + 45 x 3
= 900 + 135
= 1035.
Shorcut Method:
Sn = n(n + 1) = 45(45 + 1) = 1035.
2 2
[A] 7 horas 30 minutos
[B] 8 horas
[C] 8 horas 15 minutos
[D] 8 horas 25 minutos
Solución)
C)
Ronald 1 hr work = 32/6=16/3
Elan 1 hr work = 40/5=8
Show both work in an hr=8+16/3=40/3
Show for 110 pages it will take 110/(40/3) or (110 x 3)/40=33/4hr
Since: convert it into hr 4*8=32 1 left in 1 hr 60 min 60/4=15min
Show final answer is 8hr 15 mon
Solución:
enlace a la solución
4^x/4^x + 6^x/4^x = 9^x/4^x
Now,
1 + (3/2)^x=(3/2)^(2x)
Consider (3/2)^x=u
Then,
1 + u = u^2
Simplifying this
0 = u^2 -u -1
By solving we get
u = (1 + sqrt(5))/2
and this equal to
(1 + sqrt(5))/2 = (3/2)^x
Take log both side
and you get 1.187 approx value.
Solution:
circumference of an wheel=πd
=22/7×98
22×14
=308cm =1 revolution
distance covered
1540×100=154000
now,154000÷308
500 rotations
A. 2%
B. 2.02%
C. 4%
D. 4.04%
E. Ninguno de estos
Respuesta: Opción D
100 cm is read as 102 cm.
∴ A1 = (100 x 100) cm2 and A2 (102 x 102) cm2
(A2 - A1) = [(102)2 - (100)2]
= (102 + 100) x (102 - 100)
= 404 cm2
∴ Percentage error
=(404100×100×100)%=4.04%
Area of the square=484cm
side-22cm
perimeter=22*4=88cm
circumfrence of cirlce is 2*pi*r=88
r=14cm
area=pi*r*r=616cm^2
Solución
P(A)=1/9
P(B)=1/6
P(C)=26/36=13/18
Apply GP
you get 2/5 ans