torchsde下載torchsde源代碼下載

torchsde

Python

v0.2.6

下載

Pytorch實施可區分的SDE求解器

該庫提供了隨機微分方程（SDE）求解器，並具有GPU支持和有效的反向傳播。

安裝

pip install torchsde

要求： Python> = 3.8和Pytorch> = 1.6.0。

文件

在這裡可用。

例子

快速示例

 import torch
import torchsde

batch_size , state_size , brownian_size = 32 , 3 , 2
t_size = 20

class SDE ( torch . nn . Module ):
    noise_type = 'general'
    sde_type = 'ito'

    def __init__ ( self ):
        super (). __init__ ()
        self . mu = torch . nn . Linear ( state_size , 
                                  state_size )
        self . sigma = torch . nn . Linear ( state_size , 
                                     state_size * brownian_size )

    # Drift
    def f ( self , t , y ):
        return self . mu ( y )  # shape (batch_size, state_size)

    # Diffusion
    def g ( self , t , y ):
        return self . sigma ( y ). view ( batch_size , 
                                  state_size , 
                                  brownian_size )

sde = SDE ()
y0 = torch . full (( batch_size , state_size ), 0.1 )
ts = torch . linspace ( 0 , 1 , t_size )
# Initial state y0, the SDE is solved over the interval [ts[0], ts[-1]].
# ys will have shape (t_size, batch_size, state_size)
ys = torchsde . sdeint ( sde , y0 , ts )

筆記本

examples/demo.ipynb提供了有關如何求解SDE的簡短指南，包括諸如固定求解器中的隨機性和噪聲類型的選擇之類的微妙點。

潛在SDE

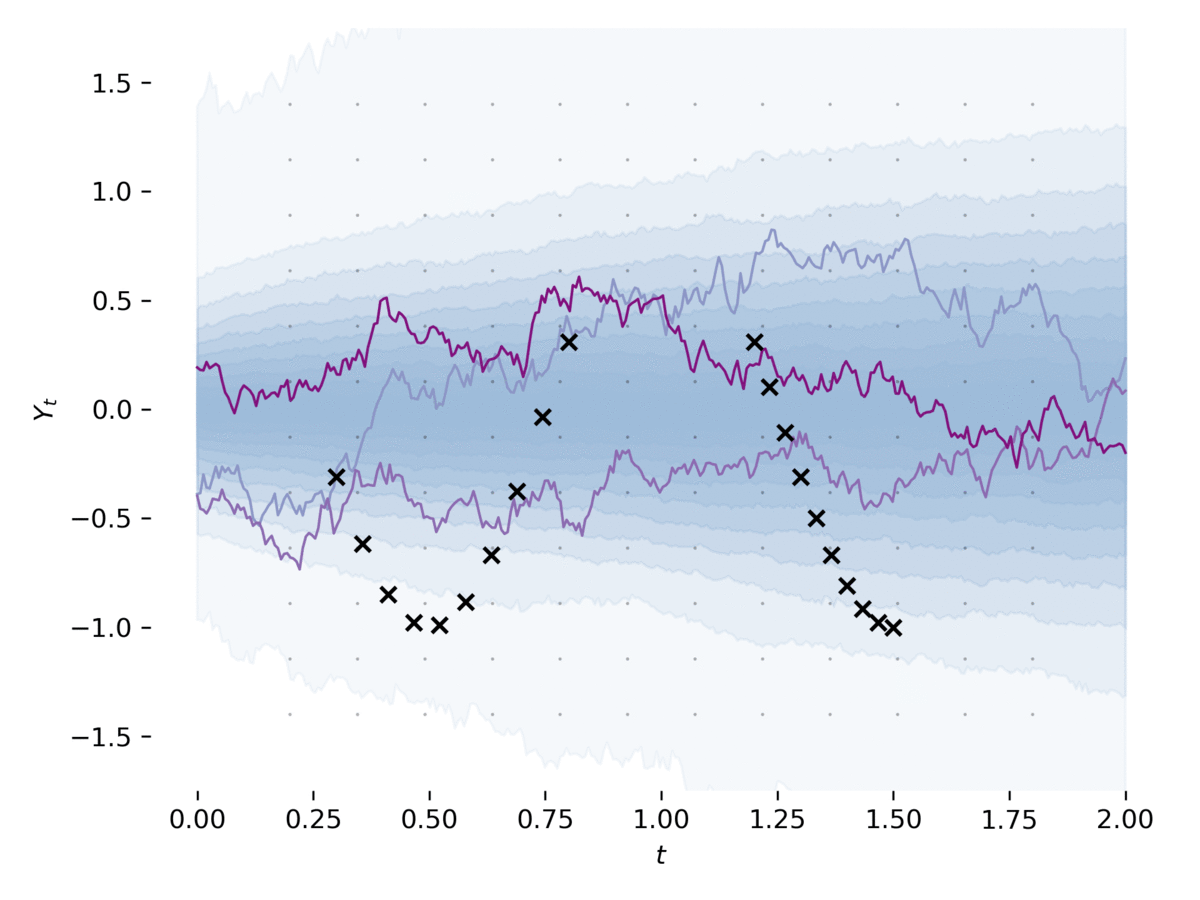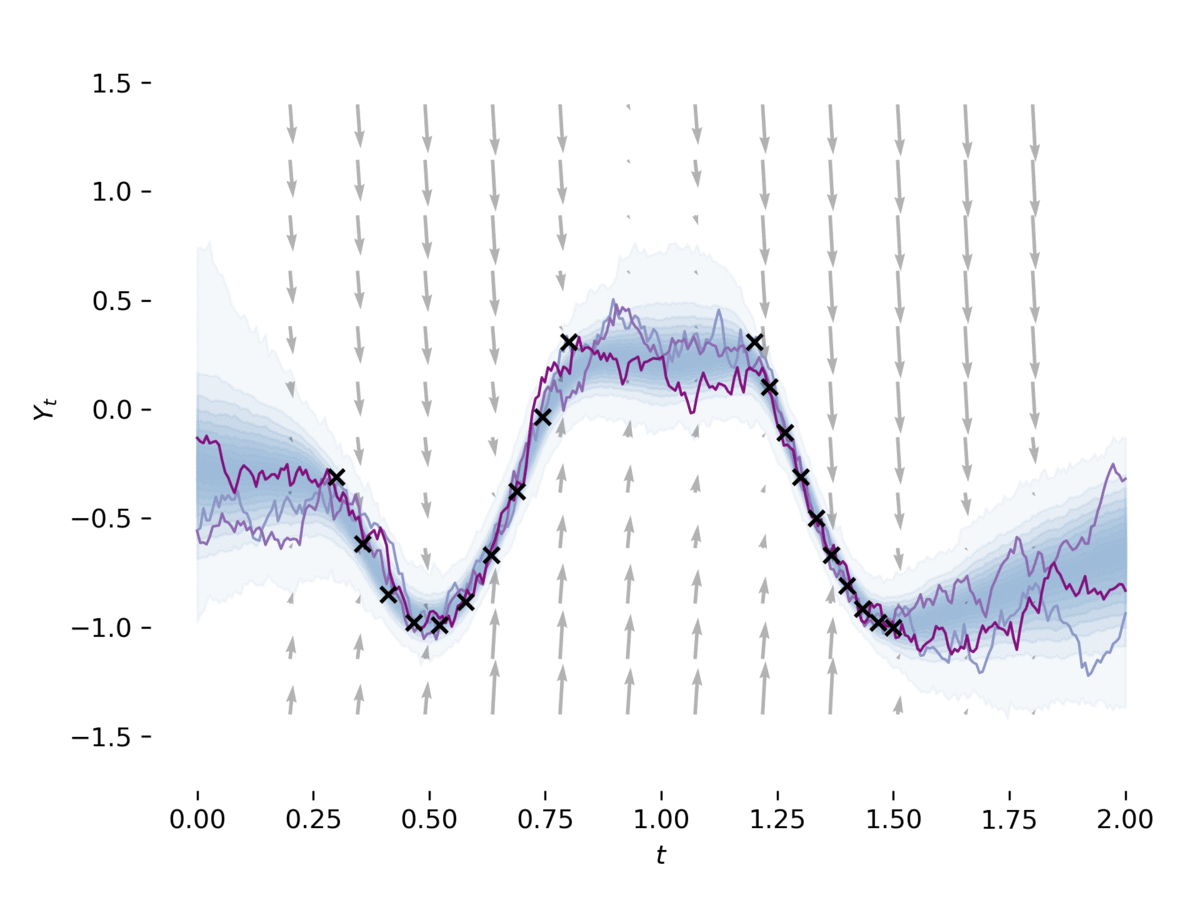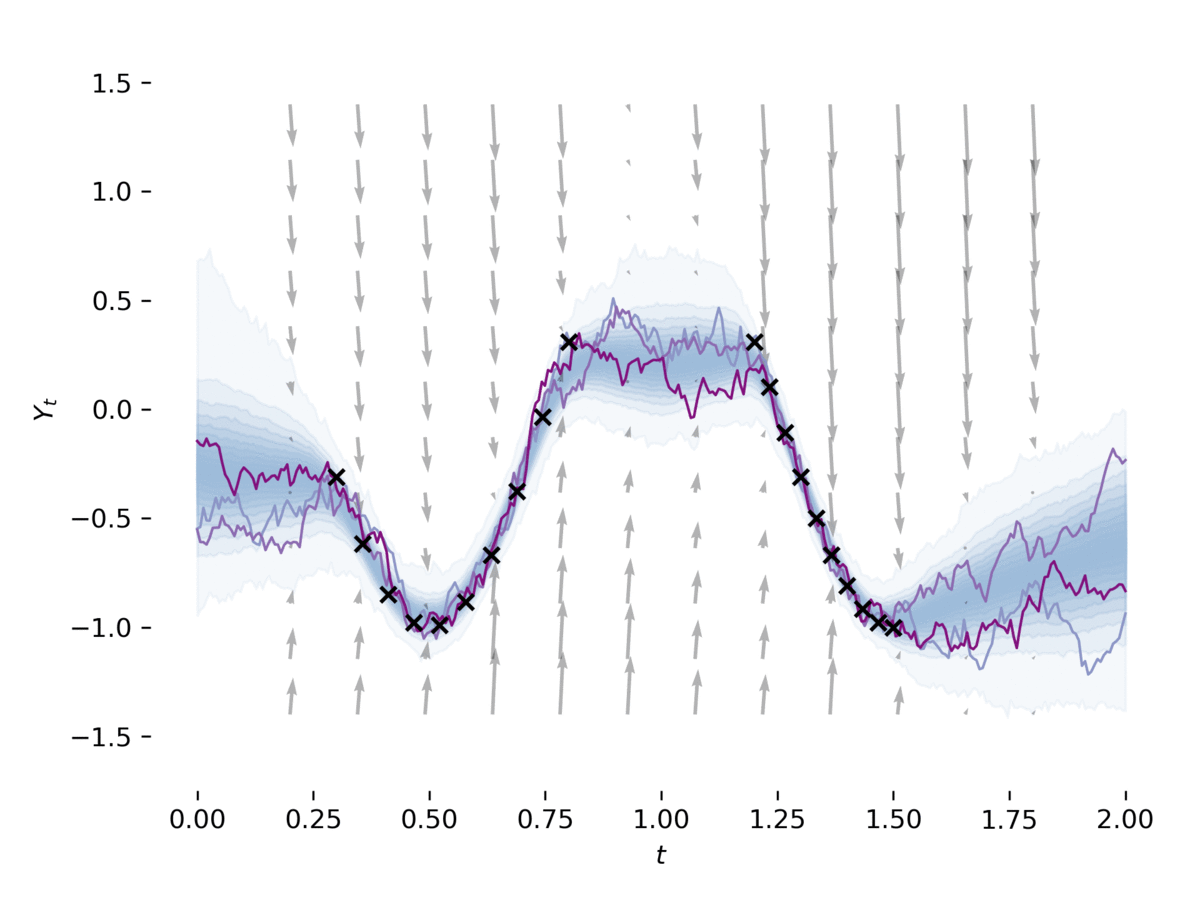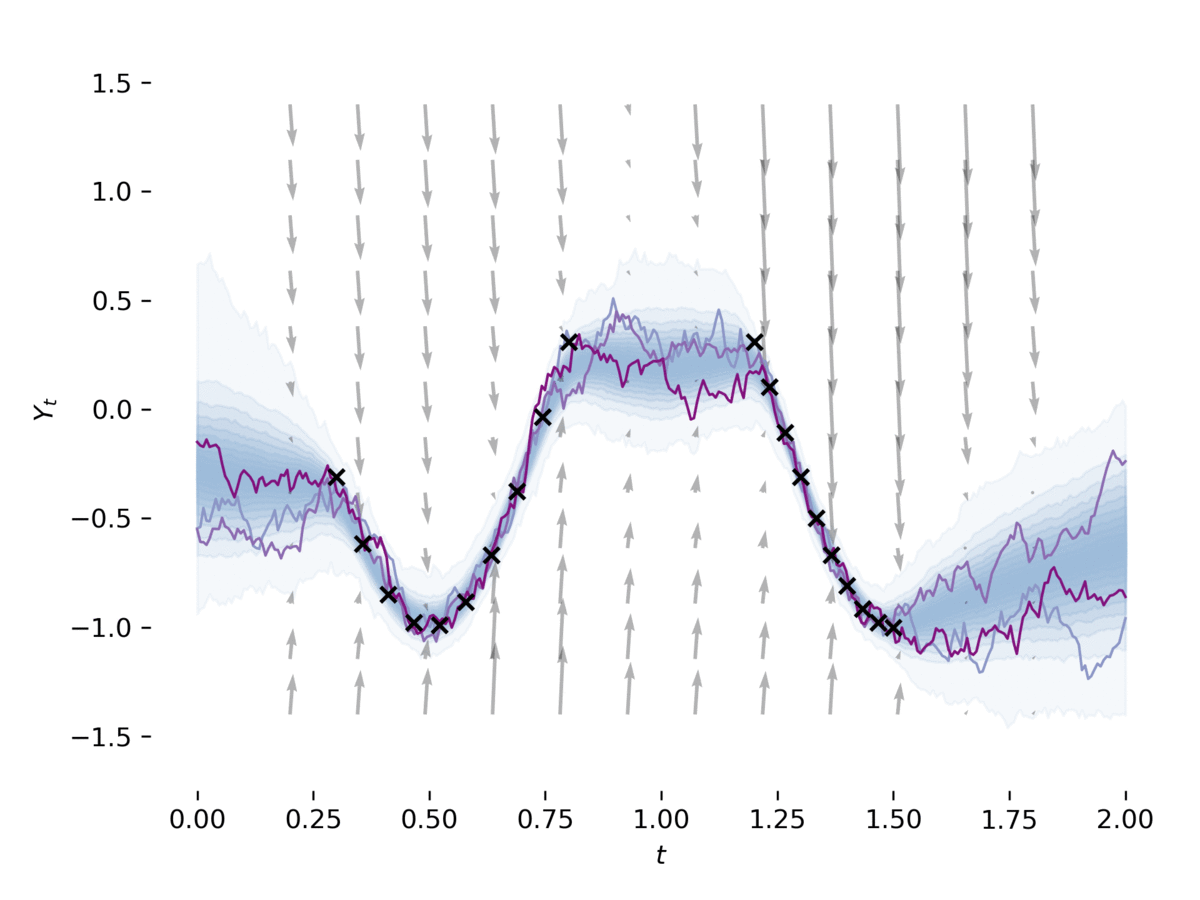
examples/latent_sde.py學習一個潛在的隨機微分方程，如[1]第5節中。該示例符合SDE的數據，同時將其正規化為像Ornstein-uhlenbeck的先前過程。該模型可以鬆散地視為具有其先前和近似後部為SDE的變異自動編碼器。這個示例可以通過

python -m examples.latent_sde --train-dir < TRAIN_DIR >

該程序將數字輸出到<TRAIN_DIR>指定的路徑。培訓應在500次迭代後使用默認的超參數穩定。

神經SDE作為gan

examples/sde_gan.py像[2]，[3]一樣，將SDE學習為gan。該示例將SDE訓練為GAN的發電機，而使用神經CDE [4]作為鑑別器。這個示例可以通過

python -m examples.sde_gan

引用

如果您發現此代碼庫在您的研究中有用，請考慮引用以下內容：

 @article{li2020scalable,
  title={Scalable gradients for stochastic differential equations},
  author={Li, Xuechen and Wong, Ting-Kam Leonard and Chen, Ricky T. Q. and Duvenaud, David},
  journal={International Conference on Artificial Intelligence and Statistics},
  year={2020}
}

 @article{kidger2021neuralsde,
  title={Neural {SDE}s as {I}nfinite-{D}imensional {GAN}s},
  author={Kidger, Patrick and Foster, James and Li, Xuechen and Oberhauser, Harald and Lyons, Terry},
  journal={International Conference on Machine Learning},
  year={2021}
}