توفر هذه المكتبة حلول المعادلة التفاضلية العشوائية (SDE) بدعم من GPU والترجمة الفعالة.
pip install torchsdeالمتطلبات: Python> = 3.8 و Pytorch> = 1.6.0.
متاح هنا.
import torch
import torchsde
batch_size , state_size , brownian_size = 32 , 3 , 2
t_size = 20
class SDE ( torch . nn . Module ):
noise_type = 'general'
sde_type = 'ito'
def __init__ ( self ):
super (). __init__ ()
self . mu = torch . nn . Linear ( state_size ,
state_size )
self . sigma = torch . nn . Linear ( state_size ,
state_size * brownian_size )
# Drift
def f ( self , t , y ):
return self . mu ( y ) # shape (batch_size, state_size)
# Diffusion
def g ( self , t , y ):
return self . sigma ( y ). view ( batch_size ,
state_size ,
brownian_size )
sde = SDE ()
y0 = torch . full (( batch_size , state_size ), 0.1 )
ts = torch . linspace ( 0 , 1 , t_size )
# Initial state y0, the SDE is solved over the interval [ts[0], ts[-1]].
# ys will have shape (t_size, batch_size, state_size)
ys = torchsde . sdeint ( sde , y0 , ts ) examples/demo.ipynb تقدم دليلًا قصيرًا حول كيفية حل SDEs ، بما في ذلك النقاط الدقيقة مثل إصلاح العشوائية في المحاليل واختيار أنواع الضوضاء .
examples/latent_sde.py يتعلم معادلة تفاضلية عشوائية كامنة ، كما في القسم 5 من [1]. المثال يناسب SDE للبيانات ، مع تنظيمها ليكون مثل عملية ornstein-uhlenbeck السابقة. يمكن النظر إلى النموذج بشكل فضفاض على أنه مشفر تلقائي مختلف مع وجوده الخلفي السابق والتقريبي. يمكن تشغيل هذا المثال عبر
python -m examples.latent_sde --train-dir < TRAIN_DIR > يقوم البرنامج بإخراج أرقام المسار المحدد بواسطة <TRAIN_DIR> . يجب أن يستقر التدريب بعد 500 تكرار مع فرط الأبرامير الافتراضي.
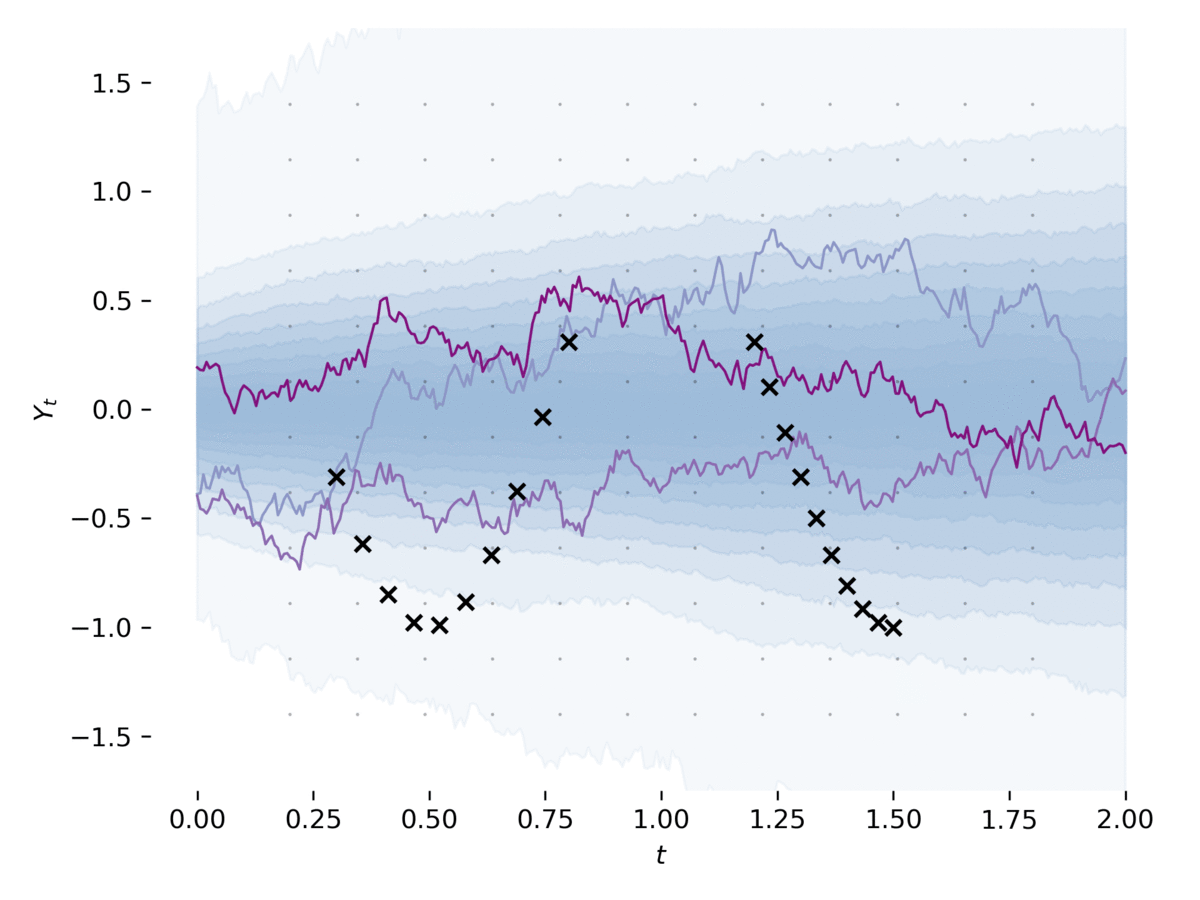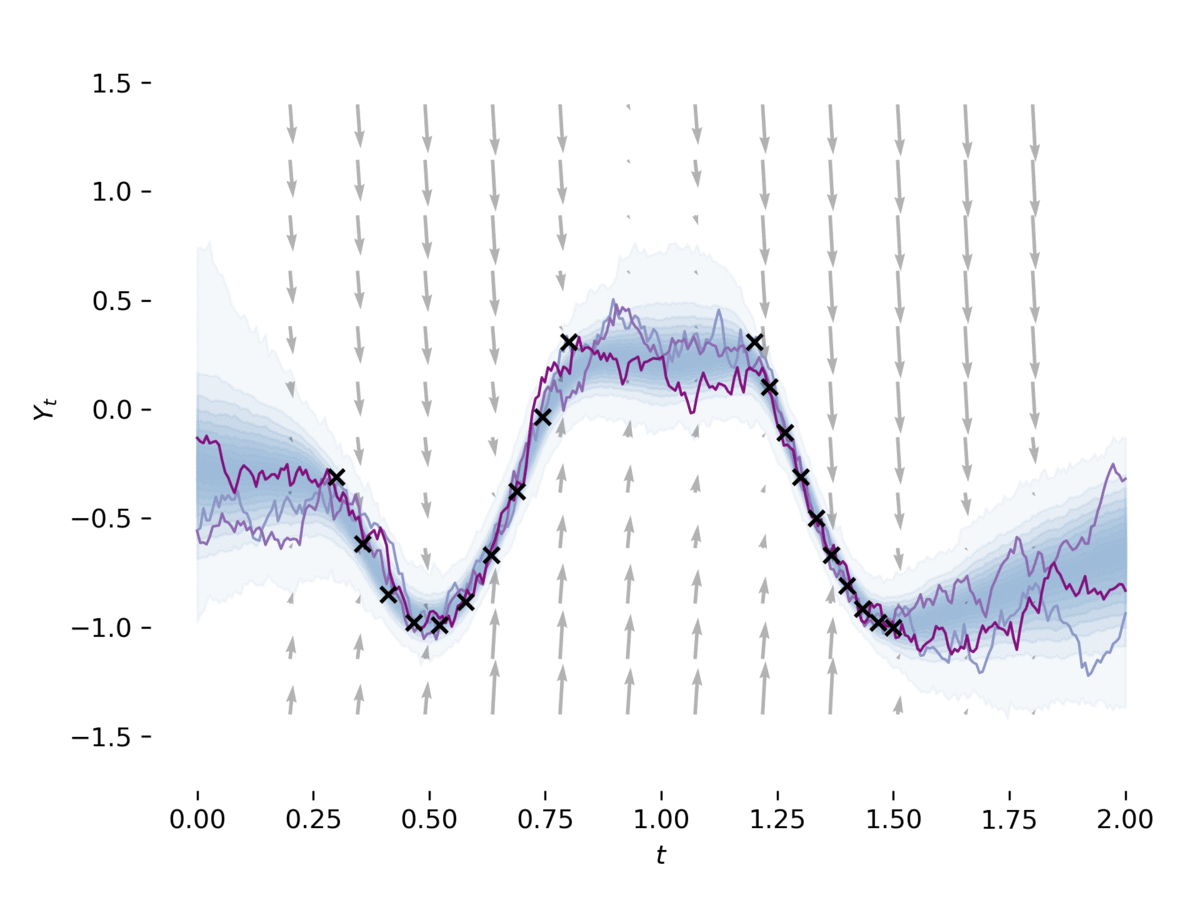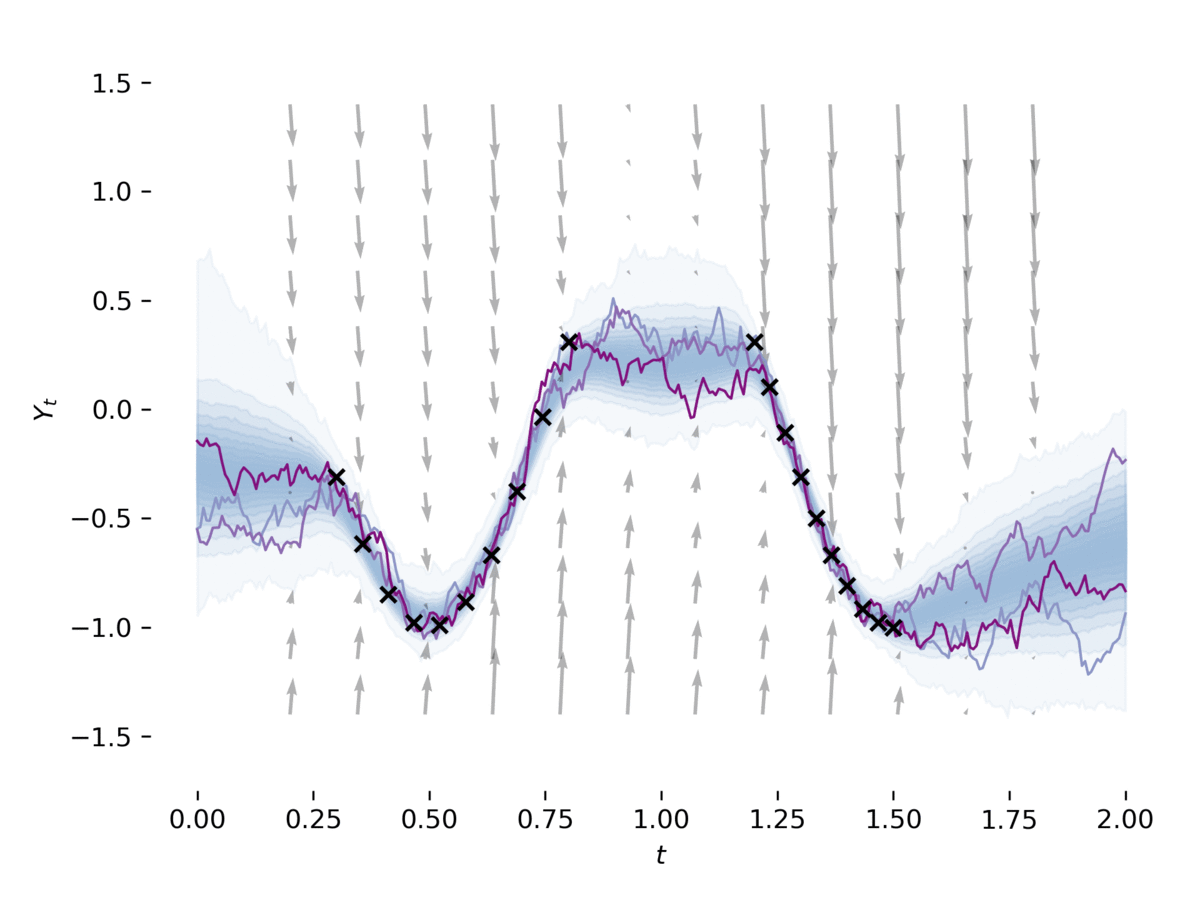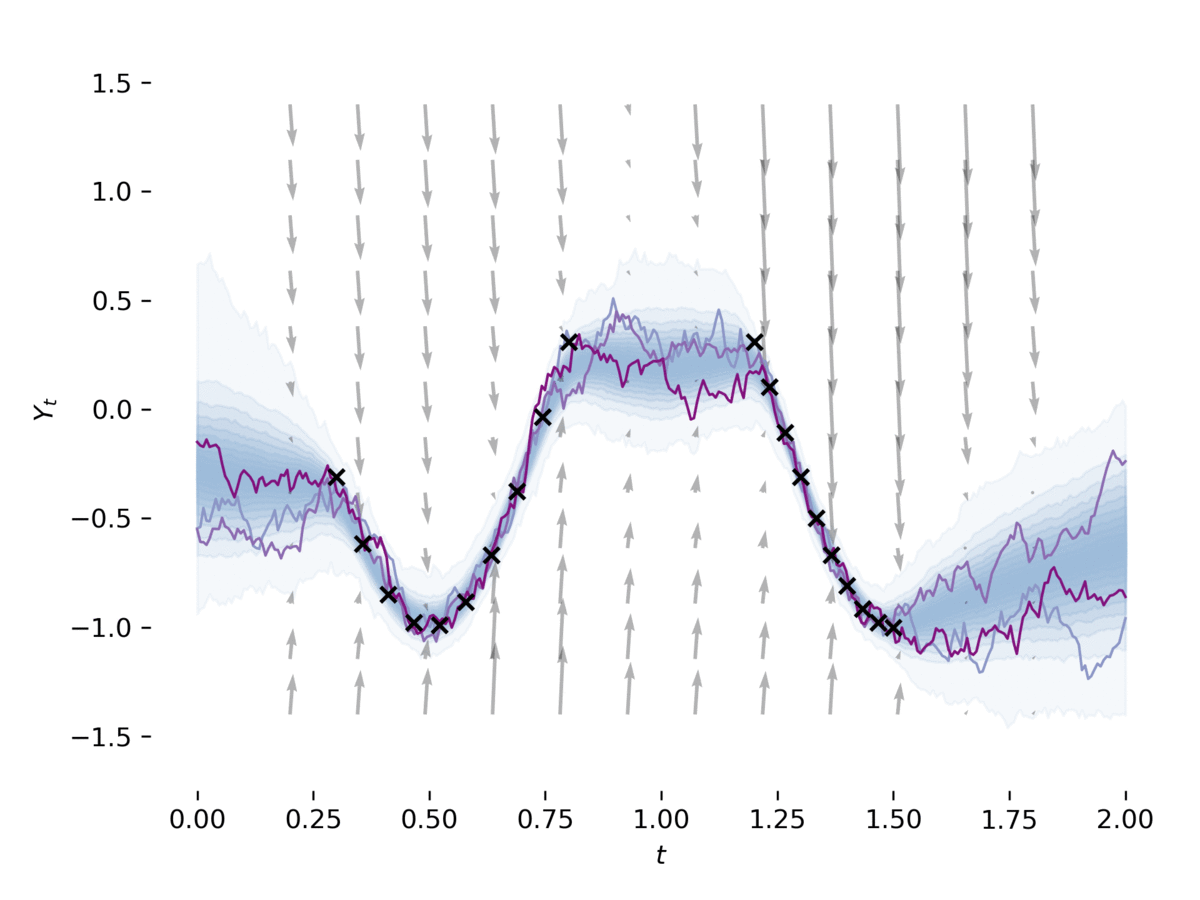
examples/sde_gan.py يتعلم SDE كـ GAN ، كما في [2] ، [3]. يدرب المثال SDE كمولد لـ GAN ، مع استخدام CDE العصبي [4] باعتباره التمييز. يمكن تشغيل هذا المثال عبر
python -m examples.sde_ganإذا وجدت قاعدة الشفرة هذه مفيدة في بحثك ، فيرجى التفكير في الاستشهاد أو كليهما:
@article{li2020scalable,
title={Scalable gradients for stochastic differential equations},
author={Li, Xuechen and Wong, Ting-Kam Leonard and Chen, Ricky T. Q. and Duvenaud, David},
journal={International Conference on Artificial Intelligence and Statistics},
year={2020}
}
@article{kidger2021neuralsde,
title={Neural {SDE}s as {I}nfinite-{D}imensional {GAN}s},
author={Kidger, Patrick and Foster, James and Li, Xuechen and Oberhauser, Harald and Lyons, Terry},
journal={International Conference on Machine Learning},
year={2021}
}
[1] Xuechen LI ، Ting-kam Leonard Wong ، Ricky TQ Chen ، David Duvenaud. "التدرجات القابلة للتطوير للمعادلات التفاضلية العشوائية". المؤتمر الدولي للذكاء الاصطناعي والإحصاء. 2020. [Arxiv]
[2] باتريك كيدجر ، جيمس فوستر ، شويشن لي ، هارالد أوبرهاوزر ، تيري ليون. "SDEs العصبية مثل خانس لا حصر لها الأبعاد". المؤتمر الدولي للتعلم الآلي 2021. [Arxiv]
[3] باتريك كيدجر ، جيمس فوستر ، شويشن لي ، تيري ليون. "تدرجات فعالة ودقيقة ل SDEs العصبية". 2021. [Arxiv]
[4] باتريك كيدجر ، جيمس موريل ، جيمس فوستر ، تيري ليون ، "المعادلات التفاضلية التي تسيطر عليها العصبية لسلسلة زمنية غير منتظمة". أنظمة معالجة المعلومات العصبية 2020. [Arxiv]
هذا مشروع بحثي ، وليس منتج Google الرسمي.