torchsde

Реализация Pytorch дифференцируемых решателей SDE

Эта библиотека обеспечивает решатели стохастических дифференциальных уравнений (SDE) с поддержкой графических процессоров и эффективным обратным распространением.

---

Установка

pip install torchsde

Требования: Python> = 3,8 и Pytorch> = 1,6,0.

Документация

Доступно здесь.

Примеры

Быстрый пример

 import torch
import torchsde

batch_size , state_size , brownian_size = 32 , 3 , 2
t_size = 20

class SDE ( torch . nn . Module ):
    noise_type = 'general'
    sde_type = 'ito'

    def __init__ ( self ):
        super (). __init__ ()
        self . mu = torch . nn . Linear ( state_size , 
                                  state_size )
        self . sigma = torch . nn . Linear ( state_size , 
                                     state_size * brownian_size )

    # Drift
    def f ( self , t , y ):
        return self . mu ( y )  # shape (batch_size, state_size)

    # Diffusion
    def g ( self , t , y ):
        return self . sigma ( y ). view ( batch_size , 
                                  state_size , 
                                  brownian_size )

sde = SDE ()
y0 = torch . full (( batch_size , state_size ), 0.1 )
ts = torch . linspace ( 0 , 1 , t_size )
# Initial state y0, the SDE is solved over the interval [ts[0], ts[-1]].
# ys will have shape (t_size, batch_size, state_size)
ys = torchsde . sdeint ( sde , y0 , ts )

Блокнот

examples/demo.ipynb дают краткое руководство о том, как решить SDE, включая тонкие точки, такие как исправление случайности в решателе и выбор типов шума .

Скрытый SDE

examples/latent_sde.py изучают скрытое стохастическое дифференциальное уравнение , как в разделе 5 из [1]. Пример подходит для данных SDE, в то же время регулярируя его как предыдущий процесс Ornstein-Uhlenbeck. Модель может быть свободно рассматривать как вариационный автоэкодер с его предыдущим и приблизительным задним, представляющим SDES. Этот пример можно запустить через

python -m examples.latent_sde --train-dir < TRAIN_DIR >

Программа выводит цифры на путь, указанный <TRAIN_DIR> . Обучение должно стабилизироваться после 500 итераций с гиперпараметрами по умолчанию.

Нейронные SDE как Ганс

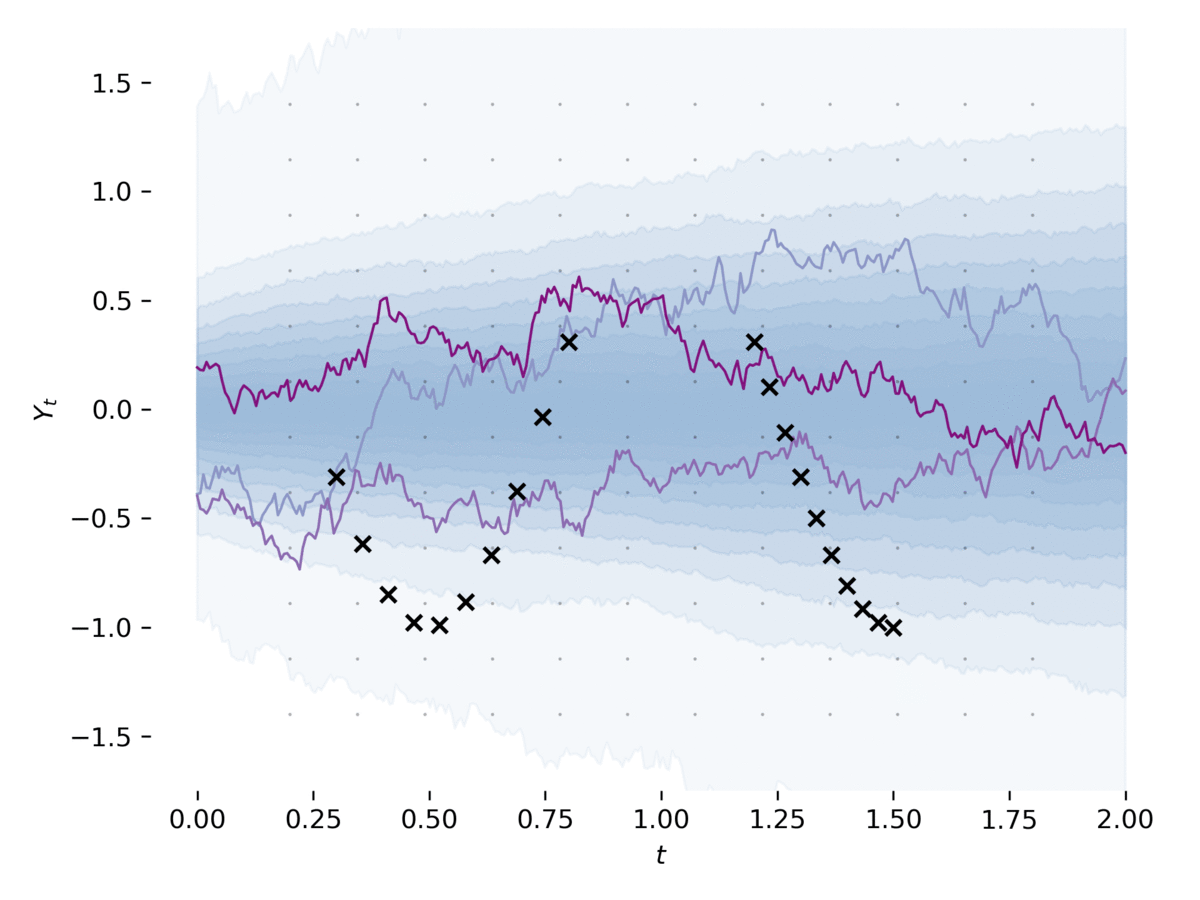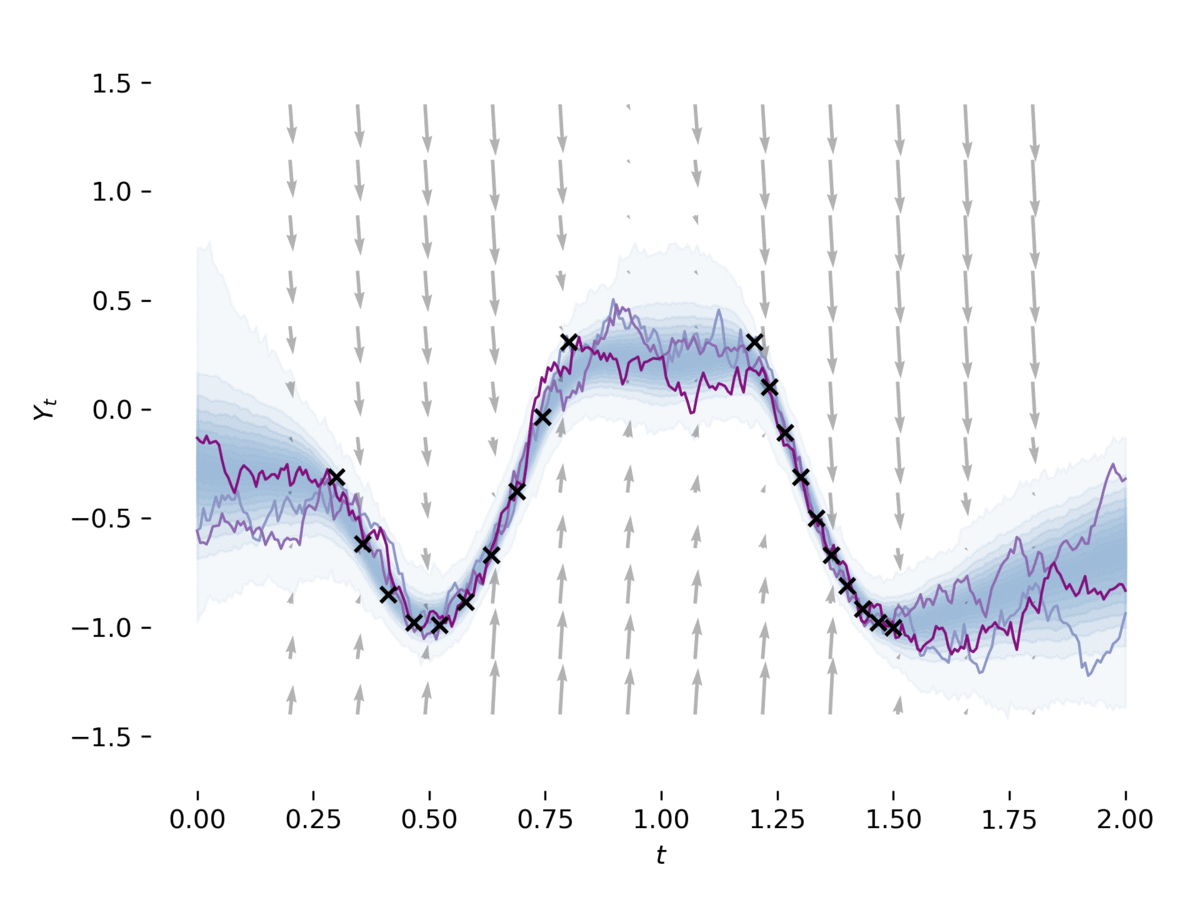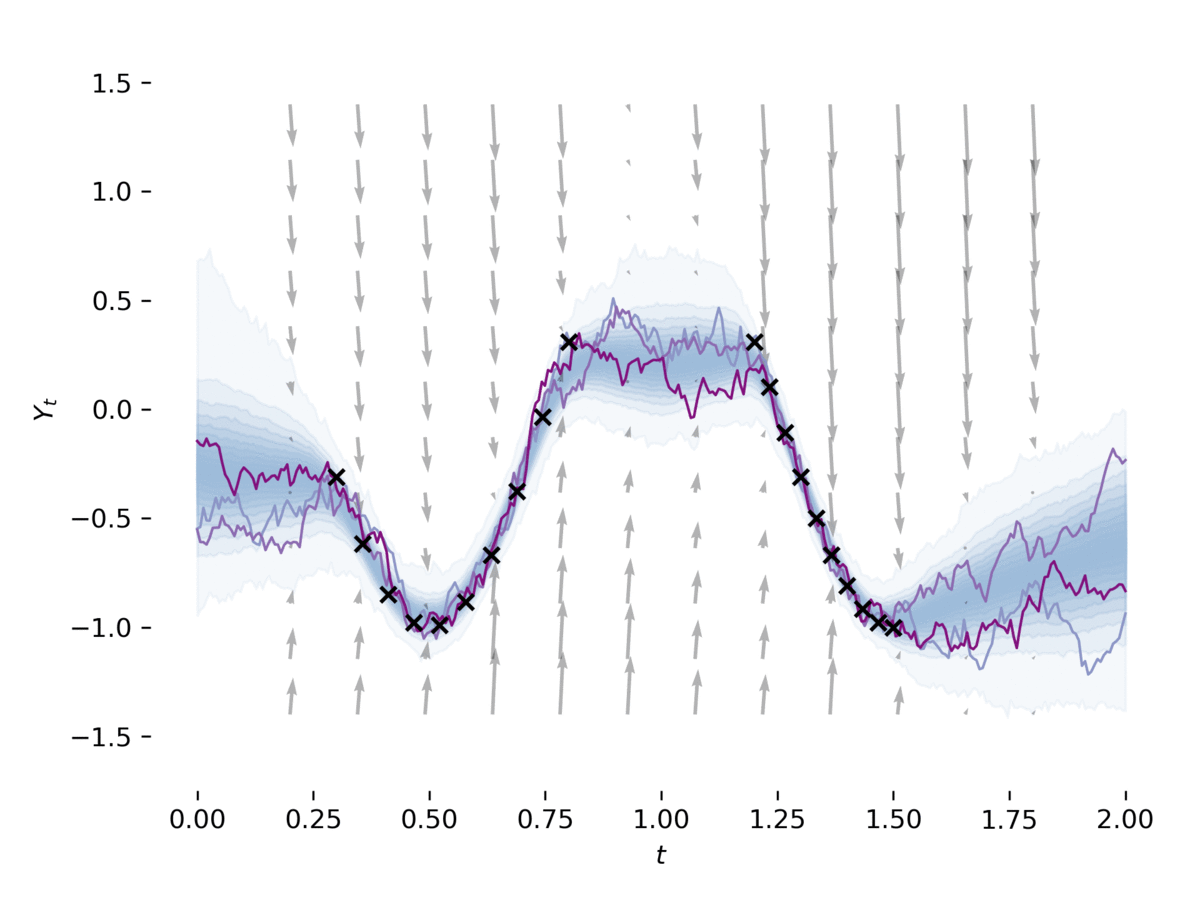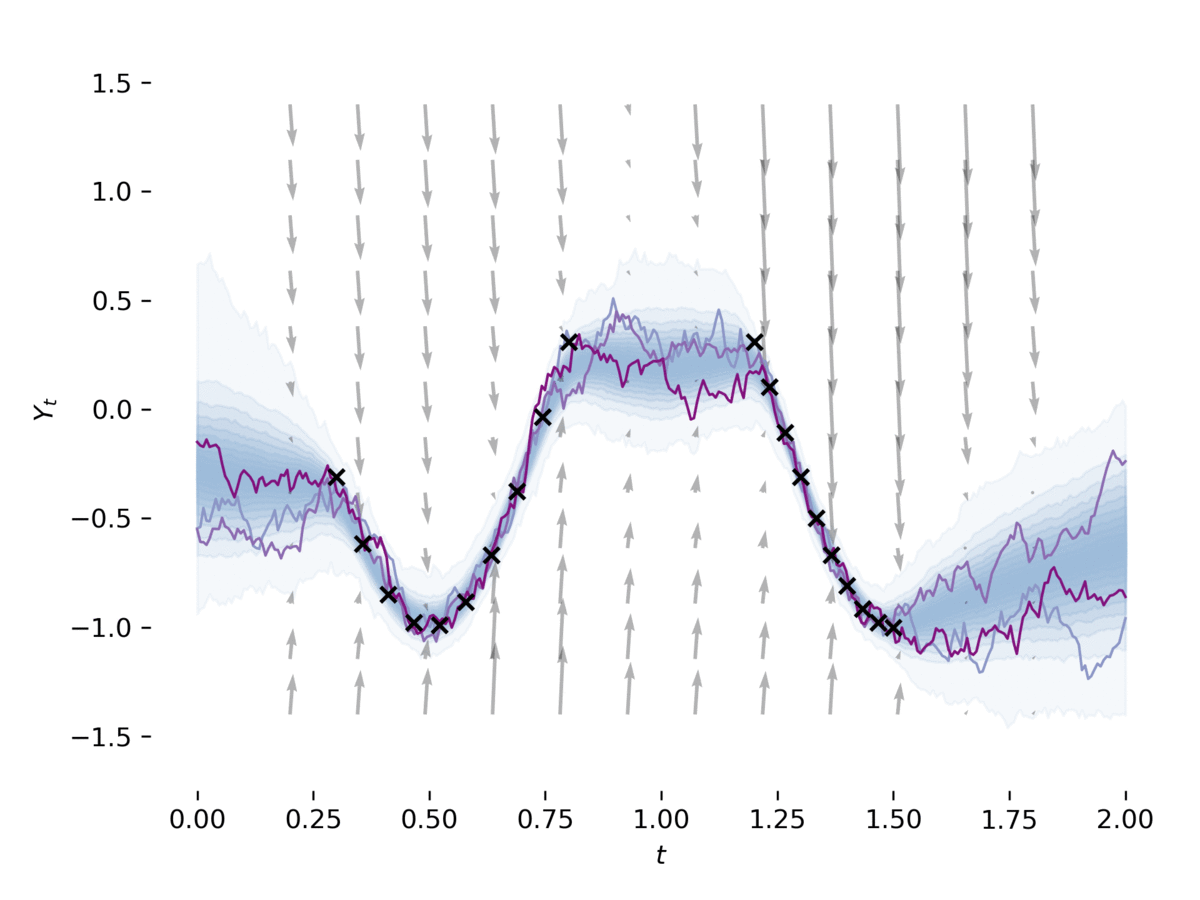
examples/sde_gan.py изучают SDE как Gan, как в [2], [3]. Пример обучает SDE в качестве генератора GAN, используя нейронную CDE [4] в качестве дискриминатора. Этот пример можно запустить через

python -m examples.sde_gan

Цитирование

Если вы нашли эту кодовую базу полезной в своем исследовании, пожалуйста, рассмотрите возможность сослаться на любое или оба:

 @article{li2020scalable,
  title={Scalable gradients for stochastic differential equations},
  author={Li, Xuechen and Wong, Ting-Kam Leonard and Chen, Ricky T. Q. and Duvenaud, David},
  journal={International Conference on Artificial Intelligence and Statistics},
  year={2020}
}

 @article{kidger2021neuralsde,
  title={Neural {SDE}s as {I}nfinite-{D}imensional {GAN}s},
  author={Kidger, Patrick and Foster, James and Li, Xuechen and Oberhauser, Harald and Lyons, Terry},
  journal={International Conference on Machine Learning},
  year={2021}
}

Ссылки

[1] Сюэхен Ли, Тинг-Кэм Леонард Вонг, Рики Т. К. Чен, Дэвид Дувена. «Масштабируемые градиенты для стохастических дифференциальных уравнений». Международная конференция по искусственному интеллекту и статистике. 2020. [arxiv]

[2] Патрик Киджер, Джеймс Фостер, Сюэхен Ли, Харальд Оберхаузер, Терри Лионс. «Нейронные SDE как бесконечномерные ганс». Международная конференция по машинному обучению 2021. [arxiv]

[3] Патрик Киджер, Джеймс Фостер, Сюэхен Ли, Терри Лайонс. «Эффективные и точные градиенты для нейронных SDE». 2021. [arxiv]

[4] Патрик Киджер, Джеймс Моррилл, Джеймс Фостер, Терри Лайонс, «Дифференциальные уравнения, контролируемые нейро, для нерегулярных временных рядов». Системы обработки нейронной информации 2020. [arxiv]

---

Это исследовательский проект, а не официальный продукт Google.