torchsde

Implementación de Pytorch de solucionadores SDE diferenciables

Esta biblioteca proporciona solucionadores de ecuación diferencial estocástica (SDE) con soporte de GPU y backpropagación eficiente.

---

Instalación

pip install torchsde

Requisitos: Python> = 3.8 y Pytorch> = 1.6.0.

Documentación

Disponible aquí.

Ejemplos

Ejemplo rápido

 import torch
import torchsde

batch_size , state_size , brownian_size = 32 , 3 , 2
t_size = 20

class SDE ( torch . nn . Module ):
    noise_type = 'general'
    sde_type = 'ito'

    def __init__ ( self ):
        super (). __init__ ()
        self . mu = torch . nn . Linear ( state_size , 
                                  state_size )
        self . sigma = torch . nn . Linear ( state_size , 
                                     state_size * brownian_size )

    # Drift
    def f ( self , t , y ):
        return self . mu ( y )  # shape (batch_size, state_size)

    # Diffusion
    def g ( self , t , y ):
        return self . sigma ( y ). view ( batch_size , 
                                  state_size , 
                                  brownian_size )

sde = SDE ()
y0 = torch . full (( batch_size , state_size ), 0.1 )
ts = torch . linspace ( 0 , 1 , t_size )
# Initial state y0, the SDE is solved over the interval [ts[0], ts[-1]].
# ys will have shape (t_size, batch_size, state_size)
ys = torchsde . sdeint ( sde , y0 , ts )

Computadora portátil

examples/demo.ipynb ofrece una breve guía sobre cómo resolver SDE, incluidos puntos sutiles como la fijación de la aleatoriedad en el solucionador y la elección de los tipos de ruido .

SDE latente

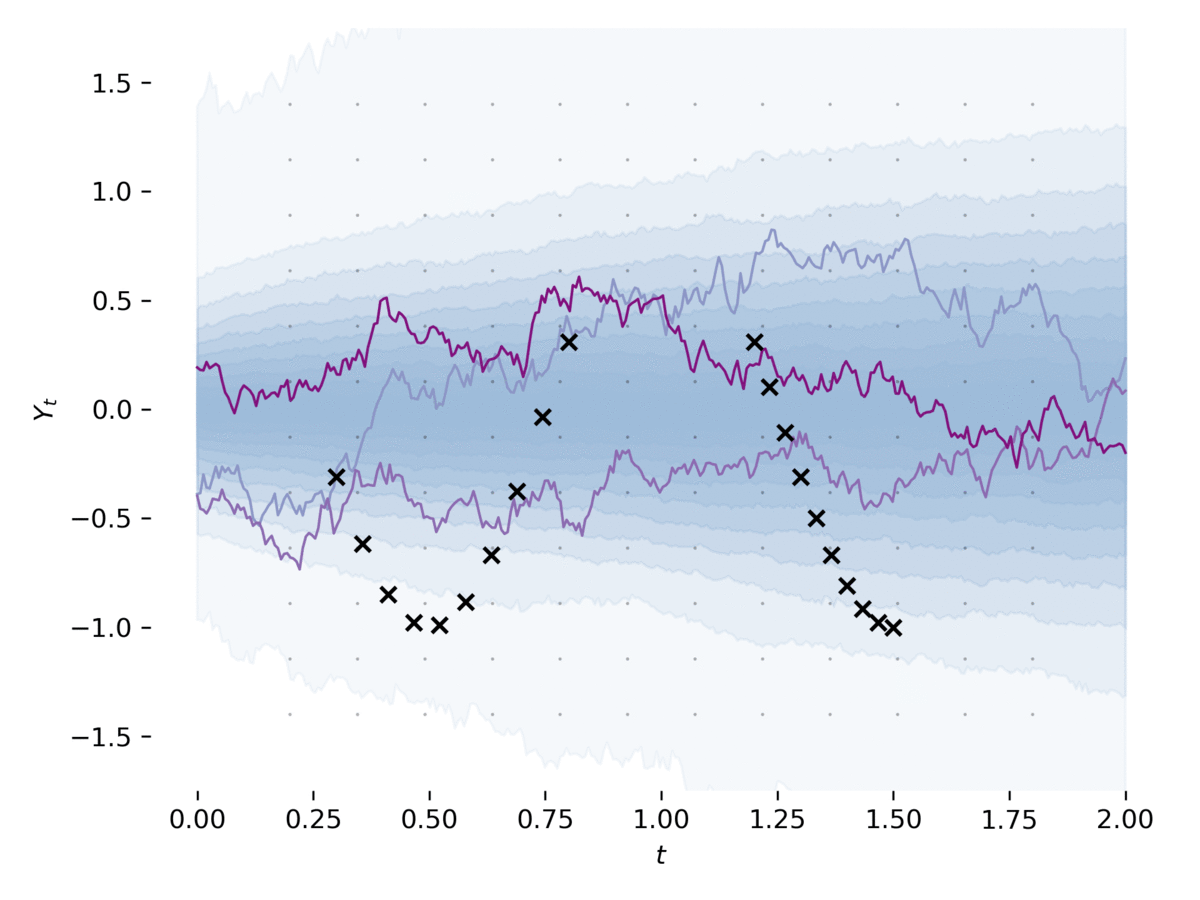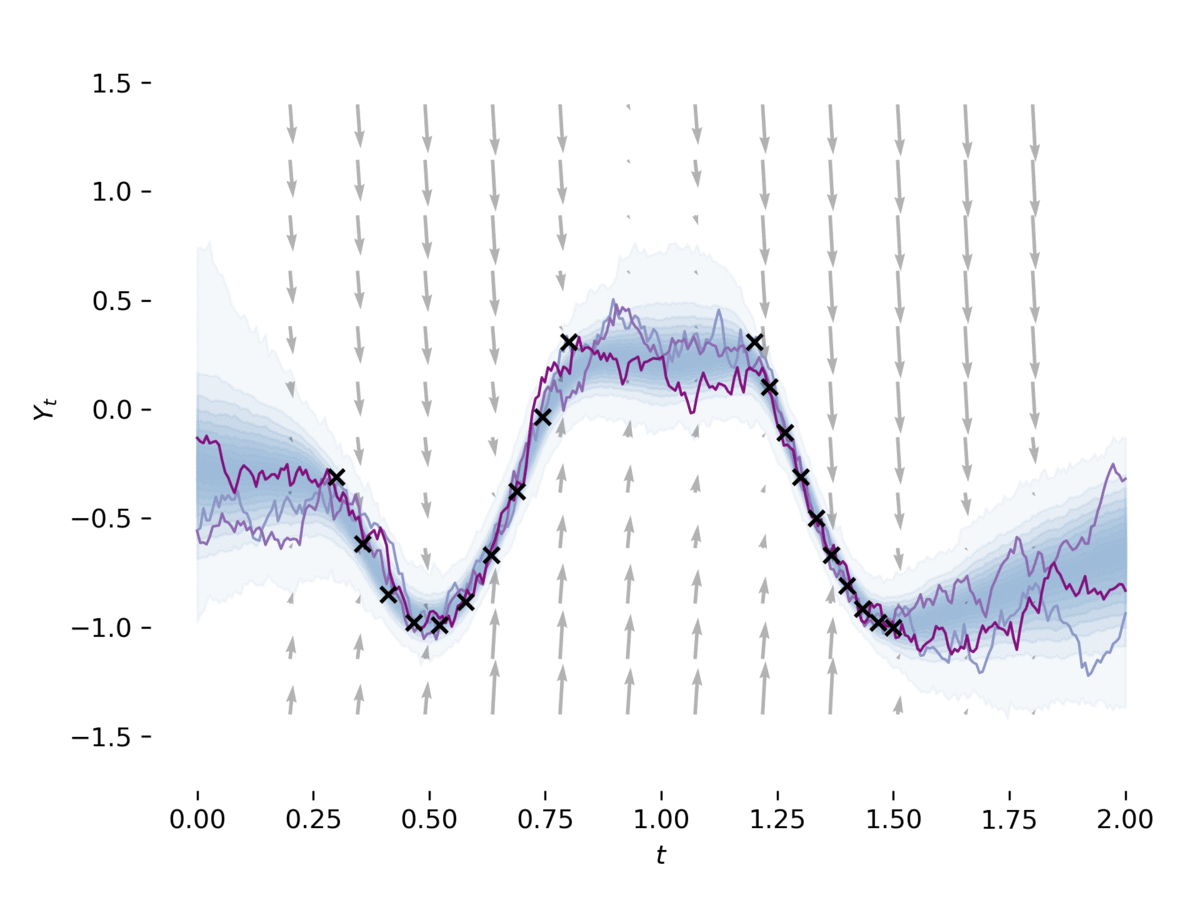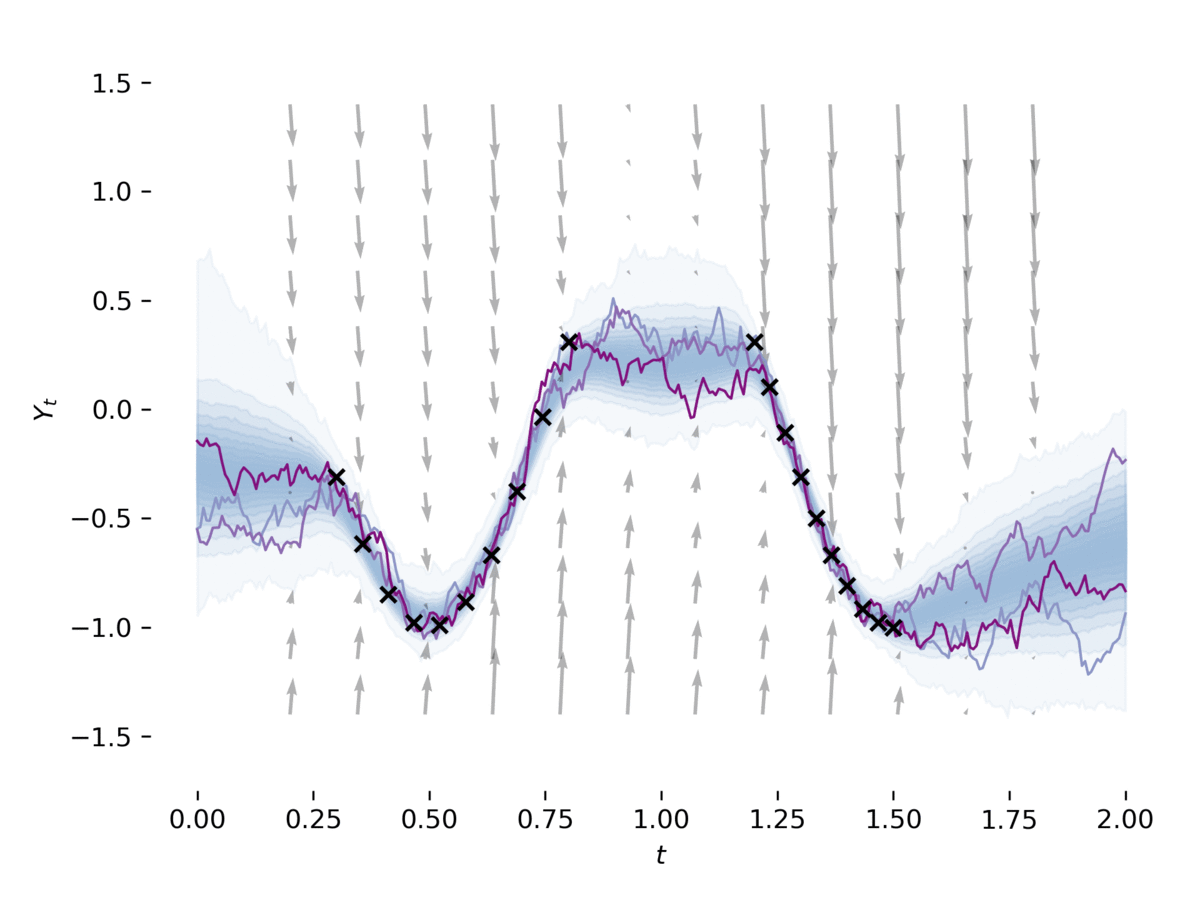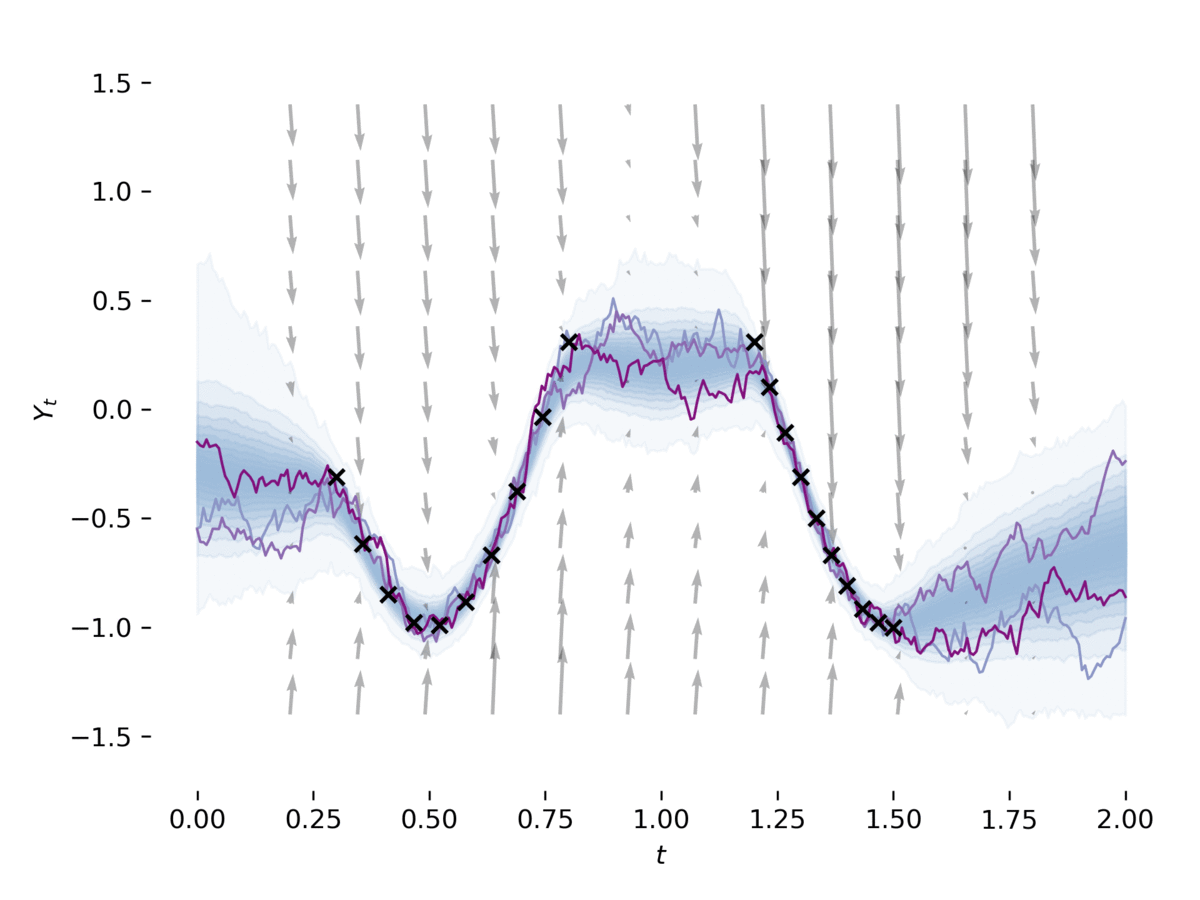
examples/latent_sde.py aprende una ecuación diferencial estocástica latente , como en la Sección 5 de [1]. El ejemplo se ajusta a un SDE a los datos, al tiempo que lo regulariza como un proceso previo de Ornstein-Uhlenbeck. El modelo puede verse libremente como un autoencoder variacional con su ser SDES posterior y aproximado. Este ejemplo se puede ejecutar a través de

python -m examples.latent_sde --train-dir < TRAIN_DIR >

El programa genera cifras a la ruta especificada por <TRAIN_DIR> . El entrenamiento debe estabilizarse después de 500 iteraciones con los hiperparámetros predeterminados.

SDE neural como Gans

examples/sde_gan.py aprende un SDE como GaN, como en [2], [3]. El ejemplo entrena un SDE como generador de un GaN, al tiempo que usa un CDE neural [4] como discriminador. Este ejemplo se puede ejecutar a través de

python -m examples.sde_gan

Citación

Si encontró esta base de código útil en su investigación, considere citar cualquiera o ambos de:

 @article{li2020scalable,
  title={Scalable gradients for stochastic differential equations},
  author={Li, Xuechen and Wong, Ting-Kam Leonard and Chen, Ricky T. Q. and Duvenaud, David},
  journal={International Conference on Artificial Intelligence and Statistics},
  year={2020}
}

 @article{kidger2021neuralsde,
  title={Neural {SDE}s as {I}nfinite-{D}imensional {GAN}s},
  author={Kidger, Patrick and Foster, James and Li, Xuechen and Oberhauser, Harald and Lyons, Terry},
  journal={International Conference on Machine Learning},
  year={2021}
}

Referencias

[1] Xuechen LI, Ting-Kam Leonard Wong, Ricky Tq Chen, David Duvenaud. "Gradientes escalables para ecuaciones diferenciales estocásticas". Conferencia internacional sobre inteligencia y estadísticas artificiales. 2020. [ARXIV]

[2] Patrick Kidger, James Foster, Xuechen LI, Harald Oberhauser, Terry Lyons. "SDE neural como Gans infinitas-dimensionales". Conferencia internacional sobre aprendizaje automático 2021. [ARXIV]

[3] Patrick Kidger, James Foster, Xuechen LI, Terry Lyons. "Gradientes eficientes y precisos para las SDE neurales". 2021. [ARXIV]

[4] Patrick Kidger, James Morrill, James Foster, Terry Lyons, "Ecuaciones diferenciales controladas neuronales para series de tiempo irregulares". Sistemas de procesamiento de información neural 2020. [ARXIV]

---

Este es un proyecto de investigación, no un producto oficial de Google.