pytorch_wavelets

2D小波在Pytorch中變換

完整的文檔也可以在此處提供。

該軟件包為計算2D離散小波和2D雙樹複合小波的變換，它們的對倒置以及通過Pytorch的傳遞梯度提供了支持。

該實現旨在與多通道圖像批量一起使用。我們使用具有“ NCHW”數據格式的標準Pytorch實現。

我們還添加了層以進行2-D DTCWT的散點網。這類似於Kymatio中Morlet的散點網，但大約要快10倍。

如果您使用此回購，請引用我的博士學位論文，第3章：https：//doi.org/10.17863/cam.53748。

新版本1.3.0

• 添加了1D DWT支持

 import torch
from pytorch_wavelets import DWT1DForward , DWT1DInverse  # or simply DWT1D, IDWT1D
dwt = DWT1DForward ( wave = 'db6' , J = 3 )
X = torch . randn ( 10 , 5 , 100 )
yl , yh = dwt ( X )
print ( yl . shape )
> >> torch . Size ([ 10 , 5 , 22 ])
print ( yh [ 0 ]. shape )
> >> torch . Size ([ 10 , 5 , 55 ])
print ( yh [ 1 ]. shape )
> >> torch . Size ([ 10 , 5 , 33 ])
print ( yh [ 2 ]. shape )
> >> torch . Size ([ 10 , 5 , 22 ])
idwt = DWT1DInverse ( wave = 'db6' )
x = idwt (( yl , yh ))

新版本1.2.0

• 添加了基於DTCWT的散點網

 import torch
from pytorch_wavelets import ScatLayer
scat = ScatLayer ()
X = torch . randn ( 10 , 5 , 64 , 64 )
# A first order scatternet with 6 orientations and one lowpass channels
# gives 7 times the input channel dimension
Z = scat ( X )
print ( Z . shape )
> >> torch . Size ([ 10 , 35 , 32 , 32 ])
# A second order scatternet with 6 orientations and one lowpass channels
# gives 7^2 times the input channel dimension
scat2 = torch . nn . Sequential ( ScatLayer (), ScatLayer ())
Z = scat2 ( X )
print ( Z . shape )
> >> torch . Size ([ 10 , 245 , 16 , 16 ])
# We also have a slightly more specialized, but slower, second order scatternet
from pytorch_wavelets import ScatLayerj2
scat2a = ScatLayerj2 ()
Z = scat2a ( X )
print ( Z . shape )
> >> torch . Size ([ 10 , 245 , 16 , 16 ])
# These all of course work with cuda
scat2a . cuda ()
Z = scat2a ( X . cuda ())

新版本1.1.0

• DWT的固定內存問題
• 修復了DTCWT計算的後端代碼 - 現在更清潔，但性能相似
• DTCWT和DWT現在都應該更有效/知道。
• 刪除需要指定dtcwtinverse的量表數量

新版本1.0.0

版本1.0.0現在添加了對可分離DWT計算的支持，以及更多的填充方案，例如對稱，零和分期。

同樣，在創建小波變換類時，不再需要指定通道數。

速度測試

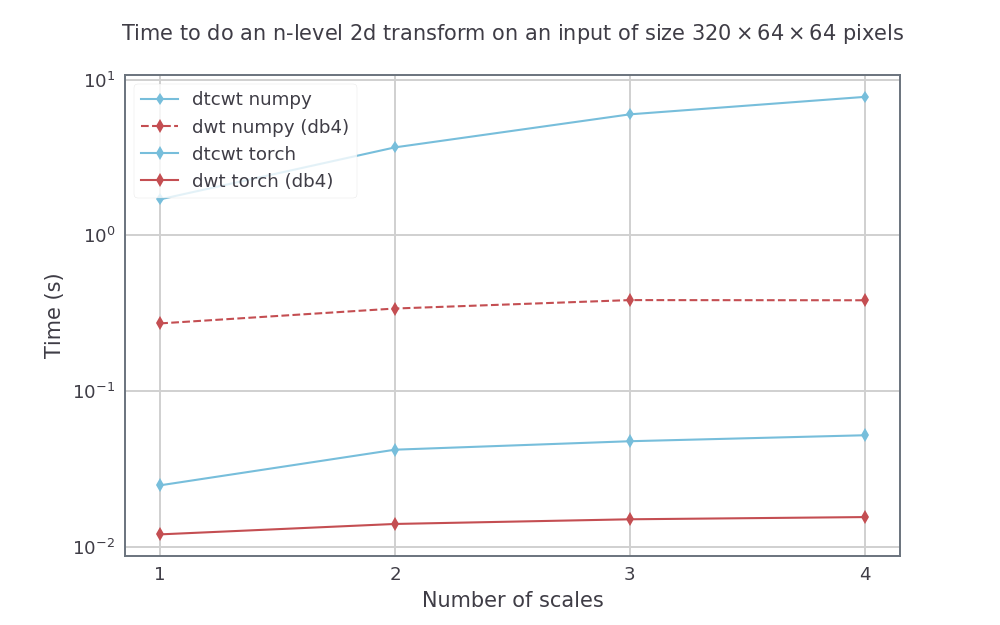
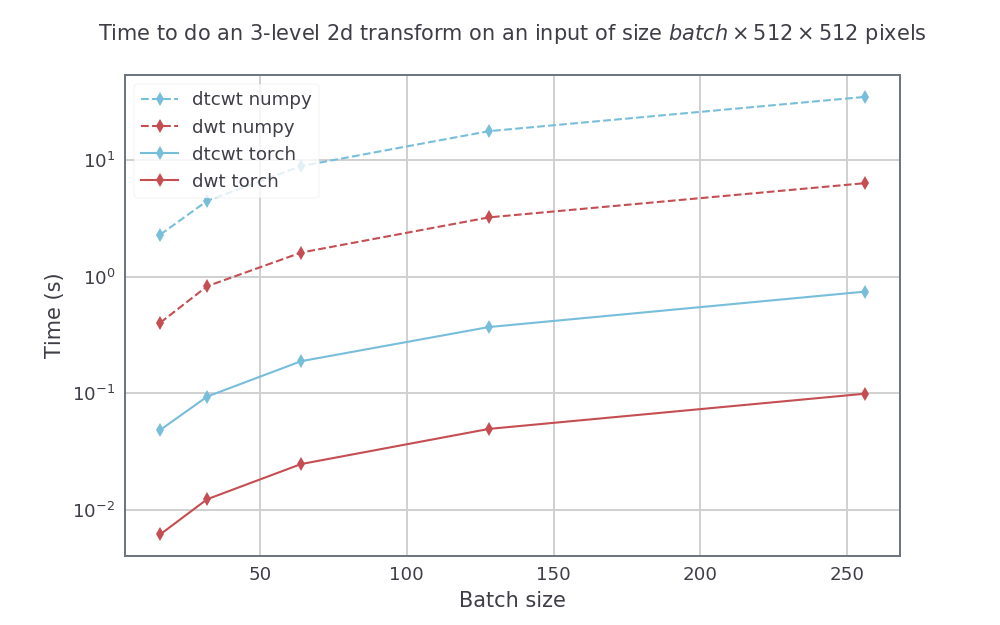
我們將DTCWT與Python包進行比較，並使用GTX1080在Pytorch_wavelets中進行DWT進行DWT進行比較。使用英特爾的平行python，在14核Xeon Phi機器上運行Numpy方法。對於DTWCWT，我們將近_sym_a濾波器用於第一刻度和QSHIFT_A濾波器以進行後續尺度。對於DWT，我們使用DB4過濾器。

對於固定的輸入尺寸，但是改變了尺度的數量（從1到4），我們的速度（平均為5個運行）：

對於具有高度和寬度512 x 512的輸入尺寸，我們還可以改變3刻度轉換的批次大小。由此產生的速度是：

安裝

安裝pytorch_wavelets的最簡單方法是克隆回購併安裝PIP。以後的版本將在PYPI上發布，但文檔需要首先更新：

 $ git克隆https://github.com/fbcotter/pytorch_wavelets
$ cd pytorch_wavelets
$ pip安裝。

（儘管如果您打算對庫進行任何重大修改，則開發命令可能會更有用。）提供了測試套件，以便您可以驗證系統上的代碼工作：

 $ pip install -r tests/supports.txt
$ PYTEST測試/

示例使用

對於DWT-請注意，高通輸出具有額外的尺寸，其中我們將（LH，HL，HH）係數堆疊起來。另請注意，YH輸出首先具有最好的細節係數，而最粗糙的係數則是最高的（與Pywavelets相反）。

 import torch
from pytorch_wavelets import DWTForward , DWTInverse
xfm = DWTForward ( J = 3 , wave = 'db3' , mode = 'zero' )
X = torch . randn ( 10 , 5 , 64 , 64 )
Yl , Yh = xfm ( X )
print ( Yl . shape )
> >> torch . Size ([ 10 , 5 , 12 , 12 ])
print ( Yh [ 0 ]. shape )
> >> torch . Size ([ 10 , 5 , 3 , 34 , 34 ])
print ( Yh [ 1 ]. shape )
> >> torch . Size ([ 10 , 5 , 3 , 19 , 19 ])
print ( Yh [ 2 ]. shape )
> >> torch . Size ([ 10 , 5 , 3 , 12 , 12 ])
ifm = DWTInverse ( wave = 'db3' , mode = 'zero' )
Y = ifm (( Yl , Yh ))

對於DTCWT：

 import torch
from pytorch_wavelets import DTCWTForward , DTCWTInverse
xfm = DTCWTForward ( J = 3 , biort = 'near_sym_b' , qshift = 'qshift_b' )
X = torch . randn ( 10 , 5 , 64 , 64 )
Yl , Yh = xfm ( X )
print ( Yl . shape )
> >> torch . Size ([ 10 , 5 , 16 , 16 ])
print ( Yh [ 0 ]. shape )
> >> torch . Size ([ 10 , 5 , 6 , 32 , 32 , 2 ])
print ( Yh [ 1 ]. shape )
> >> torch . Size ([ 10 , 5 , 6 , 16 , 16 , 2 ])
print ( Yh [ 2 ]. shape )
> >> torch . Size ([ 10 , 5 , 6 , 8 , 8 , 2 ])
ifm = DTCWTInverse ( biort = 'near_sym_b' , qshift = 'qshift_b' )
Y = ifm (( Yl , Yh ))

一些初始註釋：

• YH回來的是一個元組。有兩個額外的維度 - 第一個尺寸是在輸入的通道維度和行維數之間。這是DTCWT的6個方向。第二個是最終維度，它是真實的零件（副本不是Pytorch的本地）

在GPU上運行

對於Pytorch用戶來說，這不足為奇。 DWT和DTCWT轉換支持CUDA調用：

 import torch
from pytorch_wavelets import DTCWTForward , DTCWTInverse
xfm = DTCWTForward ( J = 3 , biort = 'near_sym_b' , qshift = 'qshift_b' ). cuda ()
X = torch . randn ( 10 , 5 , 64 , 64 ). cuda ()
Yl , Yh = xfm ( X )
ifm = DTCWTInverse ( biort = 'near_sym_b' , qshift = 'qshift_b' ). cuda ()
Y = ifm (( Yl , Yh ))

自動測試無法測試GPU功能，但請檢查CPU運行。要測試存儲庫是否正在處理您的GPU，您可以下載倉庫，確保您使用啟用CUDA的Pytorch（測試將檢查torch.cuda.is_available()是否返回true），然後運行：

 PIP安裝-R測試/需求.txt
pytest測試/

從存儲庫的底部。

反向傳播

可以將梯度通過前向和向後變換。您需要做的就是確保每個對每個的輸入設置為true。

出處

基於劍橋大學尼克·金斯伯里（Nick Kingsbury）的MATLAB的雙樹複雜小波變換包。可以在Original_readme.txt中找到原始讀數。該文件概述了原始MATLAB工具箱的使用條件。

有關DT CWT的更多信息，可以從可從我的網站下載的論文獲得（下面給出）。最好的教程是在1999年的皇家學會論文中。特別是這解釋了“真實”四肢 - 數字子圖像與復雜子圖的對之間的轉換。 Q-Shift過濾器在ICIP 2000論文中進行了解釋，並在2001年5月的《應用和計算諧波分析》雜誌的《 2001年5月論文》中進行了詳細說明。

該代碼是版權，僅用於研究目的免費提供。作為提供代碼的回報，我要問的是，如果您使用算法，則在您撰寫的任何論文中給出了適當的參考，並讓我知道是否找到了DT CWT的任何好應用。如果應用程序很好，我將對協作非常感興趣。我不接受使用這些算法而產生的責任。

尼克·金斯伯里（Nick Kingsbury），劍橋大學，2003年6月。

劍橋大學，特朗普頓街，英國劍橋CB2 1pz。電話：（0或+44）1223 338514 /332647;主頁：1954 211152;傳真：1223 338564 /332662;電子郵件：[email protected]網絡主頁：http：//www.eng.cam.ac.uk/~ngk/