Полная документация также доступна здесь.
Этот пакет обеспечивает поддержку для вычисления двухмерного дискретного вейвлета и двухмерного вейвлет-преобразований, их обращений и прохождения градиентов 2D с двумя деревьями.
Реализация предназначена для использования с партиями многоканальных изображений. Мы используем стандартную реализацию Pytorch с помощью формата данных NCHW.
Мы также добавили слои для выполнения 2-D DTCWT Scatternet. Это похоже на разброс на основе Morlet в Kymatio, но примерно в 10 раз быстрее.
Если вы используете это репо, пожалуйста, укажите мою диссертация доктора философии, глава 3: https://doi.org/10.17863/cam.53748.
import torch
from pytorch_wavelets import DWT1DForward , DWT1DInverse # or simply DWT1D, IDWT1D
dwt = DWT1DForward ( wave = 'db6' , J = 3 )
X = torch . randn ( 10 , 5 , 100 )
yl , yh = dwt ( X )
print ( yl . shape )
> >> torch . Size ([ 10 , 5 , 22 ])
print ( yh [ 0 ]. shape )
> >> torch . Size ([ 10 , 5 , 55 ])
print ( yh [ 1 ]. shape )
> >> torch . Size ([ 10 , 5 , 33 ])
print ( yh [ 2 ]. shape )
> >> torch . Size ([ 10 , 5 , 22 ])
idwt = DWT1DInverse ( wave = 'db6' )
x = idwt (( yl , yh )) import torch
from pytorch_wavelets import ScatLayer
scat = ScatLayer ()
X = torch . randn ( 10 , 5 , 64 , 64 )
# A first order scatternet with 6 orientations and one lowpass channels
# gives 7 times the input channel dimension
Z = scat ( X )
print ( Z . shape )
> >> torch . Size ([ 10 , 35 , 32 , 32 ])
# A second order scatternet with 6 orientations and one lowpass channels
# gives 7^2 times the input channel dimension
scat2 = torch . nn . Sequential ( ScatLayer (), ScatLayer ())
Z = scat2 ( X )
print ( Z . shape )
> >> torch . Size ([ 10 , 245 , 16 , 16 ])
# We also have a slightly more specialized, but slower, second order scatternet
from pytorch_wavelets import ScatLayerj2
scat2a = ScatLayerj2 ()
Z = scat2a ( X )
print ( Z . shape )
> >> torch . Size ([ 10 , 245 , 16 , 16 ])
# These all of course work with cuda
scat2a . cuda ()
Z = scat2a ( X . cuda ())Версия 1.0.0 теперь добавила поддержку для разделяемого расчета DWT и больше схем накладки, таких как симметричная, ноль и периодизация.
Кроме того, больше не нужно указывать количество каналов при создании классов вейвлет -преобразований.
Мы сравниваем выполнение DTCWT с пакетом Python и выполняем DWT с PyWaveLets, чтобы выполнять оба в Pytorch_Waelets, используя GTX1080. Методы Numpy были запущены на 14 -яйер -PHI -машине с использованием параллельного Python Intel. Для DTWCWT мы используем фильтры ROLE_SYM_A для первой шкалы и фильтры QSHIFT_A для последующих масштабов. Для DWT мы используем фильтры DB4.
Для фиксированного размера входа, но изменяя количество шкал (от 1 до 4), у нас есть следующие скорости (в среднем по 5 прогонов):
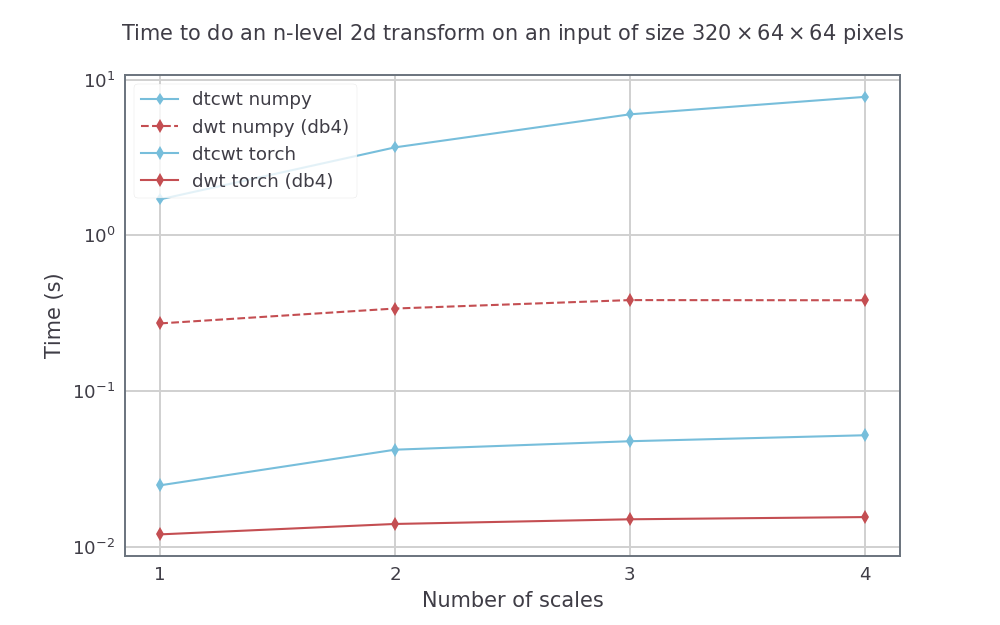
Для входного размера с высотой и шириной 512 на 512 мы также изменяем размер партии для 3 -х масштабного преобразования. Полученными скоростями были:
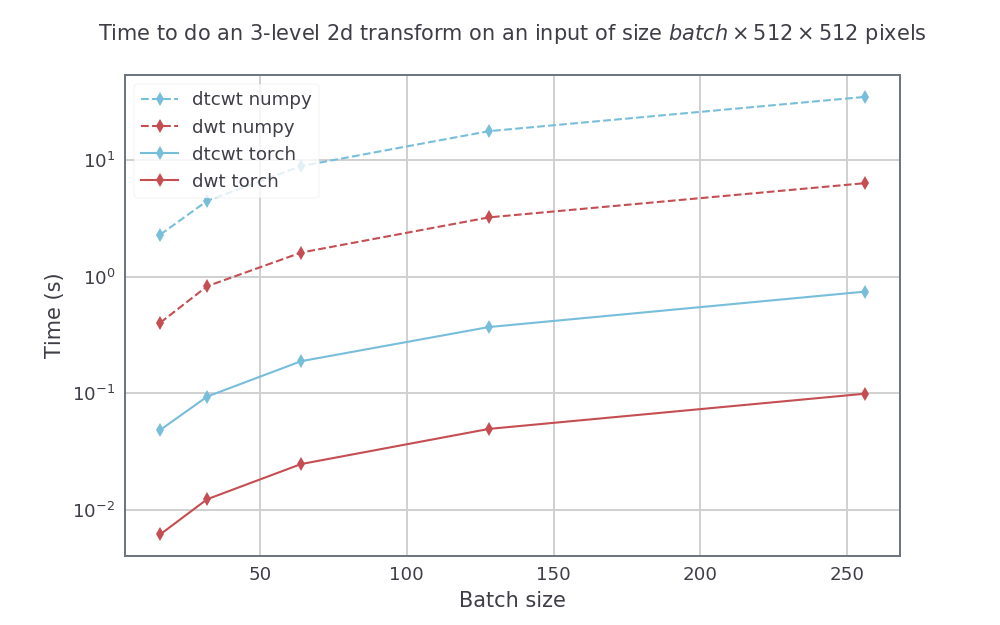
Самый простой способ установить pytorch_wavelets - клонировать репо и PIP установить его. Более поздние версии будут выпущены на PYPI, но документы должны сначала обновить:
$ git clone https://github.com/fbcotter/pytorch_waelets $ cd pytorch_waelets $ pip установка.
(Хотя команда разработки может быть более полезной, если вы намереваетесь выполнить какую -либо существенную модификацию библиотеки.) Предоставлен тестовый набор, чтобы вы могли проверить, что код работает в вашей системе:
$ pip install -r tests/tests.txt $ pytest тесты/
Для DWT - обратите внимание, что выходной выход имеет дополнительное измерение, в котором мы складываем коэффициенты (LH, HL, HH). Также обратите внимание, что вывод YH в первую очередь имеет лучшие коэффициенты детализации, а самый грубый последний (противоположный Pywavelets).
import torch
from pytorch_wavelets import DWTForward , DWTInverse
xfm = DWTForward ( J = 3 , wave = 'db3' , mode = 'zero' )
X = torch . randn ( 10 , 5 , 64 , 64 )
Yl , Yh = xfm ( X )
print ( Yl . shape )
> >> torch . Size ([ 10 , 5 , 12 , 12 ])
print ( Yh [ 0 ]. shape )
> >> torch . Size ([ 10 , 5 , 3 , 34 , 34 ])
print ( Yh [ 1 ]. shape )
> >> torch . Size ([ 10 , 5 , 3 , 19 , 19 ])
print ( Yh [ 2 ]. shape )
> >> torch . Size ([ 10 , 5 , 3 , 12 , 12 ])
ifm = DWTInverse ( wave = 'db3' , mode = 'zero' )
Y = ifm (( Yl , Yh ))Для DTCWT:
import torch
from pytorch_wavelets import DTCWTForward , DTCWTInverse
xfm = DTCWTForward ( J = 3 , biort = 'near_sym_b' , qshift = 'qshift_b' )
X = torch . randn ( 10 , 5 , 64 , 64 )
Yl , Yh = xfm ( X )
print ( Yl . shape )
> >> torch . Size ([ 10 , 5 , 16 , 16 ])
print ( Yh [ 0 ]. shape )
> >> torch . Size ([ 10 , 5 , 6 , 32 , 32 , 2 ])
print ( Yh [ 1 ]. shape )
> >> torch . Size ([ 10 , 5 , 6 , 16 , 16 , 2 ])
print ( Yh [ 2 ]. shape )
> >> torch . Size ([ 10 , 5 , 6 , 8 , 8 , 2 ])
ifm = DTCWTInverse ( biort = 'near_sym_b' , qshift = 'qshift_b' )
Y = ifm (( Yl , Yh ))Некоторые первоначальные примечания:
Это не должно быть удивлением для пользователей Pytorch. DWT и DTCWT преобразует поддержку CUDA Calling:
import torch
from pytorch_wavelets import DTCWTForward , DTCWTInverse
xfm = DTCWTForward ( J = 3 , biort = 'near_sym_b' , qshift = 'qshift_b' ). cuda ()
X = torch . randn ( 10 , 5 , 64 , 64 ). cuda ()
Yl , Yh = xfm ( X )
ifm = DTCWTInverse ( biort = 'near_sym_b' , qshift = 'qshift_b' ). cuda ()
Y = ifm (( Yl , Yh )) Автоматизированные тесты не могут проверить функциональность GPU, но проверяйте запуск процессора. Чтобы проверить, работает ли репо над вашим GPU, вы можете загрузить репо, убедиться, что у вас есть Pytorch с включенной CUDA (тесты будут проверять, чтобы увидеть, возвращает ли torch.cuda.is_available() и запустить:
PIP установка -R -тесты/требования. Pytest тесты/
От основания репо.
Можно пройти градиенты через передовые и обратные преобразования. Все, что вам нужно сделать, это убедиться, что ввод для каждого из них имеет необходимый атрибут_ГРИИ, установленную в TRUE.
Основанный на пакете вейвлет-преобразования комплекса с двойным деревом для Matlab от Ника Кингсбери, Кембриджский университет. Оригинальный Readme можно найти в original_readme.txt. В этом файле изложены условия использования исходного набора инструментов MATLAB.
Дополнительную информацию о DT CWT можно получить из документов, загружаемых с моего веб -сайта (приведено ниже). Лучший учебник - в документе Королевского общества 1999 года. В частности, это объясняет преобразование между «реальными» четырехмельными сумматорами и парами сложных субмиджиров. Фильтры Q-сдвига объясняются в статье ICIP 2000 и более подробно в статье в мае 2001 года для журнала по применению и вычислительной гармонической анализе.
Этот код является авторским правом и предоставляется бесплатно только для исследовательских целей. В обмен на поставку кода, все, что я спрашиваю, это то, что, если вы используете алгоритмы, вы указываете на эту работу в любых документах, которые вы пишете, и что вы дали мне знать, если вы найдете какие -либо хорошие приложения для DT CWT. Если приложения хороши, я был бы очень заинтересован в сотрудничестве. Я не принимаю ответственности, возникающей в результате использования этих алгоритмов.
Ник Кингсбери, Кембриджский университет, июнь 2003 г.
Доктор Нг Кингсбери, кафедра инженерии, Университет Кембриджа, ул. Трампингтон, Кембридж CB2 1PZ, Великобритания, или Тринити -колледж, Кембридж CB2 1TQ, Великобритания. Телефон: (0 или +44) 1223 338514 /332647; Главная: 1954 211152; Факс: 1223 338564 /332662; Электронная почта: [email protected] Веб-домашняя страница: http://www.eng.cam.ac.uk/~ngk/