A documentação completa também está disponível aqui.
Este pacote fornece suporte para calcular a wavelet discreta 2D e as transformações de wavelet de dupla árvore 2D, seus inversos e passes de gradientes através de ambos usando pytorch.
A implementação foi projetada para ser usada com lotes de imagens multicanais. Utilizamos a implementação padrão do Pytorch de ter formato de dados 'NCHW'.
Também adicionamos camadas para fazer o ScatterNet baseado em DTCWT 2-D. Isso é semelhante ao ScatterNet baseado em Morlet em Kymatio, mas é aproximadamente 10 vezes mais rápido.
Se você usar este repositório, cite minha tese de doutorado, capítulo 3: https://doi.org/10.17863/cam.53748.
import torch
from pytorch_wavelets import DWT1DForward , DWT1DInverse # or simply DWT1D, IDWT1D
dwt = DWT1DForward ( wave = 'db6' , J = 3 )
X = torch . randn ( 10 , 5 , 100 )
yl , yh = dwt ( X )
print ( yl . shape )
> >> torch . Size ([ 10 , 5 , 22 ])
print ( yh [ 0 ]. shape )
> >> torch . Size ([ 10 , 5 , 55 ])
print ( yh [ 1 ]. shape )
> >> torch . Size ([ 10 , 5 , 33 ])
print ( yh [ 2 ]. shape )
> >> torch . Size ([ 10 , 5 , 22 ])
idwt = DWT1DInverse ( wave = 'db6' )
x = idwt (( yl , yh )) import torch
from pytorch_wavelets import ScatLayer
scat = ScatLayer ()
X = torch . randn ( 10 , 5 , 64 , 64 )
# A first order scatternet with 6 orientations and one lowpass channels
# gives 7 times the input channel dimension
Z = scat ( X )
print ( Z . shape )
> >> torch . Size ([ 10 , 35 , 32 , 32 ])
# A second order scatternet with 6 orientations and one lowpass channels
# gives 7^2 times the input channel dimension
scat2 = torch . nn . Sequential ( ScatLayer (), ScatLayer ())
Z = scat2 ( X )
print ( Z . shape )
> >> torch . Size ([ 10 , 245 , 16 , 16 ])
# We also have a slightly more specialized, but slower, second order scatternet
from pytorch_wavelets import ScatLayerj2
scat2a = ScatLayerj2 ()
Z = scat2a ( X )
print ( Z . shape )
> >> torch . Size ([ 10 , 245 , 16 , 16 ])
# These all of course work with cuda
scat2a . cuda ()
Z = scat2a ( X . cuda ())A versão 1.0.0 agora adicionou suporte para cálculo DWT separável e mais esquemas de preenchimento, como simétrico, zero e periodização.
Além disso, não precisa mais especificar o número de canais ao criar as classes de transformação wavelet.
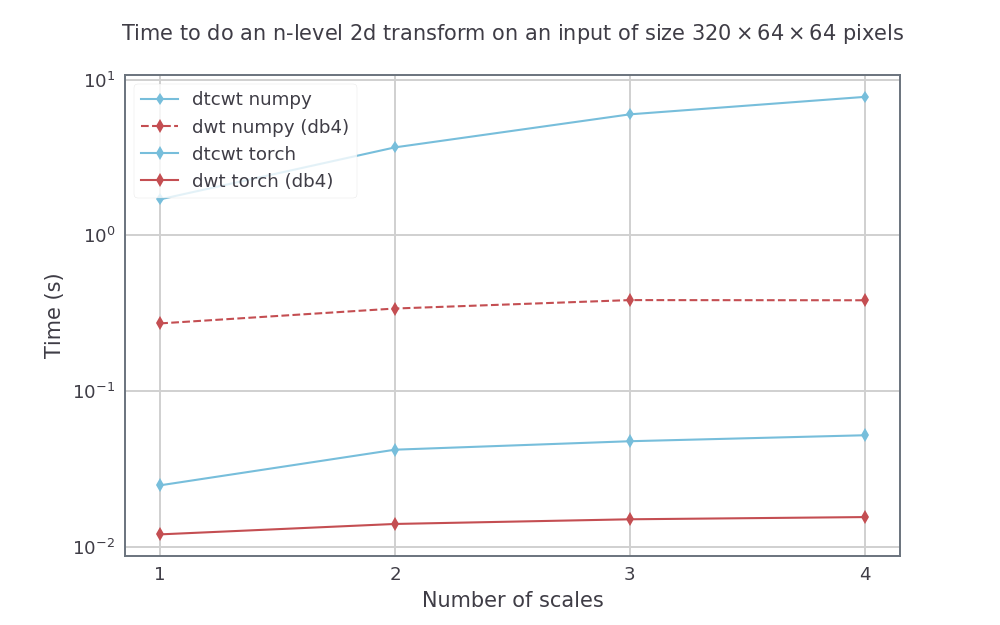
Comparamos fazer o DTCWT com o pacote Python e fazer o DWT com as owavelets para fazer os dois em pytorch_wavelets, usando um GTX1080. Os métodos Numpy foram executados em uma máquina Xeon Phi de 14 núcleo usando o Python paralelo da Intel. Para o DTWCWT, usamos os filtros NOST_SYM_A para a primeira escala e os filtros Qshift_A para escalas subsequentes. Para o DWT, usamos os filtros DB4.
Para um tamanho de entrada fixo, mas variando o número de escalas (de 1 a 4), temos as seguintes velocidades (média de 5 execuções):
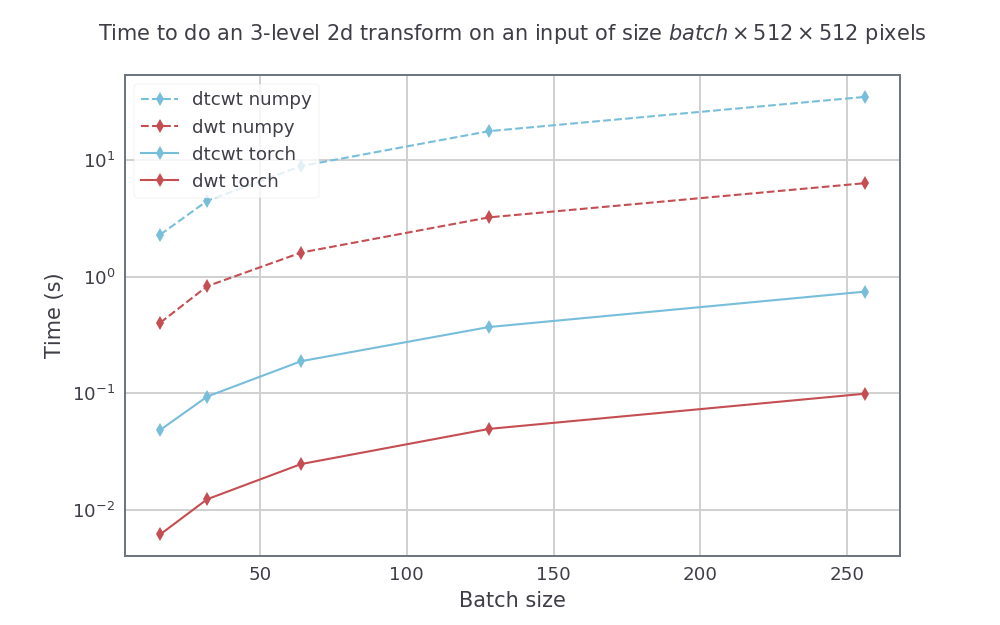
Para um tamanho de entrada com altura e largura 512 por 512, também variamos o tamanho do lote para uma transformação de 3 escalas. As velocidades resultantes foram:
A maneira mais fácil de instalar pytorch_wavelets é clonar o repo e instalá -lo. As versões posteriores serão lançadas no Pypi, mas os documentos precisam ser atualizados primeiro:
$ git clone https://github.com/fbcotter/pytorch_wavelets $ CD pytorch_wavelets $ pip install.
(Embora o comando de desenvolvimento possa ser mais útil se você pretende executar qualquer modificação significativa na biblioteca.) É fornecido um conjunto de testes para que você possa verificar se o código funciona no seu sistema:
$ pip install -r tests/requisitos.txt $ pytest testes/
Para o DWT - Observe que a saída do HighPass tem uma dimensão extra, na qual empilhamos os coeficientes (LH, HL, HH). Observe também que a saída YH possui os melhores coeficientes de detalhes primeiro e o último mais grosseiro (o oposto das ondas de pywavelets).
import torch
from pytorch_wavelets import DWTForward , DWTInverse
xfm = DWTForward ( J = 3 , wave = 'db3' , mode = 'zero' )
X = torch . randn ( 10 , 5 , 64 , 64 )
Yl , Yh = xfm ( X )
print ( Yl . shape )
> >> torch . Size ([ 10 , 5 , 12 , 12 ])
print ( Yh [ 0 ]. shape )
> >> torch . Size ([ 10 , 5 , 3 , 34 , 34 ])
print ( Yh [ 1 ]. shape )
> >> torch . Size ([ 10 , 5 , 3 , 19 , 19 ])
print ( Yh [ 2 ]. shape )
> >> torch . Size ([ 10 , 5 , 3 , 12 , 12 ])
ifm = DWTInverse ( wave = 'db3' , mode = 'zero' )
Y = ifm (( Yl , Yh ))Para o dtcwt:
import torch
from pytorch_wavelets import DTCWTForward , DTCWTInverse
xfm = DTCWTForward ( J = 3 , biort = 'near_sym_b' , qshift = 'qshift_b' )
X = torch . randn ( 10 , 5 , 64 , 64 )
Yl , Yh = xfm ( X )
print ( Yl . shape )
> >> torch . Size ([ 10 , 5 , 16 , 16 ])
print ( Yh [ 0 ]. shape )
> >> torch . Size ([ 10 , 5 , 6 , 32 , 32 , 2 ])
print ( Yh [ 1 ]. shape )
> >> torch . Size ([ 10 , 5 , 6 , 16 , 16 , 2 ])
print ( Yh [ 2 ]. shape )
> >> torch . Size ([ 10 , 5 , 6 , 8 , 8 , 2 ])
ifm = DTCWTInverse ( biort = 'near_sym_b' , qshift = 'qshift_b' )
Y = ifm (( Yl , Yh ))Algumas notas iniciais:
Isso não deve surpreender os usuários do Pytorch. O DWT e o DTCWT Transforms suportam o CUDA Calling:
import torch
from pytorch_wavelets import DTCWTForward , DTCWTInverse
xfm = DTCWTForward ( J = 3 , biort = 'near_sym_b' , qshift = 'qshift_b' ). cuda ()
X = torch . randn ( 10 , 5 , 64 , 64 ). cuda ()
Yl , Yh = xfm ( X )
ifm = DTCWTInverse ( biort = 'near_sym_b' , qshift = 'qshift_b' ). cuda ()
Y = ifm (( Yl , Yh )) Os testes automatizados não podem testar a funcionalidade da GPU, mas verifique a CPU em execução. Para testar se o repositório está trabalhando na sua GPU, você pode fazer o download do repositório, verifique se possui pytorch com CUDA ativado (os testes verificarão se torch.cuda.is_available() retorna true) e executar:
pip install -r tests/requisitos.txt testes de pytest/
Da base do repo.
É possível passar gradientes pelas transformações para frente e para trás. Tudo o que você precisa fazer é garantir que a entrada para cada um tenha o atributo necessário_ grad definido como true.
Baseado no pacote de transformação de wavelet complexo de dupla árvore para Matlab por Nick Kingsbury, Universidade de Cambridge. O ReadMe original pode ser encontrado no original_readme.txt. Este arquivo descreve as condições de uso da caixa de ferramentas MATLAB original.
Informações adicionais sobre o DT CWT podem ser obtidas dos artigos para download do meu site (fornecido abaixo). O melhor tutorial é no artigo da Royal Society de 1999. Em particular, isso explica a conversão entre subimagens de número quádro 'real' e pares de subimagens complexas. Os filtros de Q-Shift são explicados no artigo ICIP 2000 e em mais detalhes no artigo de maio de 2001 para a revista em análise harmônica aplicada e computacional.
Este código é de direitos autorais e é fornecido gratuitamente apenas para fins de pesquisa. Em troca do fornecimento do código, tudo o que peço é que, se você usar os algoritmos, você concede referência a este trabalho em qualquer documento que escreva e que me avise se encontrar bons aplicativos para o DT CWT. Se os aplicativos forem bons, eu ficaria muito interessado em colaboração. Não aceito nenhuma responsabilidade decorrente do uso desses algoritmos.
Nick Kingsbury, Universidade de Cambridge, junho de 2003.
Dr. Ng Kingsbury, Departamento de Engenharia, Universidade de Cambridge, Trumpington St., Cambridge CB2 1PZ, Reino Unido, ou Trinity College, Cambridge CB2 1TQ, Reino Unido. Telefone: (0 ou +44) 1223 338514 /332647; Home: 1954 211152; Fax: 1223 338564 /332662; E-mail: [email protected] Página inicial da web: http://www.eng.cam.ac.uk/~ngk/