La documentation complète est également disponible ici.
Ce package prend en charge le calcul de l'ondelette discret 2D et des transformations en ondelettes complexes à double arbre 2D, de leurs inverses et des gradients qui passent par les deux à l'aide de pytorch.
L'implémentation est conçue pour être utilisée avec des lots d'images multicanaux. Nous utilisons la mise en œuvre standard Pytorch du format de données «NCHW».
Nous avons également ajouté des couches pour faire le dispersnet basé sur DTCWT 2-D. Ceci est similaire au Scatternet à base de morlette dans Kymatio, mais est environ 10 fois plus rapide.
Si vous utilisez ce dépôt, veuillez citer ma thèse de doctorat, chapitre 3: https://doi.org/10.17863/cam.53748.
import torch
from pytorch_wavelets import DWT1DForward , DWT1DInverse # or simply DWT1D, IDWT1D
dwt = DWT1DForward ( wave = 'db6' , J = 3 )
X = torch . randn ( 10 , 5 , 100 )
yl , yh = dwt ( X )
print ( yl . shape )
> >> torch . Size ([ 10 , 5 , 22 ])
print ( yh [ 0 ]. shape )
> >> torch . Size ([ 10 , 5 , 55 ])
print ( yh [ 1 ]. shape )
> >> torch . Size ([ 10 , 5 , 33 ])
print ( yh [ 2 ]. shape )
> >> torch . Size ([ 10 , 5 , 22 ])
idwt = DWT1DInverse ( wave = 'db6' )
x = idwt (( yl , yh )) import torch
from pytorch_wavelets import ScatLayer
scat = ScatLayer ()
X = torch . randn ( 10 , 5 , 64 , 64 )
# A first order scatternet with 6 orientations and one lowpass channels
# gives 7 times the input channel dimension
Z = scat ( X )
print ( Z . shape )
> >> torch . Size ([ 10 , 35 , 32 , 32 ])
# A second order scatternet with 6 orientations and one lowpass channels
# gives 7^2 times the input channel dimension
scat2 = torch . nn . Sequential ( ScatLayer (), ScatLayer ())
Z = scat2 ( X )
print ( Z . shape )
> >> torch . Size ([ 10 , 245 , 16 , 16 ])
# We also have a slightly more specialized, but slower, second order scatternet
from pytorch_wavelets import ScatLayerj2
scat2a = ScatLayerj2 ()
Z = scat2a ( X )
print ( Z . shape )
> >> torch . Size ([ 10 , 245 , 16 , 16 ])
# These all of course work with cuda
scat2a . cuda ()
Z = scat2a ( X . cuda ())La version 1.0.0 a maintenant ajouté une prise en charge du calcul DWT séparable, et plus de schémas de rembourrage, tels que symétrique, zéro et périodisation.
De plus, il n'est plus besoin de spécifier le nombre de canaux lors de la création des classes de transformation en ondelettes.
Nous comparons en faisant le DTCWT avec le package Python et en faisant le DWT avec des pywavelets à faire les deux dans Pytorch_Wavelets, en utilisant un GTX1080. Les méthodes Numpy ont été exécutées sur une machine Xeon PHI à 14 noyaux en utilisant le python parallèle d'Intel. Pour le DTWCWT, nous utilisons les filtres Near_Sym_A pour la première échelle et les filtres QShift_A pour les échelles suivantes. Pour le DWT, nous utilisons les filtres DB4.
Pour une taille d'entrée fixe, mais variant le nombre d'échelles (de 1 à 4), nous avons les vitesses suivantes (en moyenne sur 5 courses):
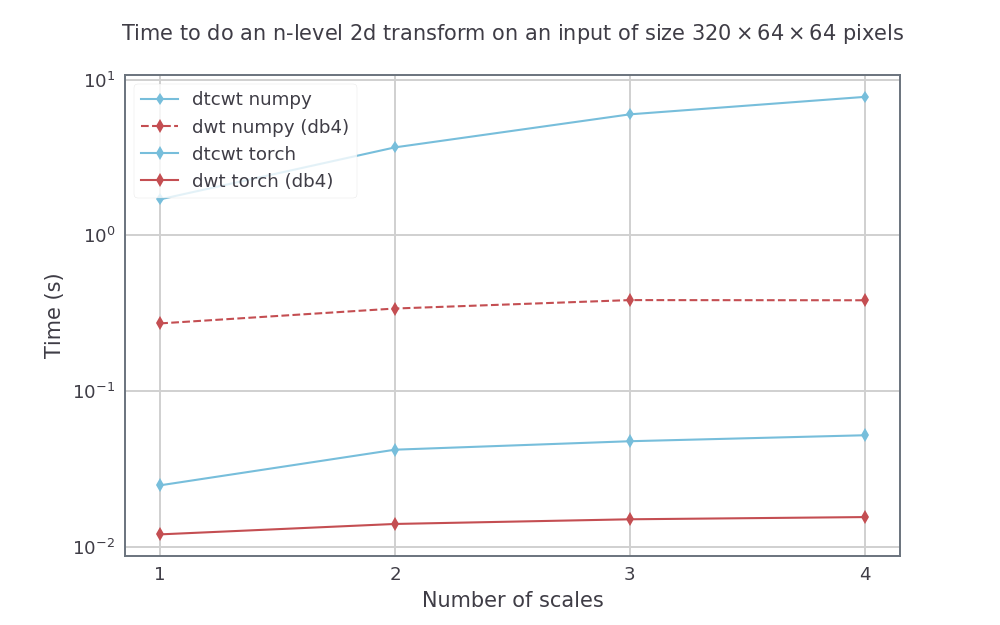
Pour une taille d'entrée avec la hauteur et la largeur 512 par 512, nous faisons également varier la taille du lot pour une transformée à 3 échelles. Les vitesses résultantes étaient:
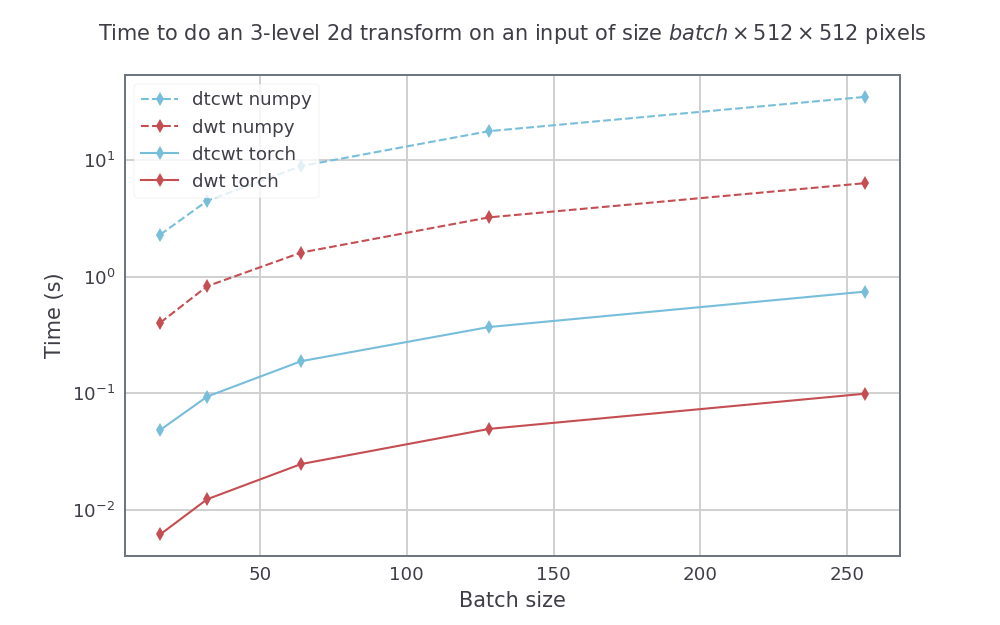
La façon la plus simple d'installer pytorch_wavelets est de cloner le repo et de l'installer. Les versions ultérieures seront publiées sur PYPI, mais les documents doivent d'abord être mis à jour:
$ git clone https://github.com/fbcotter/pytorch_wavelets $ cd pytorch_wavelets $ PIP Install.
(Bien que la commande de développement puisse être plus utile si vous avez l'intention d'effectuer une modification significative de la bibliothèque.) Une suite de tests est fournie afin que vous puissiez vérifier que le code fonctionne sur votre système:
$ pip install -r tests / exigences.txt $ tests pytest /
Pour le DWT - Notez que la sortie High Pass a une dimension supplémentaire, dans laquelle nous empilons les coefficients (LH, HL, HH). Notez également que la sortie YH a d'abord les meilleurs coefficients de détail et le dernier le plus grossier (l'opposé aux pywavelettes).
import torch
from pytorch_wavelets import DWTForward , DWTInverse
xfm = DWTForward ( J = 3 , wave = 'db3' , mode = 'zero' )
X = torch . randn ( 10 , 5 , 64 , 64 )
Yl , Yh = xfm ( X )
print ( Yl . shape )
> >> torch . Size ([ 10 , 5 , 12 , 12 ])
print ( Yh [ 0 ]. shape )
> >> torch . Size ([ 10 , 5 , 3 , 34 , 34 ])
print ( Yh [ 1 ]. shape )
> >> torch . Size ([ 10 , 5 , 3 , 19 , 19 ])
print ( Yh [ 2 ]. shape )
> >> torch . Size ([ 10 , 5 , 3 , 12 , 12 ])
ifm = DWTInverse ( wave = 'db3' , mode = 'zero' )
Y = ifm (( Yl , Yh ))Pour le DTCWT:
import torch
from pytorch_wavelets import DTCWTForward , DTCWTInverse
xfm = DTCWTForward ( J = 3 , biort = 'near_sym_b' , qshift = 'qshift_b' )
X = torch . randn ( 10 , 5 , 64 , 64 )
Yl , Yh = xfm ( X )
print ( Yl . shape )
> >> torch . Size ([ 10 , 5 , 16 , 16 ])
print ( Yh [ 0 ]. shape )
> >> torch . Size ([ 10 , 5 , 6 , 32 , 32 , 2 ])
print ( Yh [ 1 ]. shape )
> >> torch . Size ([ 10 , 5 , 6 , 16 , 16 , 2 ])
print ( Yh [ 2 ]. shape )
> >> torch . Size ([ 10 , 5 , 6 , 8 , 8 , 2 ])
ifm = DTCWTInverse ( biort = 'near_sym_b' , qshift = 'qshift_b' )
Y = ifm (( Yl , Yh ))Quelques notes initiales:
Cela ne devrait pas surprendre les utilisateurs de Pytorch. Les transformations DWT et DTCWT prennent en charge Cuda Calling:
import torch
from pytorch_wavelets import DTCWTForward , DTCWTInverse
xfm = DTCWTForward ( J = 3 , biort = 'near_sym_b' , qshift = 'qshift_b' ). cuda ()
X = torch . randn ( 10 , 5 , 64 , 64 ). cuda ()
Yl , Yh = xfm ( X )
ifm = DTCWTInverse ( biort = 'near_sym_b' , qshift = 'qshift_b' ). cuda ()
Y = ifm (( Yl , Yh )) Les tests automatisés ne peuvent pas tester la fonctionnalité GPU, mais vérifiez l'exécution du processeur. Pour tester si le dépôt fonctionne sur votre GPU, vous pouvez télécharger le référentiel, assurer que vous avez Pytorch avec CUDA activé (les tests vérifieront si torch.cuda.is_available() renvoie true) et exécuter:
pip install -r tests / exigences.txt tests pytest /
De la base du repo.
Il est possible de passer des gradients à travers les transformations vers l'avant et vers l'arrière. Tout ce que vous avez à faire est de vous assurer que l'entrée à chacun a le réglage d'attribut requis_grate sur true.
Basé sur le pack de transformation d'ondelettes complexes à double arbre pour Matlab par Nick Kingsbury, Cambridge University. La lecture originale peut être trouvée dans original_readme.txt. Ce fichier décrit les conditions d'utilisation de la boîte à outils MATLAB d'origine.
De plus amples informations sur le DT CWT peuvent être obtenues à partir de documents téléchargeables à partir de mon site Web (ci-dessous). Le meilleur tutoriel est dans le journal de la Royal Society 1999. En particulier, cela explique la conversion entre les sous-images quad numéro et les paires de sous-images complexes. Les filtres Q-Shift sont expliqués dans l'article ICIP 2000 et plus en détail dans l'article de mai 2001 pour le Journal on Applied and Computational Harmonic Analysis.
Ce code est copyright et est fourni gratuitement à des fins de recherche uniquement. En échange de la fourniture du code, tout ce que je demande, c'est que si vous utilisez les algorithmes, vous faites référence à ce travail dans tous les articles que vous écrivez et que vous me faites savoir si vous trouvez de bonnes applications pour le DT CWT. Si les applications sont bonnes, je serais très intéressé par la collaboration. J'accepte aucune responsabilité résultant de l'utilisation de ces algorithmes.
Nick Kingsbury, Cambridge University, juin 2003.
Dr Ng Kingsbury, Dept. of Engineering, University of Cambridge, Trumpington St., Cambridge CB2 1PZ, Royaume-Uni., Ou Trinity College, Cambridge CB2 1TQ, Royaume-Uni. Téléphone: (0 ou +44) 1223 338514/332647; Accueil: 1954 211152; Fax: 1223 338564/332662; E-mail: [email protected] Page d'accueil Web: http://www.eng.cam.ac.uk/~ngk/