Die vollständige Dokumentation ist auch hier verfügbar.
Dieses Paket unterstützt die Berechnung des 2D Discreten Wavelet und des 2D-Dual-Tree-Komplex-Wavelet-Transformationen, deren Inversen und Durchgang von Gradienten durch beide mit Pytorch.
Die Implementierung ist so konzipiert, dass sie mit Chargen von Mehrkanalbildern verwendet werden soll. Wir verwenden die Standard -Pytorch -Implementierung des Datenformats von NCHW.
Wir haben auch Ebenen hinzugefügt, um das 2-D-DTCWT-basierte Scatternet durchzuführen. Dies ähnelt dem Morlet -Basis -Streitennetz in Kymatio, ist jedoch ungefähr 10 -mal schneller.
Wenn Sie dieses Repo verwenden, zitieren Sie bitte meine Doktorarbeit, Kapitel 3: https://doi.org/10.17863/cam.53748.
import torch
from pytorch_wavelets import DWT1DForward , DWT1DInverse # or simply DWT1D, IDWT1D
dwt = DWT1DForward ( wave = 'db6' , J = 3 )
X = torch . randn ( 10 , 5 , 100 )
yl , yh = dwt ( X )
print ( yl . shape )
> >> torch . Size ([ 10 , 5 , 22 ])
print ( yh [ 0 ]. shape )
> >> torch . Size ([ 10 , 5 , 55 ])
print ( yh [ 1 ]. shape )
> >> torch . Size ([ 10 , 5 , 33 ])
print ( yh [ 2 ]. shape )
> >> torch . Size ([ 10 , 5 , 22 ])
idwt = DWT1DInverse ( wave = 'db6' )
x = idwt (( yl , yh )) import torch
from pytorch_wavelets import ScatLayer
scat = ScatLayer ()
X = torch . randn ( 10 , 5 , 64 , 64 )
# A first order scatternet with 6 orientations and one lowpass channels
# gives 7 times the input channel dimension
Z = scat ( X )
print ( Z . shape )
> >> torch . Size ([ 10 , 35 , 32 , 32 ])
# A second order scatternet with 6 orientations and one lowpass channels
# gives 7^2 times the input channel dimension
scat2 = torch . nn . Sequential ( ScatLayer (), ScatLayer ())
Z = scat2 ( X )
print ( Z . shape )
> >> torch . Size ([ 10 , 245 , 16 , 16 ])
# We also have a slightly more specialized, but slower, second order scatternet
from pytorch_wavelets import ScatLayerj2
scat2a = ScatLayerj2 ()
Z = scat2a ( X )
print ( Z . shape )
> >> torch . Size ([ 10 , 245 , 16 , 16 ])
# These all of course work with cuda
scat2a . cuda ()
Z = scat2a ( X . cuda ())Version 1.0.0 hat nun Unterstützung für die trennbare DWT -Berechnung und mehr Polsterschemata wie symmetrisch, Null und Periodisierung hinzugefügt.
Sie müssen auch nicht mehr die Anzahl der Kanäle angeben, wenn Sie die Wavelet -Transformationsklassen erstellen.
Wir vergleichen das DTCWT mit dem Python -Paket und das DWT mit PyWavelets, um beide in Pytorch_Wavelets mit einem GTX1080 zu machen. Die Numpy -Methoden wurden auf einer 14 Core Xeon Phi -Maschine unter Verwendung von Intel Parallel Python ausgeführt. Für das DTWCWT verwenden wir die Filter von nahe_sym_a für die erste Skala und die QSHIFT_A -Filter für nachfolgende Skalen. Für die DWT verwenden wir die DB4 -Filter.
Für eine feste Eingangsgröße, aber die Anzahl der Skalen (von 1 bis 4) haben die folgenden Geschwindigkeiten (gemittelt über 5 Läufe):
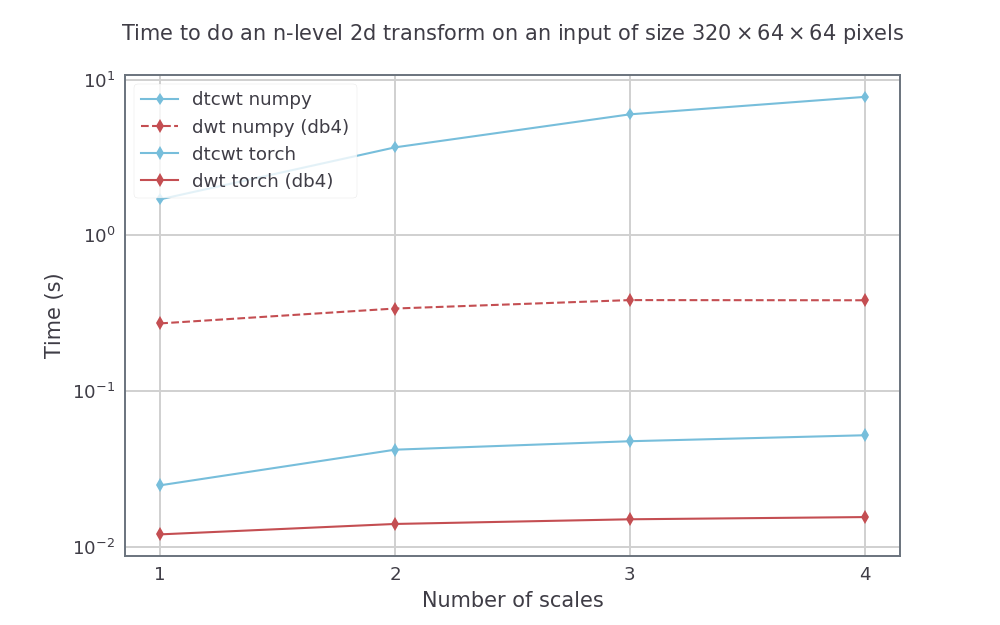
Für eine Eingangsgröße mit Höhe und Breite 512 bis 512 variieren wir auch die Chargengröße für eine 3 -Skalierungs -Transformation. Die resultierenden Geschwindigkeiten waren:
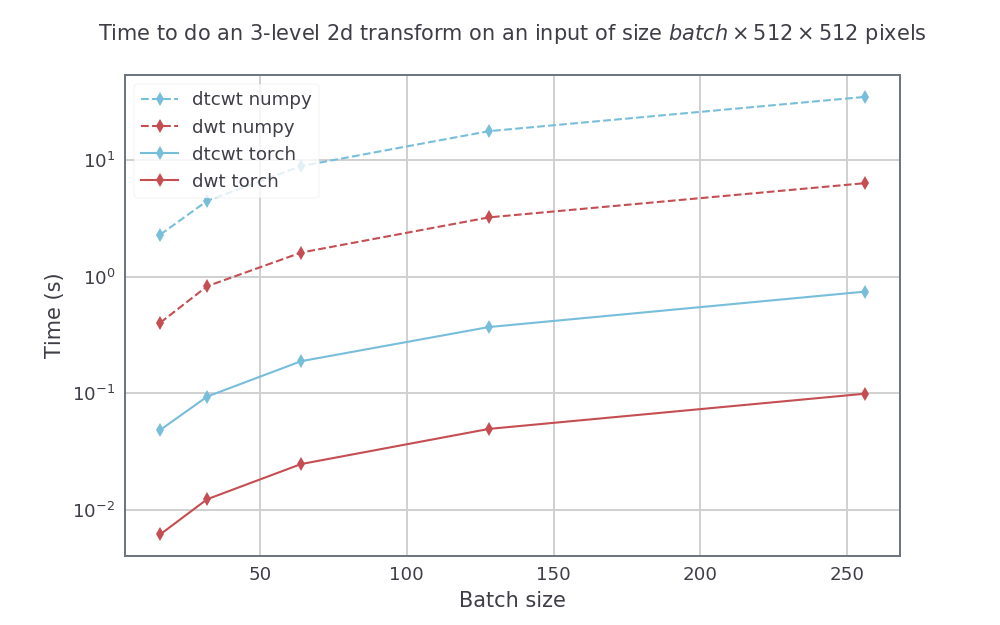
Der einfachste Weg, pytorch_wavelets zu installieren, besteht darin, das Repo zu klonen und zu pip installieren. Spätere Versionen werden auf PYPI veröffentlicht, aber die Dokumente müssen zuerst aktualisiert werden:
$ Git Clone https://github.com/fbcotter/pytorch_wavelets $ cd pytorch_wavelets $ pip install.
(Der Befehl entwickelte möglicherweise nützlicher, wenn Sie beabsichtigen, eine erhebliche Änderung in der Bibliothek vorzunehmen.) Eine Testsuite wird bereitgestellt, damit Sie überprüfen können, ob der Code in Ihrem System funktioniert:
$ pip install -R -Tests/Anforderungen.txt $ pytest Tests/
Beachten Sie für die DWT - Beachten Sie, dass die Hochpassausgabe eine zusätzliche Dimension hat, in der wir die (LH, HL, HH) Koeffizienten stapeln. Beachten Sie auch, dass die YH -Ausgabe zuerst die besten Detailkoeffizienten und das koarsste zuletzt (das Gegenteil von Pywavelets) aufweist.
import torch
from pytorch_wavelets import DWTForward , DWTInverse
xfm = DWTForward ( J = 3 , wave = 'db3' , mode = 'zero' )
X = torch . randn ( 10 , 5 , 64 , 64 )
Yl , Yh = xfm ( X )
print ( Yl . shape )
> >> torch . Size ([ 10 , 5 , 12 , 12 ])
print ( Yh [ 0 ]. shape )
> >> torch . Size ([ 10 , 5 , 3 , 34 , 34 ])
print ( Yh [ 1 ]. shape )
> >> torch . Size ([ 10 , 5 , 3 , 19 , 19 ])
print ( Yh [ 2 ]. shape )
> >> torch . Size ([ 10 , 5 , 3 , 12 , 12 ])
ifm = DWTInverse ( wave = 'db3' , mode = 'zero' )
Y = ifm (( Yl , Yh ))Für die DTCWT:
import torch
from pytorch_wavelets import DTCWTForward , DTCWTInverse
xfm = DTCWTForward ( J = 3 , biort = 'near_sym_b' , qshift = 'qshift_b' )
X = torch . randn ( 10 , 5 , 64 , 64 )
Yl , Yh = xfm ( X )
print ( Yl . shape )
> >> torch . Size ([ 10 , 5 , 16 , 16 ])
print ( Yh [ 0 ]. shape )
> >> torch . Size ([ 10 , 5 , 6 , 32 , 32 , 2 ])
print ( Yh [ 1 ]. shape )
> >> torch . Size ([ 10 , 5 , 6 , 16 , 16 , 2 ])
print ( Yh [ 2 ]. shape )
> >> torch . Size ([ 10 , 5 , 6 , 8 , 8 , 2 ])
ifm = DTCWTInverse ( biort = 'near_sym_b' , qshift = 'qshift_b' )
Y = ifm (( Yl , Yh ))Einige erste Notizen:
Dies sollte für Pytorch -Benutzer keine Überraschung sein. Die DWT- und DTCWT -Transformationen unterstützen Cuda Calling:
import torch
from pytorch_wavelets import DTCWTForward , DTCWTInverse
xfm = DTCWTForward ( J = 3 , biort = 'near_sym_b' , qshift = 'qshift_b' ). cuda ()
X = torch . randn ( 10 , 5 , 64 , 64 ). cuda ()
Yl , Yh = xfm ( X )
ifm = DTCWTInverse ( biort = 'near_sym_b' , qshift = 'qshift_b' ). cuda ()
Y = ifm (( Yl , Yh )) Die automatisierten Tests können die GPU -Funktionalität nicht testen, sondern überprüft die CPU ausgeführt. Um zu testen, ob das Repo an Ihrer GPU arbeitet, können Sie das Repo herunterladen, stellen Sie sicher, dass Sie Pytorch mit aktiviertem CUDA -aktiviert haben (die Tests prüfen, ob torch.cuda.is_available() true zurückgibt) und rennen Sie aus:
PIP -Installation -r -Tests/Anforderungen.txt PyTest -Tests/
Aus der Basis des Repo.
Es ist möglich, Gradienten durch die Vorwärts- und Rückwärtsveränderungen zu bringen. Alles, was Sie tun müssen, ist sicherzustellen, dass die Eingabe für jedes für das erforderliche Attribut auf true eingestellt ist.
Basierend auf dem Dual-Tree-Komplex-Wavelet-Transformationspaket für MATLAB von Nick Kingsbury, Universität Cambridge. Die ursprüngliche Readme finden Sie in Original_Readme.txt. Diese Datei beschreibt die Verwendung der ursprünglichen MATLAB -Toolbox.
Weitere Informationen zum DT -CWT finden Sie aus Papieren, die von meiner Website heruntergeladen werden können (unten angegeben). Das beste Tutorial ist das Papier der Royal Society von 1999. Insbesondere erläutert dies die Umwandlung zwischen "realen" Quad-Nummer-Subimages und Paaren komplexer Unterimages. Die Q-Shift-Filter werden im ICIP 2000-Artikel und im Mai 2001 im Mai 2001 für das Journal on Applied and Computational Harmonic Analysis erläutert.
Dieser Code ist urheberrechtlich geschützt und wird nur für Forschungszwecke kostenlos geliefert. Als Gegenleistung für die Lieferung des Codes frage ich nur, dass Sie, wenn Sie die Algorithmen verwenden, in allen Arbeiten, die Sie schreiben, den gebührenden Hinweis auf diese Arbeit geben und dass Sie mich wissen lassen, wenn Sie gute Bewerbungen für das DT -CWT finden. Wenn die Bewerbungen gut sind, wäre ich sehr an Zusammenarbeit interessiert. Ich übernehme keine Haftung, die sich aus der Verwendung dieser Algorithmen ergibt.
Nick Kingsbury, Cambridge University, Juni 2003.
Dr. Ng Kingsbury, Abteilung für Ingenieurwesen, Universität von Cambridge, Trumpington St., Cambridge CB2 1pz, Großbritannien, oder Trinity College, Cambridge CB2 1TQ, Großbritannien. Telefon: (0 oder +44) 1223 338514 /332647; Heimat: 1954 211152; Fax: 1223 338564 /332662; E-Mail: [email protected] Web-Homepage: http://www.eng.cam.ac.uk/~ngk/