完整的文档也可以在此处提供。
该软件包为计算2D离散小波和2D双树复合小波的变换,它们的对倒置以及通过Pytorch的传递梯度提供了支持。
该实现旨在与多通道图像批量一起使用。我们使用具有“ NCHW”数据格式的标准Pytorch实现。
我们还添加了层以进行2-D DTCWT的散点网。这类似于Kymatio中Morlet的散点网,但大约要快10倍。
如果您使用此回购,请引用我的博士学位论文,第3章:https://doi.org/10.17863/cam.53748。
import torch
from pytorch_wavelets import DWT1DForward , DWT1DInverse # or simply DWT1D, IDWT1D
dwt = DWT1DForward ( wave = 'db6' , J = 3 )
X = torch . randn ( 10 , 5 , 100 )
yl , yh = dwt ( X )
print ( yl . shape )
> >> torch . Size ([ 10 , 5 , 22 ])
print ( yh [ 0 ]. shape )
> >> torch . Size ([ 10 , 5 , 55 ])
print ( yh [ 1 ]. shape )
> >> torch . Size ([ 10 , 5 , 33 ])
print ( yh [ 2 ]. shape )
> >> torch . Size ([ 10 , 5 , 22 ])
idwt = DWT1DInverse ( wave = 'db6' )
x = idwt (( yl , yh )) import torch
from pytorch_wavelets import ScatLayer
scat = ScatLayer ()
X = torch . randn ( 10 , 5 , 64 , 64 )
# A first order scatternet with 6 orientations and one lowpass channels
# gives 7 times the input channel dimension
Z = scat ( X )
print ( Z . shape )
> >> torch . Size ([ 10 , 35 , 32 , 32 ])
# A second order scatternet with 6 orientations and one lowpass channels
# gives 7^2 times the input channel dimension
scat2 = torch . nn . Sequential ( ScatLayer (), ScatLayer ())
Z = scat2 ( X )
print ( Z . shape )
> >> torch . Size ([ 10 , 245 , 16 , 16 ])
# We also have a slightly more specialized, but slower, second order scatternet
from pytorch_wavelets import ScatLayerj2
scat2a = ScatLayerj2 ()
Z = scat2a ( X )
print ( Z . shape )
> >> torch . Size ([ 10 , 245 , 16 , 16 ])
# These all of course work with cuda
scat2a . cuda ()
Z = scat2a ( X . cuda ())版本1.0.0现在添加了对可分离DWT计算的支持,以及更多的填充方案,例如对称,零和分期。
同样,在创建小波变换类时,不再需要指定通道数。
我们将DTCWT与Python包进行比较,并使用GTX1080在Pytorch_wavelets中进行DWT进行DWT进行比较。使用英特尔的平行python,在14核Xeon Phi机器上运行Numpy方法。对于DTWCWT,我们将近_sym_a滤波器用于第一刻度和QSHIFT_A滤波器以进行后续尺度。对于DWT,我们使用DB4过滤器。
对于固定的输入尺寸,但是改变了尺度的数量(从1到4),我们的速度(平均为5个运行):
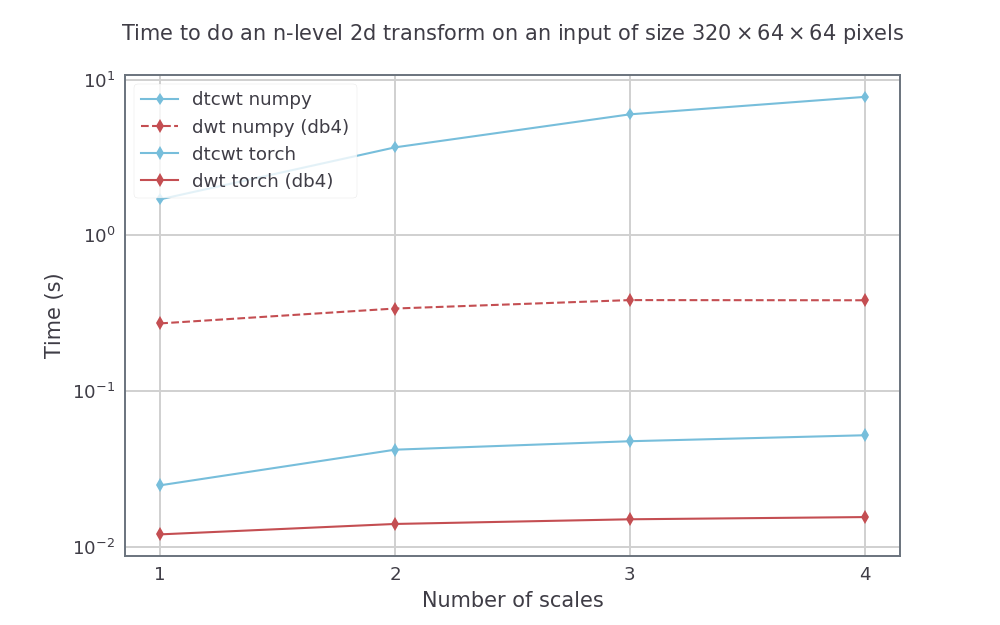
对于具有高度和宽度512 x 512的输入尺寸,我们还可以改变3刻度转换的批次大小。由此产生的速度是:
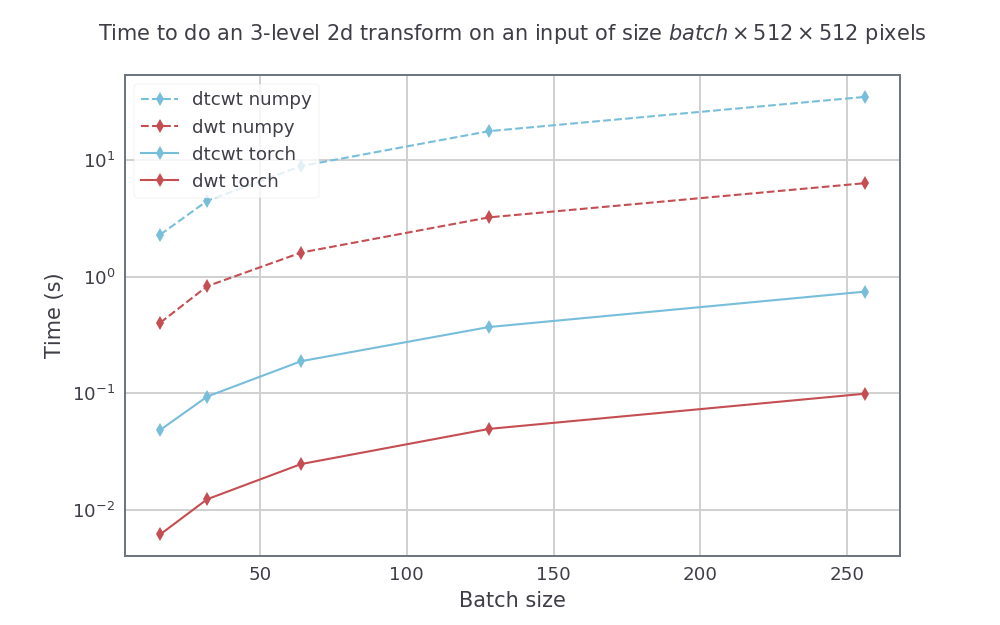
安装pytorch_wavelets的最简单方法是克隆回购并安装PIP。以后的版本将在PYPI上发布,但文档需要首先更新:
$ git克隆https://github.com/fbcotter/pytorch_wavelets $ cd pytorch_wavelets $ pip安装。
(尽管如果您打算对库进行任何重大修改,则开发命令可能会更有用。)提供了测试套件,以便您可以验证系统上的代码工作:
$ pip install -r tests/supports.txt $ PYTEST测试/
对于DWT-请注意,高通输出具有额外的尺寸,其中我们将(LH,HL,HH)系数堆叠起来。另请注意,YH输出首先具有最好的细节系数,而最粗糙的系数则是最高的(与Pywavelets相反)。
import torch
from pytorch_wavelets import DWTForward , DWTInverse
xfm = DWTForward ( J = 3 , wave = 'db3' , mode = 'zero' )
X = torch . randn ( 10 , 5 , 64 , 64 )
Yl , Yh = xfm ( X )
print ( Yl . shape )
> >> torch . Size ([ 10 , 5 , 12 , 12 ])
print ( Yh [ 0 ]. shape )
> >> torch . Size ([ 10 , 5 , 3 , 34 , 34 ])
print ( Yh [ 1 ]. shape )
> >> torch . Size ([ 10 , 5 , 3 , 19 , 19 ])
print ( Yh [ 2 ]. shape )
> >> torch . Size ([ 10 , 5 , 3 , 12 , 12 ])
ifm = DWTInverse ( wave = 'db3' , mode = 'zero' )
Y = ifm (( Yl , Yh ))对于DTCWT:
import torch
from pytorch_wavelets import DTCWTForward , DTCWTInverse
xfm = DTCWTForward ( J = 3 , biort = 'near_sym_b' , qshift = 'qshift_b' )
X = torch . randn ( 10 , 5 , 64 , 64 )
Yl , Yh = xfm ( X )
print ( Yl . shape )
> >> torch . Size ([ 10 , 5 , 16 , 16 ])
print ( Yh [ 0 ]. shape )
> >> torch . Size ([ 10 , 5 , 6 , 32 , 32 , 2 ])
print ( Yh [ 1 ]. shape )
> >> torch . Size ([ 10 , 5 , 6 , 16 , 16 , 2 ])
print ( Yh [ 2 ]. shape )
> >> torch . Size ([ 10 , 5 , 6 , 8 , 8 , 2 ])
ifm = DTCWTInverse ( biort = 'near_sym_b' , qshift = 'qshift_b' )
Y = ifm (( Yl , Yh ))一些初始注释:
对于Pytorch用户来说,这不足为奇。 DWT和DTCWT转换支持CUDA调用:
import torch
from pytorch_wavelets import DTCWTForward , DTCWTInverse
xfm = DTCWTForward ( J = 3 , biort = 'near_sym_b' , qshift = 'qshift_b' ). cuda ()
X = torch . randn ( 10 , 5 , 64 , 64 ). cuda ()
Yl , Yh = xfm ( X )
ifm = DTCWTInverse ( biort = 'near_sym_b' , qshift = 'qshift_b' ). cuda ()
Y = ifm (( Yl , Yh ))自动测试无法测试GPU功能,但请检查CPU运行。要测试存储库是否正在处理您的GPU,您可以下载仓库,确保您使用启用CUDA的Pytorch(测试将检查torch.cuda.is_available()是否返回true),然后运行:
PIP安装-R测试/需求.txt pytest测试/
从存储库的底部。
可以将梯度通过前向和向后变换。您需要做的就是确保每个对每个的输入设置为true。
基于剑桥大学尼克·金斯伯里(Nick Kingsbury)的MATLAB的双树复杂小波变换包。可以在Original_readme.txt中找到原始读数。该文件概述了原始MATLAB工具箱的使用条件。
有关DT CWT的更多信息,可以从可从我的网站下载的论文获得(下面给出)。最好的教程是在1999年的皇家学会论文中。特别是这解释了“真实”四肢 - 数字子图像与复杂子图的对之间的转换。 Q-Shift过滤器在ICIP 2000论文中进行了解释,并在2001年5月的《应用和计算谐波分析》杂志的《 2001年5月论文》中进行了详细说明。
该代码是版权,仅用于研究目的免费提供。作为提供代码的回报,我要问的是,如果您使用算法,则在您撰写的任何论文中给出了适当的参考,并让我知道是否找到了DT CWT的任何好应用。如果应用程序很好,我将对协作非常感兴趣。我不接受使用这些算法而产生的责任。
尼克·金斯伯里(Nick Kingsbury),剑桥大学,2003年6月。
剑桥大学,特朗普顿街,英国剑桥CB2 1pz。电话:(0或+44)1223 338514 /332647;主页:1954 211152;传真:1223 338564 /332662;电子邮件:[email protected]网络主页:http://www.eng.cam.ac.uk/~ngk/