La documentación completa también está disponible aquí.
Este paquete proporciona soporte para calcular la wavelet discreta 2D y las transformaciones de wavelet complejo 2D de doble árbol, sus inversos y gradientes que pasan a través de ambos usando Pytorch.
La implementación está diseñada para usarse con lotes de imágenes multicanal. Utilizamos la implementación estándar de Pytorch de tener formato de datos 'NCHW'.
También hemos agregado capas para hacer la dispersión basada en DTCWT 2-D. Esto es similar a la dispersión basada en Morlet en Kymatio, pero es aproximadamente 10 veces más rápido.
Si usa este repositorio, cite mi tesis de doctorado, Capítulo 3: https://doi.org/10.17863/cam.53748.
import torch
from pytorch_wavelets import DWT1DForward , DWT1DInverse # or simply DWT1D, IDWT1D
dwt = DWT1DForward ( wave = 'db6' , J = 3 )
X = torch . randn ( 10 , 5 , 100 )
yl , yh = dwt ( X )
print ( yl . shape )
> >> torch . Size ([ 10 , 5 , 22 ])
print ( yh [ 0 ]. shape )
> >> torch . Size ([ 10 , 5 , 55 ])
print ( yh [ 1 ]. shape )
> >> torch . Size ([ 10 , 5 , 33 ])
print ( yh [ 2 ]. shape )
> >> torch . Size ([ 10 , 5 , 22 ])
idwt = DWT1DInverse ( wave = 'db6' )
x = idwt (( yl , yh )) import torch
from pytorch_wavelets import ScatLayer
scat = ScatLayer ()
X = torch . randn ( 10 , 5 , 64 , 64 )
# A first order scatternet with 6 orientations and one lowpass channels
# gives 7 times the input channel dimension
Z = scat ( X )
print ( Z . shape )
> >> torch . Size ([ 10 , 35 , 32 , 32 ])
# A second order scatternet with 6 orientations and one lowpass channels
# gives 7^2 times the input channel dimension
scat2 = torch . nn . Sequential ( ScatLayer (), ScatLayer ())
Z = scat2 ( X )
print ( Z . shape )
> >> torch . Size ([ 10 , 245 , 16 , 16 ])
# We also have a slightly more specialized, but slower, second order scatternet
from pytorch_wavelets import ScatLayerj2
scat2a = ScatLayerj2 ()
Z = scat2a ( X )
print ( Z . shape )
> >> torch . Size ([ 10 , 245 , 16 , 16 ])
# These all of course work with cuda
scat2a . cuda ()
Z = scat2a ( X . cuda ())La versión 1.0.0 ahora ha agregado soporte para el cálculo de DWT separable y más esquemas de relleno, como simétrico, cero y periodización.
Además, ya no es necesario especificar el número de canales al crear las clases de transformación Wavelet.
Comparamos hacer el DTCWT con el paquete Python y hacer el DWT con Pywavelets para hacer ambas cosas en Pytorch_wavelets, usando un GTX1080. Los métodos numpy se ejecutaron en una máquina Xeon Phi de 14 núcleos utilizando la pitón paralela de Intel. Para el DTWCWT usamos los filtros cercanos_sym_a para la primera escala y los filtros QSHIFT_A para escalas posteriores. Para el DWT usamos los filtros DB4.
Para un tamaño de entrada fijo, pero variando el número de escalas (de 1 a 4) tenemos las siguientes velocidades (promediadas en más de 5 corridas):
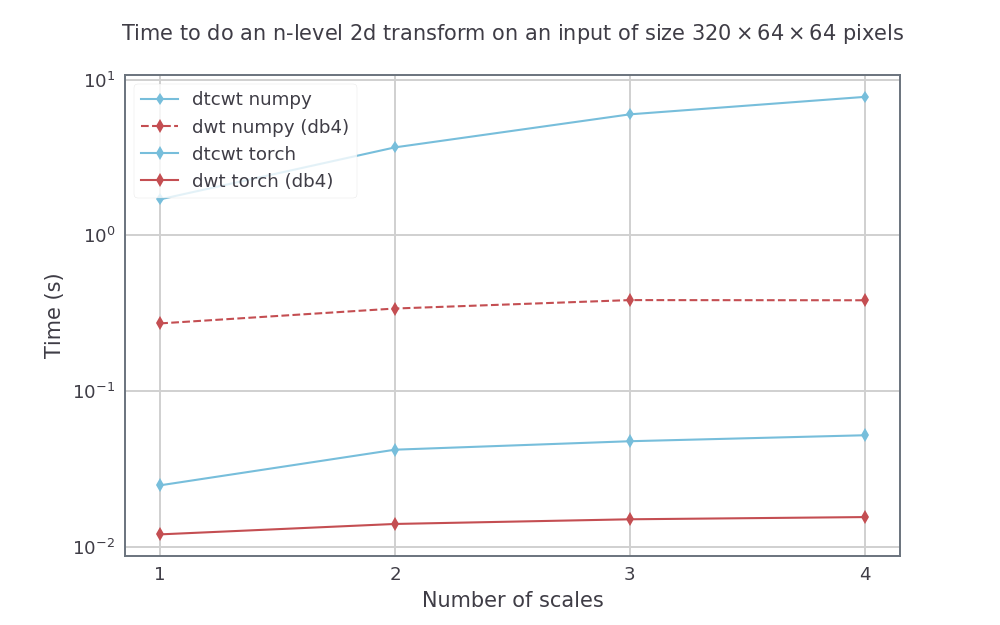
Para un tamaño de entrada con altura y ancho 512 por 512, también variamos el tamaño de lotes para una transformación de 3 escala. Las velocidades resultantes fueron:
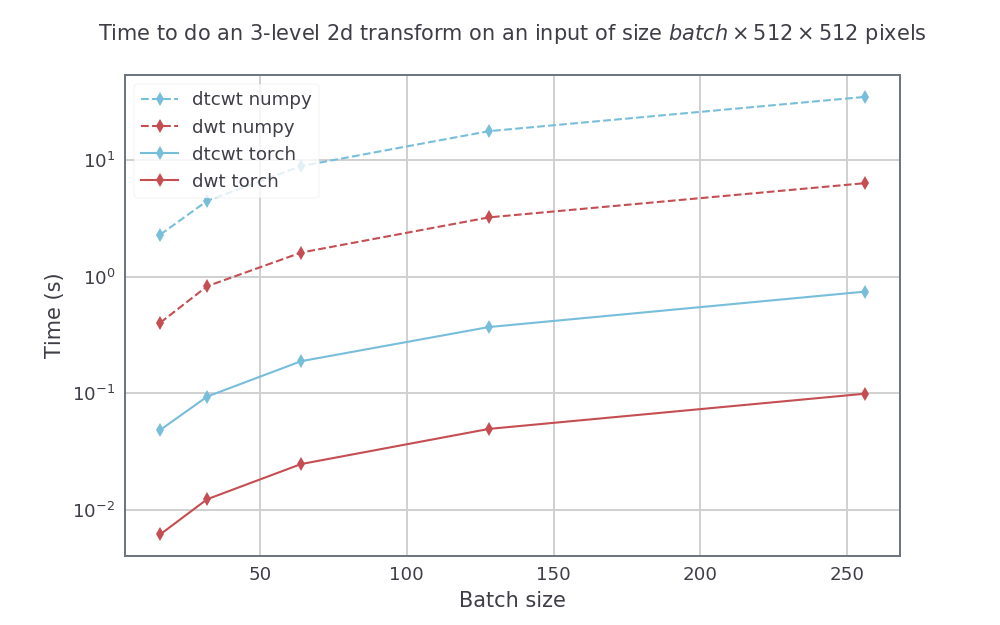
La forma más fácil de instalar pytorch_wavelets es clonar el repositorio y PIP instalarlo. Las versiones posteriores se lanzarán en PYPI, pero los documentos deben actualizarse primero:
$ git clone https://github.com/fbcotter/pytorch_wavelets $ cd pytorch_wavelets $ PIP Instalar.
(Aunque el comando de desarrollo puede ser más útil si tiene la intención de realizar cualquier modificación significativa en la biblioteca). Se proporciona un conjunto de pruebas para que pueda verificar el código funciona en su sistema:
$ PIP Install -R Pruebas/requisitos.txt $ Pytest Pruebas/
Para el DWT, tenga en cuenta que la salida de paso alto tiene una dimensión adicional, en la que apilamos los coeficientes (LH, HL, HH). También tenga en cuenta que la salida YH tiene los mejores coeficientes de detalles primero, y el más grueso final (lo contrario a Pywavelets).
import torch
from pytorch_wavelets import DWTForward , DWTInverse
xfm = DWTForward ( J = 3 , wave = 'db3' , mode = 'zero' )
X = torch . randn ( 10 , 5 , 64 , 64 )
Yl , Yh = xfm ( X )
print ( Yl . shape )
> >> torch . Size ([ 10 , 5 , 12 , 12 ])
print ( Yh [ 0 ]. shape )
> >> torch . Size ([ 10 , 5 , 3 , 34 , 34 ])
print ( Yh [ 1 ]. shape )
> >> torch . Size ([ 10 , 5 , 3 , 19 , 19 ])
print ( Yh [ 2 ]. shape )
> >> torch . Size ([ 10 , 5 , 3 , 12 , 12 ])
ifm = DWTInverse ( wave = 'db3' , mode = 'zero' )
Y = ifm (( Yl , Yh ))Para el dtcwt:
import torch
from pytorch_wavelets import DTCWTForward , DTCWTInverse
xfm = DTCWTForward ( J = 3 , biort = 'near_sym_b' , qshift = 'qshift_b' )
X = torch . randn ( 10 , 5 , 64 , 64 )
Yl , Yh = xfm ( X )
print ( Yl . shape )
> >> torch . Size ([ 10 , 5 , 16 , 16 ])
print ( Yh [ 0 ]. shape )
> >> torch . Size ([ 10 , 5 , 6 , 32 , 32 , 2 ])
print ( Yh [ 1 ]. shape )
> >> torch . Size ([ 10 , 5 , 6 , 16 , 16 , 2 ])
print ( Yh [ 2 ]. shape )
> >> torch . Size ([ 10 , 5 , 6 , 8 , 8 , 2 ])
ifm = DTCWTInverse ( biort = 'near_sym_b' , qshift = 'qshift_b' )
Y = ifm (( Yl , Yh ))Algunas notas iniciales:
Esto no debería sorprender a los usuarios de Pytorch. El DWT y DTCWT transforman el soporte de CUDA llamadas:
import torch
from pytorch_wavelets import DTCWTForward , DTCWTInverse
xfm = DTCWTForward ( J = 3 , biort = 'near_sym_b' , qshift = 'qshift_b' ). cuda ()
X = torch . randn ( 10 , 5 , 64 , 64 ). cuda ()
Yl , Yh = xfm ( X )
ifm = DTCWTInverse ( biort = 'near_sym_b' , qshift = 'qshift_b' ). cuda ()
Y = ifm (( Yl , Yh )) Las pruebas automatizadas no pueden probar la funcionalidad de la GPU, pero verifique la ejecución de la CPU. Para probar si el repositorio está funcionando en su GPU, puede descargar el repositorio, asegúrese de tener Pytorch con CUDA habilitado (las pruebas verificarán si torch.cuda.is_available() devuelve verdadero) y ejecutar:
PIP install -r pruebas/requisitos.txt pruebas de pytest/
De la base del repositorio.
Es posible pasar los gradientes a través de las transformaciones hacia adelante y hacia atrás. Todo lo que necesita hacer es asegurarse de que la entrada a cada uno tenga el atributo requerido_grad establecido en True.
Basado en el paquete de transformación wavelet complejo de doble árbol para Matlab por Nick Kingsbury, Universidad de Cambridge. El ReadMe original se puede encontrar en original_readme.txt. Este archivo describe las condiciones de uso de la caja de herramientas MATLAB original.
Se puede obtener más información sobre el DT CWT de los documentos que se pueden descargar desde mi sitio web (que se proporciona a continuación). El mejor tutorial es en el artículo de la Royal Society de 1999. En particular, esto explica la conversión entre las subimages de número quad 'real' y los pares de subimes complejas. Los filtros Q-Shift se explican en el documento ICIP 2000 y con más detalle en el documento de mayo de 2001 para la revista sobre análisis armónico aplicado y computacional.
Este código es derechos de autor y se suministra de forma gratuita solo para fines de investigación. A cambio de suministrar el código, todo lo que pregunto es que, si usa los algoritmos, le da referencia a este trabajo en cualquier documento que escriba y que me haga saber si encuentra alguna buena aplicación para el DT CWT. Si las aplicaciones son buenas, estaría muy interesado en la colaboración. No acepto ninguna responsabilidad derivada del uso de estos algoritmos.
Nick Kingsbury, Universidad de Cambridge, junio de 2003.
Dr. Ng Kingsbury, Departamento de Ingeniería, Universidad de Cambridge, Trumpington St., Cambridge CB2 1PZ, Reino Unido, o Trinity College, Cambridge CB2 1TQ, Reino Unido. Teléfono: (0 o +44) 1223 338514 /332647; Inicio: 1954 211152; Fax: 1223 338564 /332662; Correo electrónico: [email protected] Página de inicio web: http://www.eng.cam.ac.uk/~ngk/