Space Simulation下載 - Space Simulation源代碼下載

Space Simulation

其他源碼

1.0.0

下載

空間模擬

查看演示·報告錯誤·請求功能

介紹

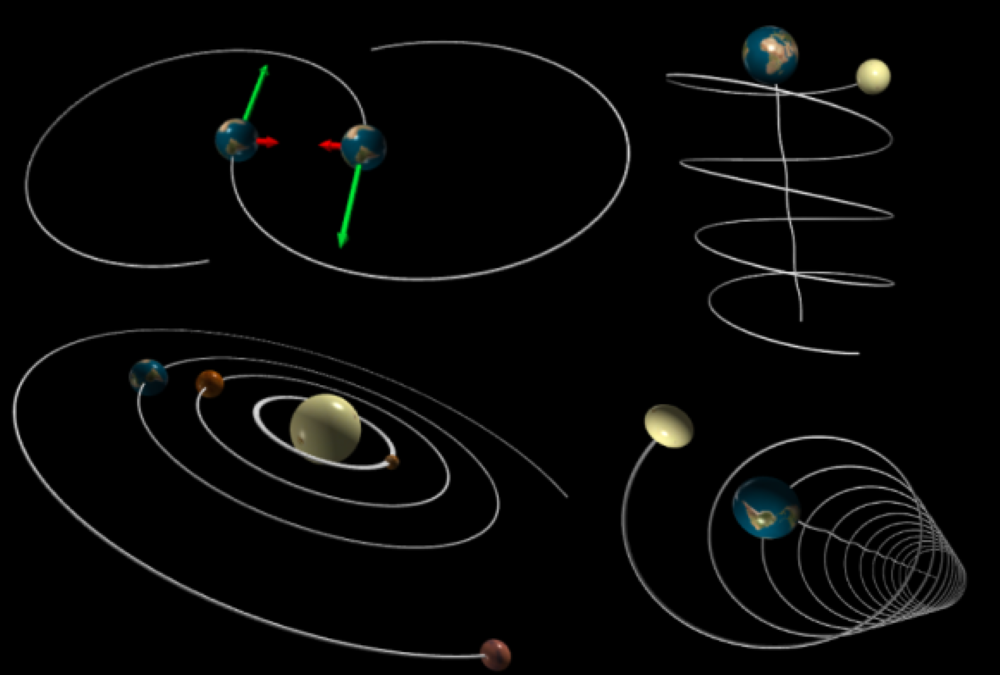
這是一個模擬行星互動的Python程序

這意味著您可以輸入行星質量，初始位置和速度，我們的程序將向您展示他們將如何通過一個不錯的模擬與彼此互動

我們的程序將向您顯示預期的情況，但可能不准確100％。

有很多現成的演示可能會給您留下深刻的印象！

特徵

您可以使用我們的應用程序可以做的一些事情：

與任何行星穆伯一起進入新的演示
保存演示再次使用它
在模擬過程中保存狀態以查看值詳細信息
暫停並恢復演示
重新啟動演示
擴展時間（使其較慢或更快）（較慢更準確）
添加行星的顏色和紋理（可選屬性）
在行星移動之後顯示步道（您還可以在亂七八糟的時候清除小徑）
顯示速度和加速箭頭（力）

技術堆棧

入門

先決條件

確保您已經在開發機上安裝了以下所有先決條件：

git-下載並安裝git。 OSX和Linux機器通常已經安裝了此功能。
Python-下載並安裝Python
PIP-安裝Python後，您將自動安裝PIP，您可以通過
```
 pip --version
```

安裝

首先在要下載項目的地方打開CMD，然後編寫此命令：

將存儲庫克隆到您的本地計算機：

 git clone https://github.com/suliman-99/Space-Simulation.git

導航到項目目錄：
```
 cd Space-Simulation
```
然後通過PIP安裝PipEnv模塊，只需在CMD上寫下此命令
```
 pip install pipenv
```
使用Pipenv安裝所需的依賴項：
```
 pipenv install
```
運行項目：
- 視窗：
```
 python main.py
```
- Linux或Mac：
```
 python3 main.py
```

用法

第一步是按照上一節安裝來運行程序。

應用按鈕將打開應用程序：單擊Create new Simulation以進行新的模擬或Simulation From File以打開現成的演示或打開保存的演示或狀態

然後單擊Run Simulation以啟動模擬

您的默認瀏覽器將在模擬頁面上打開

您可以通過單擊Save State按鈕來保存當前狀態，並將其保存在demos/saved_state.txt文件中，您可以從那裡再次使用它

如果您想嘗試一個新的演示，我很遺憾地說您需要關閉程序並再次打開程序

解釋

牛頓普遍重力定律

 F = (G * m1 * m2) / r^2

G ：引力常數

m1 ， m2 ：這兩個對象的質量

r ：質量中心之間的距離

F ：引力作用

我們使用此公式來計算每對行星之間的力

我們通過這種方法更新了Planeets的總力量：

 def apply_gravity(planet1: Planet, planet2: Planet) -> None:
     u = planet2.pos - planet1.pos
     grav = g * planet1.mass * planet2.mass / (u.length() ** 2)
     planet1.add_force(u.scale_to(grav))
     planet2.add_force(u.scale_to(-grav))

牛頓的第二項運動定律
F = m * a => a = F / m
m ：物體的質量
F ：全力施加
a ：加速度
我們使用此Fomula來計算每個行星的加速度，具體取決於施加的總力
之後，我們可以根據當前速度和加速度計算新速度（速度向量）
之後，我們可以根據當前位置和速度來計算新位置（x，y，z）
然後我們可以在新地方重新渲染對象
我們可以在同一秒（更多的10次）中做很多時間，我們將具有良好的可視化
我們通過此方法更新Palnet數據：
```
 def update(self, dt: float) -> None:
     self.pos += (self.velocity * dt) + (self.acceleration * ((dt ** 2) / 2))
     self.velocity += self.acceleration * dt
     self.acceleration = self.force / self.mass
```

另一個主題碰撞

項目構成

 Project Name
│   main.py
└───core
│   │   camera.py
│   │   environment.py
│   │   file.py
│   │   physics.py
│   │   planet.py
│   │   vector.py
│   
└───gui
    │   screens
    │   app.py
    │   controls.py