查看演示·报告错误·请求功能
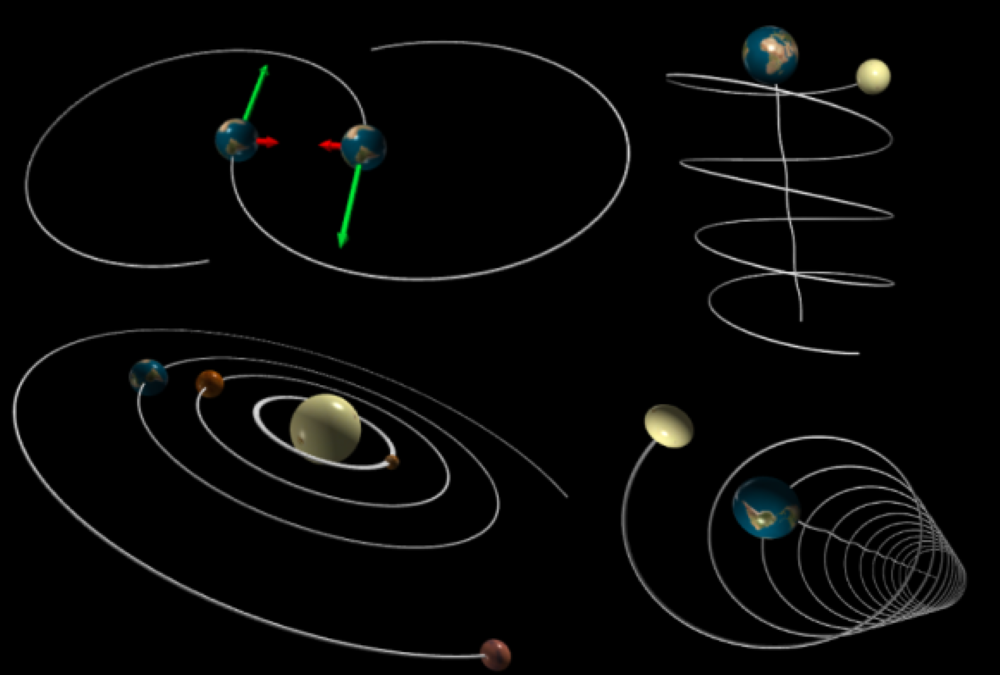
这是一个模拟行星互动的Python程序
这意味着您可以输入行星质量,初始位置和速度,我们的程序将向您展示他们将如何通过一个不错的模拟与彼此互动
我们的程序将向您显示预期的情况,但可能不准确100%。
有很多现成的演示可能会给您留下深刻的印象!
您可以使用我们的应用程序可以做的一些事情:
确保您已经在开发机上安装了以下所有先决条件:
pip --version
首先在要下载项目的地方打开CMD,然后编写此命令:
将存储库克隆到您的本地计算机:
git clone https://github.com/suliman-99/Space-Simulation.git
导航到项目目录:
cd Space-Simulation
然后通过PIP安装PipEnv模块,只需在CMD上写下此命令
pip install pipenv
使用Pipenv安装所需的依赖项:
pipenv install
运行项目:
视窗:
python main.py
Linux或Mac:
python3 main.py
第一步是按照上一节安装来运行程序。
应用按钮将打开应用程序:单击Create new Simulation以进行新的模拟或Simulation From File以打开现成的演示或打开保存的演示或状态
然后单击Run Simulation以启动模拟
您的默认浏览器将在模拟页面上打开
您可以通过单击Save State按钮来保存当前状态,并将其保存在demos/saved_state.txt文件中,您可以从那里再次使用它
如果您想尝试一个新的演示,我很遗憾地说您需要关闭程序并再次打开程序
牛顿普遍重力定律
F = (G * m1 * m2) / r^2
G :引力常数
m1 , m2 :这两个对象的质量
r :质量中心之间的距离
F :引力作用
我们使用此公式来计算每对行星之间的力
我们通过这种方法更新了Planeets的总力量:
def apply_gravity(planet1: Planet, planet2: Planet) -> None:
u = planet2.pos - planet1.pos
grav = g * planet1.mass * planet2.mass / (u.length() ** 2)
planet1.add_force(u.scale_to(grav))
planet2.add_force(u.scale_to(-grav))
牛顿的第二项运动定律
F = m * a => a = F / m
m :物体的质量
F :全力施加
a :加速度
我们使用此Fomula来计算每个行星的加速度,具体取决于施加的总力
之后,我们可以根据当前速度和加速度计算新速度(速度向量)
之后,我们可以根据当前位置和速度来计算新位置(x,y,z)
然后我们可以在新地方重新渲染对象
我们可以在同一秒(更多的10次)中做很多时间,我们将具有良好的可视化
我们通过此方法更新Palnet数据:
def update(self, dt: float) -> None:
self.pos += (self.velocity * dt) + (self.acceleration * ((dt ** 2) / 2))
self.velocity += self.acceleration * dt
self.acceleration = self.force / self.mass
另一个主题碰撞
Project Name
│ main.py
└───core
│ │ camera.py
│ │ environment.py
│ │ file.py
│ │ physics.py
│ │ planet.py
│ │ vector.py
│
└───gui
│ screens
│ app.py
│ controls.py
assets这是我们的图像demos是我们的演示,状态被保存为文件resources在这里一些顽固的全局变量testing这是我们的测试文件夹如果您对如何改善空间模拟或想报告错误的建议,请打开问题!我们希望所有的贡献。
有关更多信息,请查看贡献指南。
Suliman Awad [email protected] LinkedIn
项目链接:https://github.com/suliman-99/space-simulation
麻省理工学院许可证
版权(C)2023 Suliman Awad
有关更多信息,请查看许可证文件。