Demo anzeigen · Fehler melden · Anforderungsfunktion
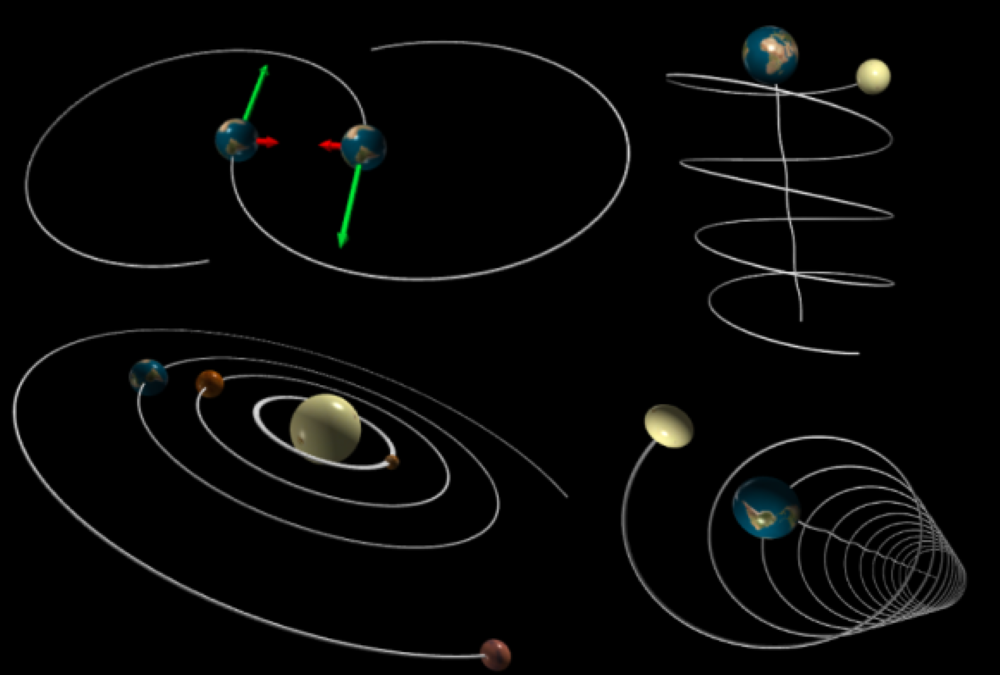
Dies ist ein Python -Programm zum Simulieren von Planeten -Interaktionen
Dies bedeutet, dass Sie die Planetenmassen und anfängliche Positionen und Geschwindigkeiten betreten können, und unser Programm zeigt Ihnen, wie sie in einer netten Simulation mit jedem interagieren würden
Unser Programm zeigt Ihnen ein erwartetes Szenario, ist jedoch möglicherweise nicht 100% genau.
Es gibt viele fertige Demos, die Sie beeindrucken können!
Einige der Dinge, die Sie mit unserer App machen können:
Stellen Sie sicher, dass Sie alle folgenden Voraussetzungen auf Ihrer Entwicklungsmaschine installiert haben:
pip --version
Öffnen Sie zuerst CMD an dem Ort, an dem Sie das Projekt herunterladen möchten, und schreiben Sie dann diese Befehle:
Klonen Sie das Repository in Ihre lokale Maschine:
git clone https://github.com/suliman-99/Space-Simulation.git
Navigieren Sie zum Projektverzeichnis:
cd Space-Simulation
Dann schreiben
pip install pipenv
Installieren Sie die erforderlichen Abhängigkeiten mit Pipenv:
pipenv install
Führen Sie das Projekt aus:
Fenster:
python main.py
Linux oder Mac:
python3 main.py
Der erste Schritt besteht darin, das Programm durch Befolgen der vorherigen Abschnitt -Installation auszuführen.
Eine App wird mit Schlepptasten geöffnet: Klicken Sie auf Create new Simulation um eine neue zu erstellen, oder wählen Sie Simulation From File Dateischaltfläche, um eine vorgefertigte Demo zu öffnen, oder um Ihre gespeicherten Demos oder Zustände zu öffnen
Klicken Sie dann Run Simulation , um die Simulation zu starten
Ihr Standardbrowser wird mit der Simulationsseite geöffnet
Sie können den aktuellen Status speichern, indem Sie auf die demos/saved_state.txt Save State speichern.
Wenn Sie eine neue Demo ausprobieren möchten, sagen Sie, Sie müssen das Programm schließen und erneut öffnen
Newtons Gesetz der universellen Gravitation
F = (G * m1 * m2) / r^2
G : Die Gravitationskonstante
m1 , m2 : Die Massen dieser beiden Objekte
r : Der Abstand zwischen den Zentren der Massen
F : Die Gravitationskraft, die zwischen ihnen wirkt
Wir verwenden diese Formel, um die Kraft zu berechnen, die zwischen jedem Planetenpaar
Wir aktualisieren die Gesamtkraft für Planeets mit dieser Methode:
def apply_gravity(planet1: Planet, planet2: Planet) -> None:
u = planet2.pos - planet1.pos
grav = g * planet1.mass * planet2.mass / (u.length() ** 2)
planet1.add_force(u.scale_to(grav))
planet2.add_force(u.scale_to(-grav))
Newtons zweites Bewegungsgesetz
F = m * a => a = F / m
m : Masse des Objekts
F : Auf sie angewendete Gesamtkraft
a : Die Beschleunigung davon
Wir verwenden diese Fomula, um die Beschleunigung jedes Planeten je nach der gesamten aufgebrachten Gesamtkraft zu berechnen
Danach können wir die neue Geschwindigkeit (Geschwindigkeitsvektor) je nach Stromgeschwindigkeit und Beschleunigung berechnen
Danach können wir die neue Position (x, y, z) je nach aktueller Position und Geschwindigkeit berechnen
Dann können wir das Objekt an dem neuen Ort erneut rendern
Wir können das viel Zeit in derselben Sekundie (mehr als 10 Mal) und wir werden eine gute Visualisierung haben
Wir aktualisieren die Palnet -Daten mit dieser Methode:
def update(self, dt: float) -> None:
self.pos += (self.velocity * dt) + (self.acceleration * ((dt ** 2) / 2))
self.velocity += self.acceleration * dt
self.acceleration = self.force / self.mass
Ein weiteres Thema Kollision
Project Name
│ main.py
└───core
│ │ camera.py
│ │ environment.py
│ │ file.py
│ │ physics.py
│ │ planet.py
│ │ vector.py
│
└───gui
│ screens
│ app.py
│ controls.py
assets hier sind unsere Bilderdemos hier sind unsere Demos und Staaten werden als Dateien gespeichertresources hier einige Stubid Global Variablentesting Dies ist unser Testordner Wenn Sie Vorschläge für die Verbesserung der Raumsimulation haben oder einen Fehler melden möchten, öffnen Sie ein Problem! Wir würden alle und alle Beiträge lieben.
Weitere Informationen finden Sie im beitragenden Leitfaden.
Suliman awad - [email protected] - linkedIn
Projektlink: https://github.com/suliman-99/space-simulation
MIT -Lizenz
Copyright (C) 2023 Suliman Awad
Weitere Informationen finden Sie in der Lizenzdatei.