Download Space Simulation - Space Simulation Download do código -fonte

Space Simulation

Outro código-fonte

1.0.0

Baixar

Simulação espacial

Visualizar demonstração · Relatório Bug · Solicitar recurso

foto

Índice

Introdução
Características
Pilha de tecnologia
Começando
- Pré -requisitos
- Instalação
- Uso
Explicação
Estrutura do projeto
Contribuindo
Contato
Companheiros de equipe
Licença

Introdução

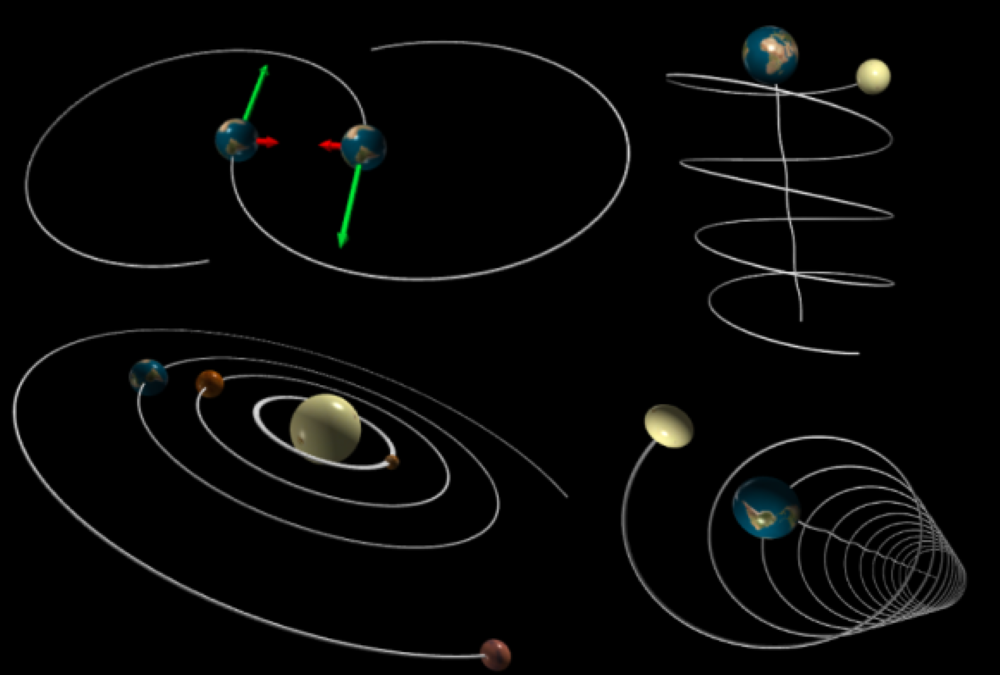
Este é um programa Python para simular as interações dos planetas

Isso significa que você pode entrar nas massas dos planetas e posições e velocidades iniciais e nosso programa mostrará como eles interagiriam com um dos um a um bom simulação

Nosso programa mostrará um cenário esperado, mas pode não ser 100% preciso.

Existem muitas demos prontas podem impressioná-lo!

Características

Algumas das coisas que você pode fazer com nosso aplicativo:

Digite uma nova demonstração com qualquer muber de planetas
Salve uma demonstração para usá -la novamente
Salvar um estado durante a simulação para ver os detalhes dos valores
Pausar e retomar a demonstração
Reinicie a demonstração
Escala o tempo (torne -o mais lento ou mais rápido) (mais lento é mais preciso)
Adicione cores e texturas para planetas (atributo opcional)
Mostre trilhas seguindo os movimentos dos planetas (você também pode limpar as trilhas quando elas fazem uma bagunça)
Mostre as setas de velocidade e aceleração (forças)

Pilha de tecnologia

Começando

Pré -requisitos

Certifique -se de instalar todos os seguintes pré -requisitos em sua máquina de desenvolvimento:

Git - Download e instale o git. As máquinas OSX e Linux normalmente já estão instaladas.
Python - Baixar e instalar Python
PIP - Depois de instalar o Python, você terá o Pip instalado em seu Machin automaticamente, você pode verificar por
```
 pip --version
```

Instalação

Primeiro Open CMD no local em que você deseja baixar o projeto e, em seguida, escreva os comandos:

Clone o repositório da sua máquina local:

 git clone https://github.com/suliman-99/Space-Simulation.git

Navegue até o diretório do projeto:
```
 cd Space-Simulation
```
Então, para instalar o módulo PIPENV por PIP, basta escrever este comando em seu CMD
```
 pip install pipenv
```
Instale as dependências necessárias usando PIPENV:
```
 pipenv install
```
Execute o projeto:
- Windows:
```
 python main.py
```
- Linux ou Mac:
```
 python3 main.py
```

Uso

A primeira etapa é executar o programa seguindo a instalação da seção anterior.

Um aplicativo será aberto com botões de reboque: clique em Create new Simulation para fazer um novo ou escolher Simulation From File para abrir uma demonstração pronta ou para abrir suas demos ou estados salvos

Em seguida, clique em Run Simulation para iniciar a simulação

Seu navegador padrão abrirá com a página de simulação

Você pode salvar o estado atual clicando no botão Save State e ele será salvo no arquivo demos/saved_state.txt , e você poderá usá -lo novamente a partir daí

Se você quiser experimentar uma nova demonstração, lamento dizer que você precisa fechar o programa e abri -lo novamente

Explicação

Lei de Gravitação Universal de Newton
```
 F = (G * m1 * m2) / r^2
```
G : a constante gravitacional
m1 , m2 : As massas desses dois objetos
r : A distância entre os centros das massas
F : A força gravitacional que atua entre eles
Usamos esta fórmula para calcular a força entre cada par de planetas
Atualizamos a força total para as aviões por este método:
```
 def apply_gravity(planet1: Planet, planet2: Planet) -> None:
     u = planet2.pos - planet1.pos
     grav = g * planet1.mass * planet2.mass / (u.length() ** 2)
     planet1.add_force(u.scale_to(grav))
     planet2.add_force(u.scale_to(-grav))
```
Segunda Lei do Movimento de Newton
F = m * a => a = F / m
m : Massa do objeto
F : Força total aplicada nele
a : A aceleração disso
Usamos essa fomula para calcular a aceleração de cada planeta, dependendo da força total aplicada nela
Depois disso, podemos calcular a nova velocidade (vetor de velocidade), dependendo da velocidade atual e da aceleração
Depois disso, podemos calcular a nova posição (x, y, z), dependendo da posição atual e da velocidade
então podemos renderizar o objeto no novo lugar
Podemos fazer isso muito tempo no mesmo segundo (mais da que 10 vezes) e teremos uma boa visualização
Atualizamos os dados do PALNET por este método:
```
 def update(self, dt: float) -> None:
     self.pos += (self.velocity * dt) + (self.acceleration * ((dt ** 2) / 2))
     self.velocity += self.acceleration * dt
     self.acceleration = self.force / self.mass
```

Outra colisão do tópico

Estrutura do projeto

 Project Name
│   main.py
└───core
│   │   camera.py
│   │   environment.py
│   │   file.py
│   │   physics.py
│   │   planet.py
│   │   vector.py
│   
└───gui
    │   screens
    │   app.py
    │   controls.py

assets aqui estão nossas imagens
demos aqui estão nossas demos e os estados são salvos como arquivos
resources aqui algumas variáveis globais estúbas
testing esta é a nossa pasta de teste

Contribuindo

Se você tiver sugestões de como a simulação espacial pode ser melhorada ou deseja relatar um bug, abra um problema! Adoraríamos todas e quaisquer contribuições.

Para mais informações, confira o guia contribuinte.