ดาวน์โหลด Space Simulation - ดาวน์โหลดซอร์สโค้ด Space Simulation

Space Simulation

ซอร์สโค้ดอื่น ๆ

1.0.0

ดาวน์โหลด

การกลั่นกรองอวกาศ

ดูการสาธิต·รายงานข้อบกพร่อง·คุณลักษณะการร้องขอ

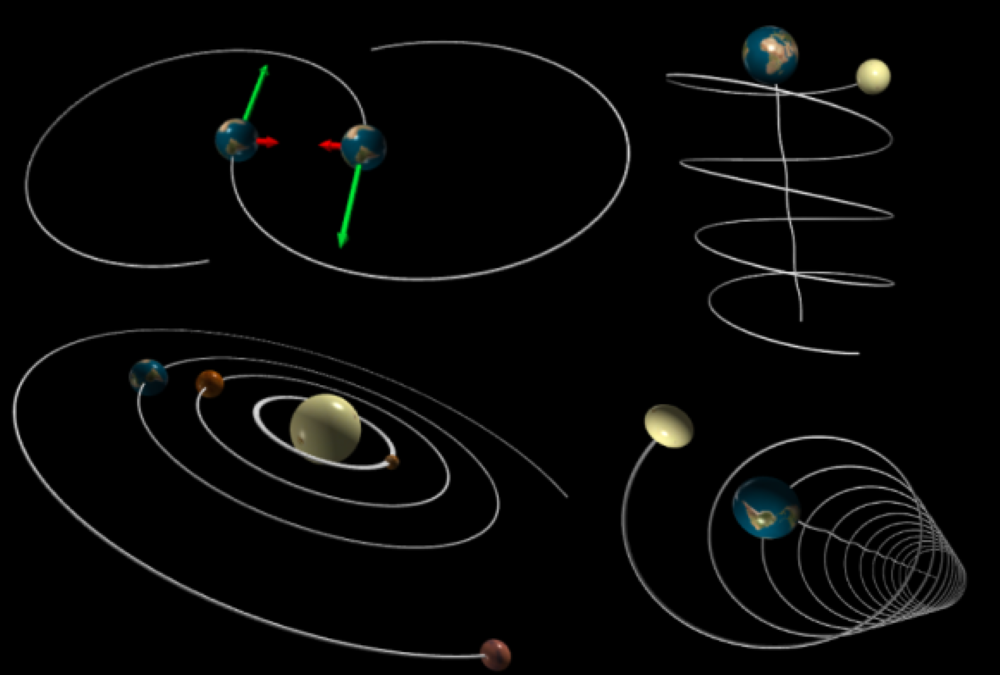
รูปถ่าย

สารบัญ

การแนะนำ
คุณสมบัติ
ซ้อนเทค
เริ่มต้น
- ข้อกำหนดเบื้องต้น
- การติดตั้ง
- การใช้งาน
คำอธิบาย
โครงสร้างของโครงการ
การบริจาค
ติดต่อ
เพื่อนร่วมทีม
ใบอนุญาต

การแนะนำ

นี่คือโปรแกรม Python เพื่อจำลองการโต้ตอบของดาวเคราะห์

หมายความว่าคุณสามารถเข้าสู่มวลดาวเคราะห์และตำแหน่งเริ่มต้นและความเร็วและโปรแกรมของเราจะแสดงให้คุณเห็นว่าพวกเขาจะโต้ตอบกับแต่ละคนในการจำลองที่ดีได้อย่างไร

โปรแกรมของเราจะแสดงสถานการณ์ที่คาดหวังให้คุณ แต่อาจไม่แม่นยำ 100%

มีการสาธิตสำเร็จรูปมากมายอาจทำให้คุณประทับใจ!

คุณสมบัติ

บางสิ่งที่คุณสามารถทำได้กับแอพของเรา:

ป้อนการสาธิตใหม่กับ Muber of Planets ใด ๆ
บันทึกการสาธิตเพื่อใช้อีกครั้ง
บันทึกสถานะระหว่างการจำลองเพื่อดูรายละเอียดค่า
หยุดชั่วคราวและกลับมาสาธิต
รีสตาร์ทการสาธิต
ปรับขนาดเวลา (ทำให้ช้าลงหรือเร็วขึ้น) (ช้ากว่านั้นแม่นยำกว่า)
เพิ่มสีและพื้นผิวสำหรับดาวเคราะห์ (แอตทริบิวต์เสริม)
แสดงเส้นทางหลังจากการเคลื่อนที่ของดาวเคราะห์ (คุณสามารถล้างเส้นทางเมื่อพวกเขาทำยุ่งเหยิง)
แสดงความเร็วและความเร่งลูกศร (กองกำลัง)

ซ้อนเทค

เริ่มต้น

ข้อกำหนดเบื้องต้น

ตรวจสอบให้แน่ใจว่าคุณได้ติดตั้งข้อกำหนดเบื้องต้นทั้งหมดต่อไปนี้ในเครื่องพัฒนาของคุณ:

Git - ดาวน์โหลดและติดตั้ง Git โดยทั่วไปแล้วเครื่อง OSX และ Linux จะติดตั้งแล้ว
Python - ดาวน์โหลดและติดตั้ง Python
PIP - หลังจากติดตั้ง Python แล้วคุณจะติดตั้ง PIP บน machin ของคุณโดยอัตโนมัติคุณสามารถตรวจสอบได้
```
 pip --version
```

การติดตั้ง

เปิด CMD ครั้งแรกในสถานที่ที่คุณต้องการดาวน์โหลดโครงการแล้วเขียนคำสั่งนี้:

โคลนที่เก็บไปยังเครื่องในพื้นที่ของคุณ:
```
 git clone https://github.com/suliman-99/Space-Simulation.git
```
นำทางไปยังไดเรกทอรีโครงการ:
```
 cd Space-Simulation
```
จากนั้นในการติดตั้งโมดูล pipenv โดย PIP เพียงแค่เขียนคำสั่งนี้บน cmd ของคุณ
```
 pip install pipenv
```
ติดตั้งการพึ่งพาที่ต้องการโดยใช้ PIPENV:
```
 pipenv install
```
เรียกใช้โครงการ:
- Windows:
```
 python main.py
```
- Linux หรือ Mac:
```
 python3 main.py
```

การใช้งาน

ขั้นตอนแรกคือการเรียกใช้โปรแกรมโดยติดตามการติดตั้งส่วนก่อนหน้า

แอพจะเปิดด้วยปุ่มพ่วง: คลิก Create new Simulation เพื่อสร้างใหม่หรือเลือก Simulation From File เพื่อเปิดการสาธิตสำเร็จรูปหรือเพื่อเปิดการสาธิตหรือสถานะที่บันทึกไว้ของคุณ

จากนั้นคลิกเรียก Run Simulation เพื่อเริ่มการจำลอง

เบราว์เซอร์เริ่มต้นของคุณจะเปิดพร้อมหน้าการจำลอง

คุณสามารถบันทึกสถานะปัจจุบันได้โดยคลิกที่ปุ่ม Save State และจะถูกบันทึกไว้ในไฟล์ demos/saved_state.txt และคุณสามารถใช้อีกครั้งจากที่นั่น

หากคุณต้องการลองตัวอย่างใหม่ฉันขอโทษที่ต้องบอกว่าคุณต้องปิดโปรแกรมและเปิดอีกครั้ง

คำอธิบาย

กฎของความโน้มถ่วงสากลของนิวตัน
```
 F = (G * m1 * m2) / r^2
```
G : ค่าคงที่แรงโน้มถ่วง
m1 , m2 : มวลของวัตถุทั้งสองนี้
r : ระยะห่างระหว่างศูนย์กลางของมวลชน
F : แรงโน้มถ่วงที่ทำหน้าที่ระหว่างพวกเขา
เราใช้สูตรนี้เพื่อคำนวณแรงหนุนระหว่างดาวเคราะห์แต่ละคู่
เราอัปเดตแรงทั้งหมดสำหรับ Planeets ด้วยวิธีนี้:
```
 def apply_gravity(planet1: Planet, planet2: Planet) -> None:
     u = planet2.pos - planet1.pos
     grav = g * planet1.mass * planet2.mass / (u.length() ** 2)
     planet1.add_force(u.scale_to(grav))
     planet2.add_force(u.scale_to(-grav))
```
กฎข้อที่สองของนิวตัน
F = m * a => a = F / m
m : มวลของวัตถุ
F : แรงทั้งหมดใช้กับมัน
a : การเร่งความเร็วของมัน
เราใช้ fomula นี้เพื่อคำนวณการเร่งความเร็วของดาวเคราะห์แต่ละดวงขึ้นอยู่กับแรงทั้งหมดที่ใช้กับมัน
หลังจากนั้นเราสามารถคำนวณความเร็วใหม่ (เวกเตอร์ความเร็ว) ขึ้นอยู่กับความเร็วปัจจุบันและการเร่งความเร็ว
หลังจากนั้นเราสามารถคำนวณตำแหน่งใหม่ (x, y, z) ขึ้นอยู่กับตำแหน่งปัจจุบันและความเร็ว
จากนั้นเราสามารถแสดงวัตถุใหม่ในสถานที่ใหม่ได้
เราสามารถทำเช่นนั้นได้มากในวินาทีเดียวกัน (มากกว่า 10 ครั้ง) และเราจะมีการสร้างภาพที่ดี
เราอัปเดตข้อมูล Palnet ด้วยวิธีนี้:
```
 def update(self, dt: float) -> None:
     self.pos += (self.velocity * dt) + (self.acceleration * ((dt ** 2) / 2))
     self.velocity += self.acceleration * dt
     self.acceleration = self.force / self.mass
```

การชนหัวข้ออื่น

โครงสร้างของโครงการ

 Project Name
│   main.py
└───core
│   │   camera.py
│   │   environment.py
│   │   file.py
│   │   physics.py
│   │   planet.py
│   │   vector.py
│   
└───gui
    │   screens
    │   app.py
    │   controls.py