Descarga Space Simulation - Descargar código fuente Space Simulation

Space Simulation

Otro código fuente

1.0.0

Descargar

Simulación de espacio

Ver demostración · Informe de error · Función de solicitud

foto

Tabla de contenido

Introducción
Características
Pila de tecnología
Empezando
- Requisitos previos
- Instalación
- Uso
Explicación
Estuctura del proyecto
Que contribuye
Contacto
Compañeros de equipo
Licencia

Introducción

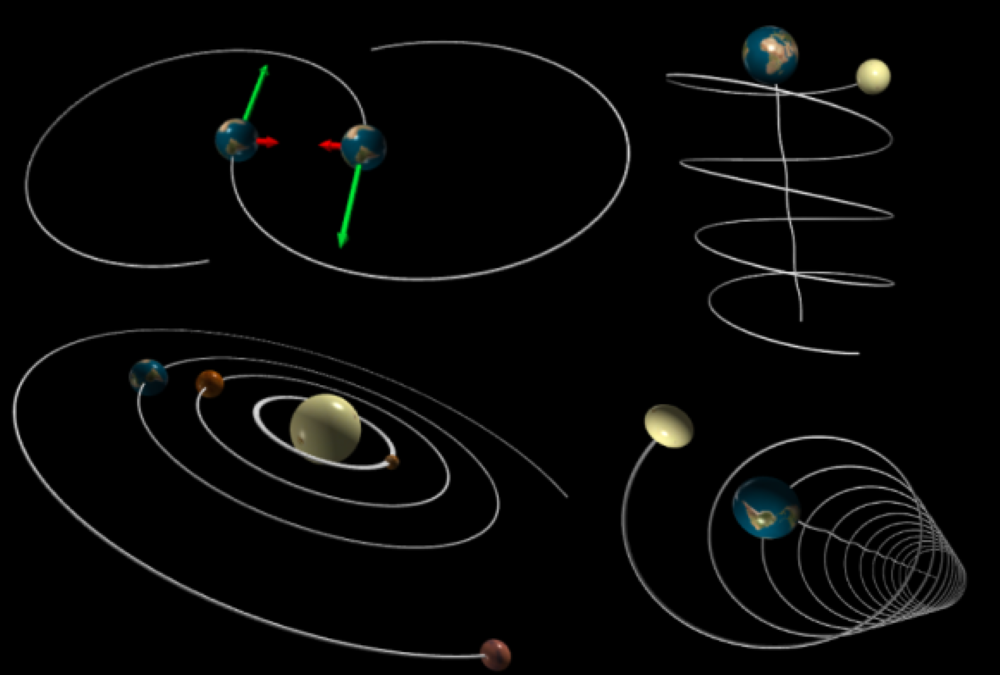
Este es un programa de Python para simular las interacciones de los planetas

Significa que puede ingresar a las masas de los planetas y las posiciones y velocidades iniciales y nuestro programa le mostrará cómo interactuarían con los demás en una buena simulación.

Nuestro programa le mostrará un escenario esperado, pero puede que no sea 100% preciso.

¡Hay muchas demostraciones preparadas para impresionarlo!

Características

Algunas de las cosas que puedes hacer con nuestra aplicación:

Ingrese una nueva demostración con cualquier tumbon de planetas
Guarde una demostración para usarlo nuevamente
Guardar un estado durante la simulación para ver los detalles de los valores
Pausa y reanude la demostración
Reiniciar la demostración
Escala el tiempo (hacerlo más lento o más rápido) (más lento es más preciso)
Agregar colores y texturas para planetas (atributo opcional)
Show Trails siguiendo los movimientos de los planetas (también puedes limpiar los senderos cuando hacen un desastre)
Mostrar las flechas de velocidad y aceleración (fuerzas)

Pila de tecnología

Empezando

Requisitos previos

Asegúrese de haber instalado todos los siguientes requisitos previos en su máquina de desarrollo:

Git - Descargar e instalar Git. Las máquinas OSX y Linux generalmente tienen esto ya instalado.
Python - Descargar e instalar Python
PIP: después de instalar Python, tendrá instalado PIP en su Machin automáticamente, puede verificarlo
```
 pip --version
```

Instalación

Primero abra CMD en el lugar en el que desea descargar el proyecto y luego escriba estos comandos:

Clonar el repositorio de su máquina local:

 git clone https://github.com/suliman-99/Space-Simulation.git

Navegue al directorio del proyecto:
```
 cd Space-Simulation
```
Luego, para instalar el módulo PIPENV por PIP, simplemente escriba este comando en su CMD
```
 pip install pipenv
```
Instale las dependencias requeridas usando Pipenv:
```
 pipenv install
```
Ejecute el proyecto:
- Windows:
```
 python main.py
```
- Linux o Mac:
```
 python3 main.py
```

Uso

El primer paso es ejecutar el programa siguiendo la instalación de la sección anterior.

Una aplicación se abrirá con botones de remolque: haga clic en Create new Simulation para hacer una nueva o elegir Simulation From File para abrir una demostración preparada o para abrir sus demostraciones o estados guardados

Luego haga clic Run Simulation para iniciar la simulación

Su navegador predeterminado se abrirá con la página de simulación

Puede guardar el estado actual haciendo clic en el botón Save State y se guardará en el archivo demos/saved_state.txt , y puede usarlo nuevamente desde allí

Si quieres probar una nueva demostración, lamento decir que necesitas cerrar el programa y abrirlo de nuevo.

Explicación

Ley de gravitación universal de Newton
```
 F = (G * m1 * m2) / r^2
```
G : La constante gravitacional
m1 , m2 : las masas de estos dos objetos
r : La distancia entre los centros de las masas
F : La fuerza gravitacional que actúa entre ellos
Usamos esta fórmula para calcular la fuerza entre cada par de planetas
Actualizamos la fuerza total para planeets por este método:
```
 def apply_gravity(planet1: Planet, planet2: Planet) -> None:
     u = planet2.pos - planet1.pos
     grav = g * planet1.mass * planet2.mass / (u.length() ** 2)
     planet1.add_force(u.scale_to(grav))
     planet2.add_force(u.scale_to(-grav))
```
La segunda ley de movimiento de Newton
F = m * a => a = F / m
m : Misa del objeto
F : Fuerza total aplicada sobre él
a : la aceleración de la misma
Utilizamos esta fomula para calcular la aceleración de cada planeta dependiendo de la fuerza total aplicada en él
Después de eso, podemos calcular la nueva velocidad (vector de velocidad) dependiendo de la velocidad actual y la aceleración
Después de eso, podemos calcular la nueva posición (x, y, z) dependiendo de la posición actual y la velocidad
Entonces podemos volver a renderizar el objeto en el nuevo lugar
Podemos hacerlo mucho tiempo en el mismo segundo (más esa 10 veces) y tendremos una buena visualización
Actualizamos los datos de Palnet mediante este método:
```
 def update(self, dt: float) -> None:
     self.pos += (self.velocity * dt) + (self.acceleration * ((dt ** 2) / 2))
     self.velocity += self.acceleration * dt
     self.acceleration = self.force / self.mass
```

Otro tema de colisión

Estuctura del proyecto

 Project Name
│   main.py
└───core
│   │   camera.py
│   │   environment.py
│   │   file.py
│   │   physics.py
│   │   planet.py
│   │   vector.py
│   
└───gui
    │   screens
    │   app.py
    │   controls.py

assets Aquí están nuestras imágenes
demos aquí son nuestras demostraciones y los estados se guardan como archivos
resources aquí algunas variables globales estómicas
testing esta es nuestra carpeta de prueba

Que contribuye

Si tiene sugerencias sobre cómo se podría mejorar la simulación de espacio, o desea informar un error, ¡abra un problema! Nos encantaría todos y cualquier contribución.

Para obtener más información, consulte la guía contribuyente.