Space Simulation Download - Space Simulation Source code download

Space Simulation

Other source code

1.0.0

Download

Space-Simulation

View Demo · Report Bug · Request Feature

Introduction

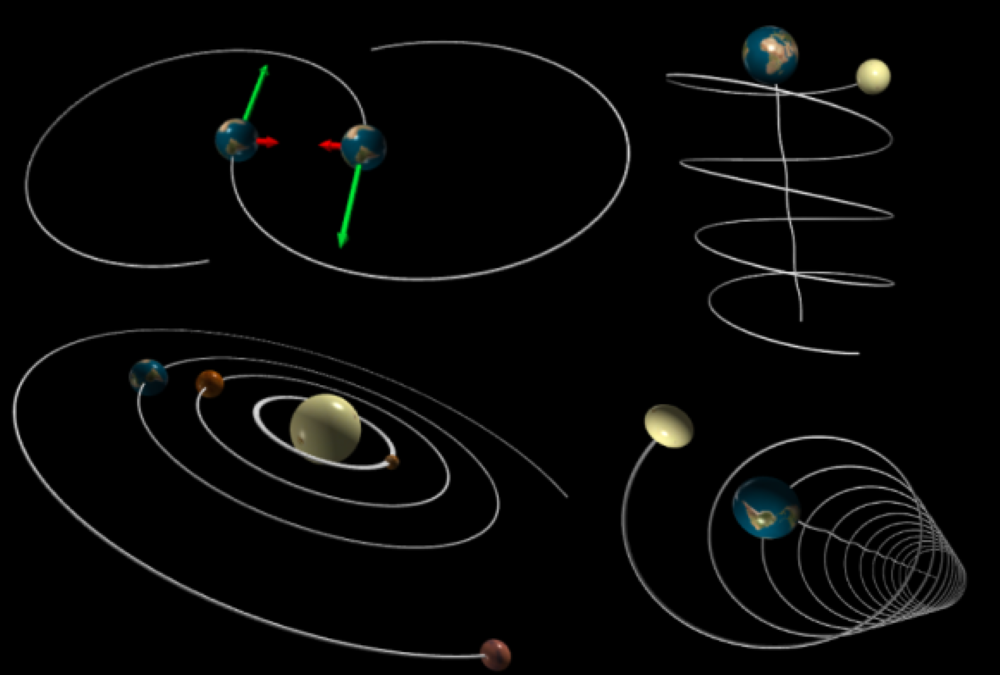
This is a Python program to simulate planets interactions

It means that you can enter the planets masses and initial positions and velocities and our program will show you how would they interact with eachothers in a nice simulation

our program will show you an expected scenario but It may not be 100% accurate.

There are many ready-made demos may impress you !

Features

A few of the things you can do with our app:

Enter a new demo with any muber of planets
Save a demo to use it again
Save a state during the simulation to see the values details
Pause and resume the demo
Restart the demo
Scale the time (make it slower or faster) (slower is more accurate)
Add colors and textures for planets (Optional attribute)
Show trails following the planets moves (You can also clear the Trails when they make a mess)
Show the velocity and acceleration Arrows (Forces)

Tech Stack

Getting Started

Prerequisites

Make sure you have installed all of the following prerequisites on your development machine:

Git - Download & Install Git. OSX and Linux machines typically have this already installed.
Python - Download & Install Python
pip - after you install python you will have pip installed on your machin automatically you can check it by
```
pip --version
```

Installation

first open cmd in the place you want to download the project in then write this commands :

Clone the repository to your local machine:

git clone https://github.com/suliman-99/Space-Simulation.git

Navigate to the project directory:
```
cd Space-Simulation
```
then to install pipenv module by pip just write this command on your cmd
```
pip install pipenv
```
Install the required dependencies using pipenv:
```
pipenv install
```
Run the project:
- Windows:
```
python main.py
```
- Linux or Mac:
```
python3 main.py
```

Usage

The first step is to run the program by following the previous section Installation.

An app will open with tow buttons: click Create new Simulation to make a new one or choose Simulation From File button to open a ready-made demo or to open your saved demos or states

then Click Run Simulation to start the simulation

your default browser will open with the simulation page

you can save the current state by clicking on Save State Button and it will be saved in the demos/saved_state.txt file, and you can use it again from there

If you want to try a new demo I am sorry to say that you need to close the program and open it again

Explanation

Newton's law of universal gravitation
```
F = (G * m1 * m2) / r^2
```
G: the gravitational constant

m1, m2: the masses of these two objects

r: the distance between the centers of the masses

F: the gravitational force acting between them

we use this Formula to calculate the force berween each pair of planets

We update the total force for planeets by this method:
```
 def apply_gravity(planet1: Planet, planet2: Planet) -> None:
     u = planet2.pos - planet1.pos
     grav = g * planet1.mass * planet2.mass / (u.length() ** 2)
     planet1.add_force(u.scale_to(grav))
     planet2.add_force(u.scale_to(-grav))
```
Newton's Second Law of Motion

F = m * a => a = F / m

m: mass of the object

F : Total Force applied on it

a: the acceleration of it

We Use this Fomula to calculate the acceleration of each planet depending on the total force applied on it

after that we can calculate the new velocity (speed vector) depending on the current velocity and the acceleration

after that we can calculate the new position (x, y, z) depending on the current position and the velocity

then we can re-render the object in the new place

we can do that a lot of time in the same seconde (more that 10 time) and we will have a good visualization

We update the palnet data by this method:
```
 def update(self, dt: float) -> None:
     self.pos += (self.velocity * dt) + (self.acceleration * ((dt ** 2) / 2))
     self.velocity += self.acceleration * dt
     self.acceleration = self.force / self.mass
```

Another Topic Collision

Project stucture

Project Name
│   main.py
└───core
│   │   camera.py
│   │   environment.py
│   │   file.py
│   │   physics.py
│   │   planet.py
│   │   vector.py
│   
└───gui
    │   screens
    │   app.py
    │   controls.py