Optimlib是非线性函数数值优化方法的轻量级C ++库。
特征:
float )或双精度( double )库可用。当前可用算法的列表包括:
完整的文档可在线提供:
该文档的PDF版本可在此处找到。
Optimlib API遵循相对简单的惯例,大多数算法以以下方式调用:
algorithm_id(<initial/final values>, <objective function>, <objective function data>);
输入按顺序为:
例如,使用BFGS算法使用
bfgs (ColVec_t& init_out_vals, std::function< double ( const ColVec_t& vals_inp, ColVec_t* grad_out, void * opt_data)> opt_objfn, void* opt_data); ColVec_t用于表示,例如,例如, arma::vec或Eigen::VectorXd类型。
Optimlib仅作为单与UNIX类型系统的编译共享库,或仅作为仅标题库(例如,流行的基于Linux的发行版以及MACOS)。不支持此库与基于Windows的系统使用或没有MSVC。
Optimlib需要armadillo或eigen C ++线性代数库。 (请注意,EIGEN版本3.4.0需要C ++ 14兼容的编译器。)
在包含标头文件之前,定义以下一个:
# define OPTIM_ENABLE_ARMA_WRAPPERS
# define OPTIM_ENABLE_EIGEN_WRAPPERS例子:
# define OPTIM_ENABLE_EIGEN_WRAPPERS
# include " optim.hpp "可以通过标准./configure && make方法安装库。
首先克隆图书馆和任何必要的子模型:
# clone optim into the current directory
git clone https://github.com/kthohr/optim ./optim
# change directory
cd ./optim
# clone necessary submodules
git submodule update --init在运行configure之前设置(一个)以下环境变量:
export ARMA_INCLUDE_PATH=/path/to/armadillo
export EIGEN_INCLUDE_PATH=/path/to/eigen最后:
# build and install with Eigen
./configure -i " /usr/local " -l eigen -p
make
make install最终命令将在/usr/local中安装OptimLib。
配置选项(请参阅./configure -h ):
基本的
-h打印帮助-i安装路径;默认值:构建目录-f浮点精度模式;默认值: double-l指定线性代数库的选择;选择arma或eigen-m指定要链接的Blas和Lapack库;例如, -m "-lopenblas"或-m "-framework Accelerate"-o编译器优化选项;默认为-O3 -march=native -ffp-contract=fast -flto -DARMA_NO_DEBUG-p启用OpenMP并行功能(建议)次要
-c覆盖范围构建(与Codecov一起使用)-d开发''构建-g调试构建(设置为-O0 -g优化标志)特别的
--header-only-version生成一个仅标题版本的Optimlib(见下文) Optimlib也可以作为仅标题库(即,无需编译共享库)提供。只需使用--header-only-version选项运行configure :
./configure --header-only-version这将创建一个新的目录header_only_version ,其中包含OptimLib的副本,并在内联工作中修改为工作。使用此仅标头版本,只需包含标头文件( #include "optim.hpp ),然后将Inclage路径设置为head_only_version目录(例如, -I/path/to/optimlib/header_only_version )。
要将Optimlib与R软件包一起使用,请首先生成库的仅标题版本(请参见上文)。然后,只需在包含OptimLib文件之前添加编译器定义。
# define OPTIM_USE_RCPP_ARMADILLO
# include " optim.hpp "# define OPTIM_USE_RCPP_EIGEN
# include " optim.hpp " 为了说明在工作中的Optimlib,请考虑搜索Ackley函数的全球最小值:
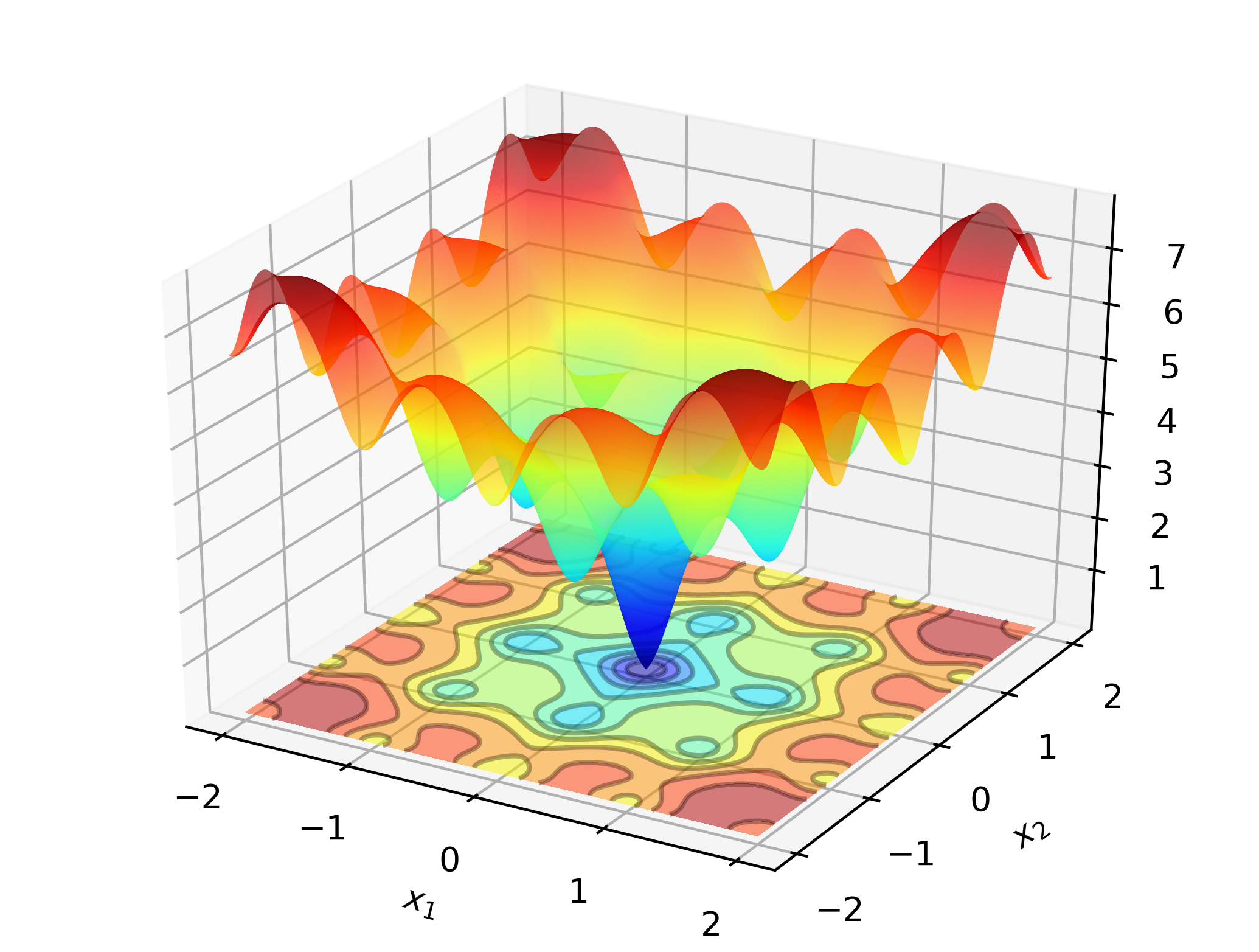
这是许多局部最小值的众所周知的测试功能。牛顿型方法(例如BFGS)对选择初始值的选择敏感,并且在这里表现较差。因此,我们将采用一种全球搜索方法 - 在这种情况下:差异进化。
代码:
# define OPTIM_ENABLE_EIGEN_WRAPPERS
# include " optim.hpp "
# define OPTIM_PI 3.14159265358979
double
ackley_fn ( const Eigen::VectorXd& vals_inp, Eigen::VectorXd* grad_out, void * opt_data)
{
const double x = vals_inp ( 0 );
const double y = vals_inp ( 1 );
const double obj_val = 20 + std::exp ( 1 ) - 20 * std::exp ( - 0.2 * std::sqrt ( 0.5 *(x*x + y*y)) ) - std::exp ( 0.5 *( std::cos ( 2 * OPTIM_PI * x) + std::cos ( 2 * OPTIM_PI * y)) );
return obj_val;
}
int main ()
{
Eigen::VectorXd x = 2.0 * Eigen::VectorXd::Ones ( 2 ); // initial values: (2,2)
bool success = optim::de (x, ackley_fn, nullptr );
if (success) {
std::cout << " de: Ackley test completed successfully. " << std::endl;
} else {
std::cout << " de: Ackley test completed unsuccessfully. " << std::endl;
}
std::cout << " de: solution to Ackley test: n " << x << std::endl;
return 0 ;
}在基于X86的计算机上,可以使用以下方式编译此示例:
g++ -Wall -std=c++14 -O3 -march=native -ffp-contract=fast -I/path/to/eigen -I/path/to/optim/include optim_de_ex.cpp -o optim_de_ex.out -L/path/to/optim/lib -loptim输出:
de: Ackley test completed successfully.
elapsed time: 0.028167s
de: solution to Ackley test:
-1.2702e-17
-3.8432e-16
在标准笔记本电脑上,Optimlib将在一秒钟内计算到机器精度内的解决方案。
此示例的基于Armadillo的版本:
# define OPTIM_ENABLE_ARMA_WRAPPERS
# include " optim.hpp "
# define OPTIM_PI 3.14159265358979
double
ackley_fn ( const arma::vec& vals_inp, arma::vec* grad_out, void * opt_data)
{
const double x = vals_inp ( 0 );
const double y = vals_inp ( 1 );
const double obj_val = 20 + std::exp ( 1 ) - 20 * std::exp ( - 0.2 * std::sqrt ( 0.5 *(x*x + y*y)) ) - std::exp ( 0.5 *( std::cos ( 2 * OPTIM_PI * x) + std::cos ( 2 * OPTIM_PI * y)) );
return obj_val;
}
int main ()
{
arma::vec x = arma::ones ( 2 , 1 ) + 1.0 ; // initial values: (2,2)
bool success = optim::de (x, ackley_fn, nullptr );
if (success) {
std::cout << " de: Ackley test completed successfully. " << std::endl;
} else {
std::cout << " de: Ackley test completed unsuccessfully. " << std::endl;
}
arma::cout << " de: solution to Ackley test: n " << x << arma::endl;
return 0 ;
}编译并运行:
g++ -Wall -std=c++11 -O3 -march=native -ffp-contract=fast -I/path/to/armadillo -I/path/to/optim/include optim_de_ex.cpp -o optim_de_ex.out -L/path/to/optim/lib -loptim
./optim_de_ex.out检查/tests目录以获取其他示例,以及https://optimlib.readthedocs.io/en/latest/以获取每个算法的详细说明。
对于基于数据的示例,请考虑对logit模型的最大似然估计,该模型在统计和机器学习中常见。在这种情况下,我们对梯度和黑森州具有闭合形式的表达方式。我们将采用流行的梯度下降方法Adam(自适应力矩估计),并与纯牛顿的算法进行比较。
# define OPTIM_ENABLE_ARMA_WRAPPERS
# include " optim.hpp "
// sigmoid function
inline
arma::mat sigm ( const arma::mat& X)
{
return 1.0 / ( 1.0 + arma::exp (-X));
}
// log-likelihood function data
struct ll_data_t
{
arma::vec Y;
arma::mat X;
};
// log-likelihood function with hessian
double ll_fn_whess ( const arma::vec& vals_inp, arma::vec* grad_out, arma::mat* hess_out, void * opt_data)
{
ll_data_t * objfn_data = reinterpret_cast < ll_data_t *>(opt_data);
arma::vec Y = objfn_data-> Y ;
arma::mat X = objfn_data-> X ;
arma::vec mu = sigm (X*vals_inp);
const double norm_term = static_cast < double >(Y. n_elem );
const double obj_val = - arma::accu ( Y% arma::log (mu) + ( 1.0 -Y)% arma::log ( 1.0 -mu) ) / norm_term;
//
if (grad_out)
{
*grad_out = X. t () * (mu - Y) / norm_term;
}
//
if (hess_out)
{
arma::mat S = arma::diagmat ( mu%( 1.0 -mu) );
*hess_out = X. t () * S * X / norm_term;
}
//
return obj_val;
}
// log-likelihood function for Adam
double ll_fn ( const arma::vec& vals_inp, arma::vec* grad_out, void * opt_data)
{
return ll_fn_whess (vals_inp,grad_out, nullptr ,opt_data);
}
//
int main ()
{
int n_dim = 5 ; // dimension of parameter vector
int n_samp = 4000 ; // sample length
arma::mat X = arma::randn (n_samp,n_dim);
arma::vec theta_0 = 1.0 + 3.0 * arma::randu (n_dim, 1 );
arma::vec mu = sigm (X*theta_0);
arma::vec Y (n_samp);
for ( int i= 0 ; i < n_samp; i++)
{
Y (i) = ( arma::as_scalar ( arma::randu ( 1 )) < mu (i) ) ? 1.0 : 0.0 ;
}
// fn data and initial values
ll_data_t opt_data;
opt_data. Y = std::move (Y);
opt_data. X = std::move (X);
arma::vec x = arma::ones (n_dim, 1 ) + 1.0 ; // initial values
// run Adam-based optim
optim:: algo_settings_t settings;
settings. gd_method = 6 ;
settings. gd_settings . step_size = 0.1 ;
std::chrono::time_point<std::chrono::system_clock> start = std::chrono::system_clock::now ();
bool success = optim::gd (x,ll_fn,&opt_data,settings);
std::chrono::time_point<std::chrono::system_clock> end = std::chrono::system_clock::now ();
std::chrono::duration< double > elapsed_seconds = end-start;
//
if (success) {
std::cout << " Adam: logit_reg test completed successfully. n "
<< " elapsed time: " << elapsed_seconds. count () << " s n " ;
} else {
std::cout << " Adam: logit_reg test completed unsuccessfully. " << std::endl;
}
arma::cout << " n Adam: true values vs estimates: n " << arma::join_rows (theta_0,x) << arma::endl;
//
// run Newton-based optim
x = arma::ones (n_dim, 1 ) + 1.0 ; // initial values
start = std::chrono::system_clock::now ();
success = optim::newton (x,ll_fn_whess,&opt_data);
end = std::chrono::system_clock::now ();
elapsed_seconds = end-start;
//
if (success) {
std::cout << " newton: logit_reg test completed successfully. n "
<< " elapsed time: " << elapsed_seconds. count () << " s n " ;
} else {
std::cout << " newton: logit_reg test completed unsuccessfully. " << std::endl;
}
arma::cout << " n newton: true values vs estimates: n " << arma::join_rows (theta_0,x) << arma::endl;
return 0 ;
}输出:
Adam: logit_reg test completed successfully.
elapsed time: 0.025128s
Adam: true values vs estimates:
2.7850 2.6993
3.6561 3.6798
2.3379 2.3860
2.3167 2.4313
2.2465 2.3064
newton: logit_reg test completed successfully.
elapsed time: 0.255909s
newton: true values vs estimates:
2.7850 2.6993
3.6561 3.6798
2.3379 2.3860
2.3167 2.4313
2.2465 2.3064
通过将特定元素与自动库库相结合,Optimlib为自动分化提供了实验支持。
示例使用前向模式自动分化与BFG用于球体功能:
# define OPTIM_ENABLE_EIGEN_WRAPPERS
# include " optim.hpp "
# include < autodiff/forward/real.hpp >
# include < autodiff/forward/real/eigen.hpp >
//
autodiff::real
opt_fnd ( const autodiff::ArrayXreal& x)
{
return x. cwiseProduct (x). sum ();
}
double
opt_fn ( const Eigen::VectorXd& x, Eigen::VectorXd* grad_out, void * opt_data)
{
autodiff::real u;
autodiff::ArrayXreal xd = x. eval ();
if (grad_out) {
Eigen::VectorXd grad_tmp = autodiff::gradient (opt_fnd, autodiff::wrt (xd), autodiff::at (xd), u);
*grad_out = grad_tmp;
} else {
u = opt_fnd (xd);
}
return u. val ();
}
int main ()
{
Eigen::VectorXd x ( 5 );
x << 1 , 2 , 3 , 4 , 5 ;
bool success = optim::bfgs (x, opt_fn, nullptr );
if (success) {
std::cout << " bfgs: forward-mode autodiff test completed successfully. n " << std::endl;
} else {
std::cout << " bfgs: forward-mode autodiff test completed unsuccessfully. n " << std::endl;
}
std::cout << " solution: x = n " << x << std::endl;
return 0 ;
}编译:
g++ -Wall -std=c++17 -O3 -march=native -ffp-contract=fast -I/path/to/eigen -I/path/to/autodiff -I/path/to/optim/include optim_autodiff_ex.cpp -o optim_autodiff_ex.out -L/path/to/optim/lib -loptim有关此主题的更多详细信息,请参见文档。
基思·奥哈拉
Apache版本2