Optimlib는 비선형 함수를위한 수치 최적화 방법의 경량 C ++ 라이브러리입니다.
특징:
float ) 또는 이중 정밀 ( double ) 라이브러리로 제공됩니다.현재 사용 가능한 알고리즘 목록에는 다음이 포함됩니다.
전체 문서는 온라인으로 제공됩니다.
문서의 PDF 버전은 여기에서 제공됩니다.
Optimlib API는 비교적 간단한 규칙을 따릅니다. 대부분의 알고리즘은 다음과 같은 방식으로 호출됩니다.
algorithm_id(<initial/final values>, <objective function>, <objective function data>);
입력은 순서대로 다음과 같습니다.
예를 들어, BFGS 알고리즘을 사용하는 것으로 호출됩니다
bfgs (ColVec_t& init_out_vals, std::function< double ( const ColVec_t& vals_inp, ColVec_t* grad_out, void * opt_data)> opt_objfn, void* opt_data); ColVec_t 사용되는 경우, 예를 들어, arma::vec 또는 Eigen::VectorXd 유형.
Optimlib는 Unix-allike Systems (예 : 인기있는 Linux 기반 배포판 및 MACOS)를위한 컴파일 된 공유 라이브러리 또는 헤더 전용 라이브러리로 제공됩니다. MSVC의 유무에 관계없이 Windows 기반 시스템과 함께이 라이브러리를 사용하는 것은 지원되지 않습니다 .
Optimlib에는 Armadillo 또는 Eigen C ++ 선형 대수 라이브러리가 필요합니다. (Eigen 버전 3.4.0은 C ++ 14 호환 컴파일러가 필요합니다.)
헤더 파일을 포함하기 전에 다음 중 하나를 정의하십시오.
# define OPTIM_ENABLE_ARMA_WRAPPERS
# define OPTIM_ENABLE_EIGEN_WRAPPERS예:
# define OPTIM_ENABLE_EIGEN_WRAPPERS
# include " optim.hpp " 라이브러리는 표준 ./configure && make 방법을 통해 Unix-Alike 시스템에 설치할 수 있습니다.
먼저 라이브러리와 필요한 하위 모듈을 복제하십시오.
# clone optim into the current directory
git clone https://github.com/kthohr/optim ./optim
# change directory
cd ./optim
# clone necessary submodules
git submodule update --init configure 실행하기 전에 다음 환경 변수 중 하나를 설정하십시오.
export ARMA_INCLUDE_PATH=/path/to/armadillo
export EIGEN_INCLUDE_PATH=/path/to/eigen마지막으로:
# build and install with Eigen
./configure -i " /usr/local " -l eigen -p
make
make install 최종 명령은 Optimlib를 /usr/local 에 설치합니다.
구성 옵션 ( ./configure -h 참조) :
주요한
-h 인쇄 도움말-i 설치 경로; 기본값 : 빌드 디렉토리-f 부동 소수점 정밀 모드; 기본값 : double-l 선형 대수 라이브러리 선택을 지정합니다. arma 또는 eigen 선택하십시오-m 링크 할 BLA 및 LAPACK 라이브러리를 지정합니다. 예를 들어 -m "-lopenblas" 또는 -m "-framework Accelerate"-o 컴파일러 최적화 옵션; 기본값으로 -O3 -march=native -ffp-contract=fast -flto -DARMA_NO_DEBUG-p OpenMP 병렬화 기능 활성화 ( 권장 )반성
-c 커버리지 빌드 (Codecov와 함께 사용)-d '개발'빌드-g 디버깅 빌드 (최적화 플래그 -O0 -g 로 설정)특별한
--header-only-version Optimlib의 헤더 전용 버전을 생성합니다 (아래 참조) Optimlib는 헤더 전용 라이브러리로도 제공됩니다 (즉, 공유 라이브러리를 컴파일 할 필요없이). --header-only-version 옵션으로 configure 만하면됩니다.
./configure --header-only-version 이렇게하면 새로운 디렉토리 인 header_only_version 이 생성됩니다. 이 헤더 전용 버전을 사용하면 헤더 파일 ( #include "optim.hpp )을 포함시키고 head_only_version 디렉토리 (예 : -I/path/to/optimlib/header_only_version )에 대한 포함 경로를 설정하십시오.
R 패키지와 함께 Optimlib를 사용하려면 먼저 라이브러리의 헤더 전용 버전을 생성하십시오 (위 참조). 그런 다음 Optimlib 파일을 포함하기 전에 컴파일러 정의를 추가하십시오.
# define OPTIM_USE_RCPP_ARMADILLO
# include " optim.hpp "# define OPTIM_USE_RCPP_EIGEN
# include " optim.hpp " 직장에서 Optimlib를 설명하려면 Ackley 기능의 글로벌 최소 최소 검색을 고려하십시오.
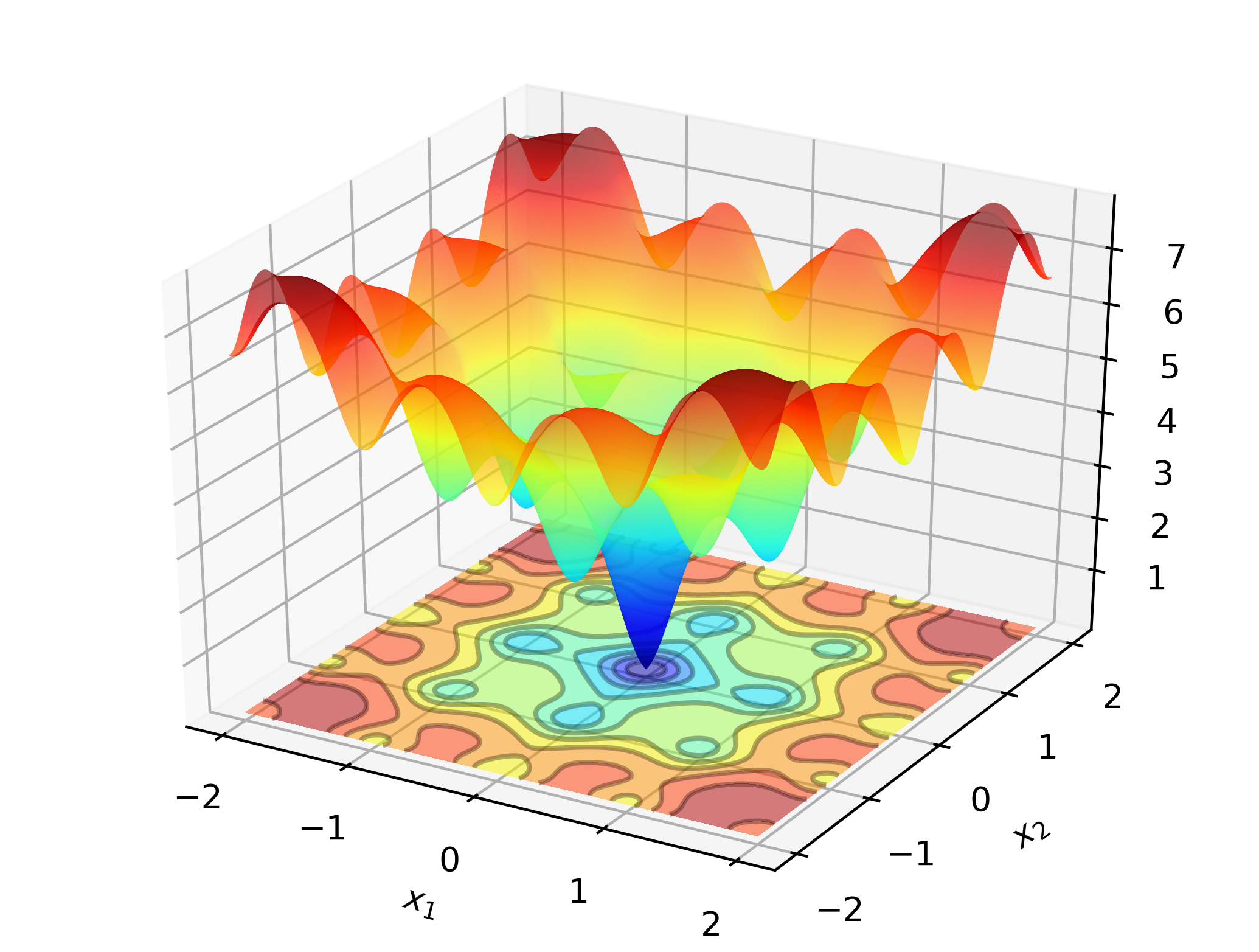
이것은 많은 로컬 미니 마의 잘 알려진 테스트 기능입니다. Newton-Type 방법 (예 : BFG)은 초기 값의 선택에 민감하며 여기서는 다소 제대로 작동하지 않습니다. 따라서 우리는이 경우 차동 진화에 대한 글로벌 검색 방법을 사용할 것입니다.
암호:
# define OPTIM_ENABLE_EIGEN_WRAPPERS
# include " optim.hpp "
# define OPTIM_PI 3.14159265358979
double
ackley_fn ( const Eigen::VectorXd& vals_inp, Eigen::VectorXd* grad_out, void * opt_data)
{
const double x = vals_inp ( 0 );
const double y = vals_inp ( 1 );
const double obj_val = 20 + std::exp ( 1 ) - 20 * std::exp ( - 0.2 * std::sqrt ( 0.5 *(x*x + y*y)) ) - std::exp ( 0.5 *( std::cos ( 2 * OPTIM_PI * x) + std::cos ( 2 * OPTIM_PI * y)) );
return obj_val;
}
int main ()
{
Eigen::VectorXd x = 2.0 * Eigen::VectorXd::Ones ( 2 ); // initial values: (2,2)
bool success = optim::de (x, ackley_fn, nullptr );
if (success) {
std::cout << " de: Ackley test completed successfully. " << std::endl;
} else {
std::cout << " de: Ackley test completed unsuccessfully. " << std::endl;
}
std::cout << " de: solution to Ackley test: n " << x << std::endl;
return 0 ;
}X86 기반 컴퓨터 에서이 예제는 다음을 사용하여 컴파일 할 수 있습니다.
g++ -Wall -std=c++14 -O3 -march=native -ffp-contract=fast -I/path/to/eigen -I/path/to/optim/include optim_de_ex.cpp -o optim_de_ex.out -L/path/to/optim/lib -loptim산출:
de: Ackley test completed successfully.
elapsed time: 0.028167s
de: solution to Ackley test:
-1.2702e-17
-3.8432e-16
표준 노트북에서 Optimlib은 1 초 만에 기계 정밀도에 대한 솔루션을 계산합니다.
이 예제의 Armadillo 기반 버전 :
# define OPTIM_ENABLE_ARMA_WRAPPERS
# include " optim.hpp "
# define OPTIM_PI 3.14159265358979
double
ackley_fn ( const arma::vec& vals_inp, arma::vec* grad_out, void * opt_data)
{
const double x = vals_inp ( 0 );
const double y = vals_inp ( 1 );
const double obj_val = 20 + std::exp ( 1 ) - 20 * std::exp ( - 0.2 * std::sqrt ( 0.5 *(x*x + y*y)) ) - std::exp ( 0.5 *( std::cos ( 2 * OPTIM_PI * x) + std::cos ( 2 * OPTIM_PI * y)) );
return obj_val;
}
int main ()
{
arma::vec x = arma::ones ( 2 , 1 ) + 1.0 ; // initial values: (2,2)
bool success = optim::de (x, ackley_fn, nullptr );
if (success) {
std::cout << " de: Ackley test completed successfully. " << std::endl;
} else {
std::cout << " de: Ackley test completed unsuccessfully. " << std::endl;
}
arma::cout << " de: solution to Ackley test: n " << x << arma::endl;
return 0 ;
}컴파일 및 실행 :
g++ -Wall -std=c++11 -O3 -march=native -ffp-contract=fast -I/path/to/armadillo -I/path/to/optim/include optim_de_ex.cpp -o optim_de_ex.out -L/path/to/optim/lib -loptim
./optim_de_ex.out 추가 예제 /tests 디렉토리를 확인하고 https://optimlib.readthedocs.io/en/latest/를 확인하십시오. 각 알고리즘에 대한 자세한 설명.
데이터 기반 예제의 경우 통계 및 기계 학습에서 공통적 인 로이트 모델의 최대 가능성 추정을 고려하십시오. 이 경우 우리는 그라디언트와 Hessian에 대한 폐쇄 형식 표현이 있습니다. 우리는 인기있는 그라디언트 하강 방법 인 Adam (적응 모멘트 추정)을 사용하고 순수한 Newton 기반 알고리즘과 비교할 것입니다.
# define OPTIM_ENABLE_ARMA_WRAPPERS
# include " optim.hpp "
// sigmoid function
inline
arma::mat sigm ( const arma::mat& X)
{
return 1.0 / ( 1.0 + arma::exp (-X));
}
// log-likelihood function data
struct ll_data_t
{
arma::vec Y;
arma::mat X;
};
// log-likelihood function with hessian
double ll_fn_whess ( const arma::vec& vals_inp, arma::vec* grad_out, arma::mat* hess_out, void * opt_data)
{
ll_data_t * objfn_data = reinterpret_cast < ll_data_t *>(opt_data);
arma::vec Y = objfn_data-> Y ;
arma::mat X = objfn_data-> X ;
arma::vec mu = sigm (X*vals_inp);
const double norm_term = static_cast < double >(Y. n_elem );
const double obj_val = - arma::accu ( Y% arma::log (mu) + ( 1.0 -Y)% arma::log ( 1.0 -mu) ) / norm_term;
//
if (grad_out)
{
*grad_out = X. t () * (mu - Y) / norm_term;
}
//
if (hess_out)
{
arma::mat S = arma::diagmat ( mu%( 1.0 -mu) );
*hess_out = X. t () * S * X / norm_term;
}
//
return obj_val;
}
// log-likelihood function for Adam
double ll_fn ( const arma::vec& vals_inp, arma::vec* grad_out, void * opt_data)
{
return ll_fn_whess (vals_inp,grad_out, nullptr ,opt_data);
}
//
int main ()
{
int n_dim = 5 ; // dimension of parameter vector
int n_samp = 4000 ; // sample length
arma::mat X = arma::randn (n_samp,n_dim);
arma::vec theta_0 = 1.0 + 3.0 * arma::randu (n_dim, 1 );
arma::vec mu = sigm (X*theta_0);
arma::vec Y (n_samp);
for ( int i= 0 ; i < n_samp; i++)
{
Y (i) = ( arma::as_scalar ( arma::randu ( 1 )) < mu (i) ) ? 1.0 : 0.0 ;
}
// fn data and initial values
ll_data_t opt_data;
opt_data. Y = std::move (Y);
opt_data. X = std::move (X);
arma::vec x = arma::ones (n_dim, 1 ) + 1.0 ; // initial values
// run Adam-based optim
optim:: algo_settings_t settings;
settings. gd_method = 6 ;
settings. gd_settings . step_size = 0.1 ;
std::chrono::time_point<std::chrono::system_clock> start = std::chrono::system_clock::now ();
bool success = optim::gd (x,ll_fn,&opt_data,settings);
std::chrono::time_point<std::chrono::system_clock> end = std::chrono::system_clock::now ();
std::chrono::duration< double > elapsed_seconds = end-start;
//
if (success) {
std::cout << " Adam: logit_reg test completed successfully. n "
<< " elapsed time: " << elapsed_seconds. count () << " s n " ;
} else {
std::cout << " Adam: logit_reg test completed unsuccessfully. " << std::endl;
}
arma::cout << " n Adam: true values vs estimates: n " << arma::join_rows (theta_0,x) << arma::endl;
//
// run Newton-based optim
x = arma::ones (n_dim, 1 ) + 1.0 ; // initial values
start = std::chrono::system_clock::now ();
success = optim::newton (x,ll_fn_whess,&opt_data);
end = std::chrono::system_clock::now ();
elapsed_seconds = end-start;
//
if (success) {
std::cout << " newton: logit_reg test completed successfully. n "
<< " elapsed time: " << elapsed_seconds. count () << " s n " ;
} else {
std::cout << " newton: logit_reg test completed unsuccessfully. " << std::endl;
}
arma::cout << " n newton: true values vs estimates: n " << arma::join_rows (theta_0,x) << arma::endl;
return 0 ;
}산출:
Adam: logit_reg test completed successfully.
elapsed time: 0.025128s
Adam: true values vs estimates:
2.7850 2.6993
3.6561 3.6798
2.3379 2.3860
2.3167 2.4313
2.2465 2.3064
newton: logit_reg test completed successfully.
elapsed time: 0.255909s
newton: true values vs estimates:
2.7850 2.6993
3.6561 3.6798
2.3379 2.3860
2.3167 2.4313
2.2465 2.3064
Eigen을 Autodiff 라이브러리와 결합하여 Optimlib는 자동 차별화에 대한 실험적 지원을 제공합니다.
구체 함수를 위해 BFG와 함께 전방 모드 자동 차별화를 사용하는 예 :
# define OPTIM_ENABLE_EIGEN_WRAPPERS
# include " optim.hpp "
# include < autodiff/forward/real.hpp >
# include < autodiff/forward/real/eigen.hpp >
//
autodiff::real
opt_fnd ( const autodiff::ArrayXreal& x)
{
return x. cwiseProduct (x). sum ();
}
double
opt_fn ( const Eigen::VectorXd& x, Eigen::VectorXd* grad_out, void * opt_data)
{
autodiff::real u;
autodiff::ArrayXreal xd = x. eval ();
if (grad_out) {
Eigen::VectorXd grad_tmp = autodiff::gradient (opt_fnd, autodiff::wrt (xd), autodiff::at (xd), u);
*grad_out = grad_tmp;
} else {
u = opt_fnd (xd);
}
return u. val ();
}
int main ()
{
Eigen::VectorXd x ( 5 );
x << 1 , 2 , 3 , 4 , 5 ;
bool success = optim::bfgs (x, opt_fn, nullptr );
if (success) {
std::cout << " bfgs: forward-mode autodiff test completed successfully. n " << std::endl;
} else {
std::cout << " bfgs: forward-mode autodiff test completed unsuccessfully. n " << std::endl;
}
std::cout << " solution: x = n " << x << std::endl;
return 0 ;
}컴파일 :
g++ -Wall -std=c++17 -O3 -march=native -ffp-contract=fast -I/path/to/eigen -I/path/to/autodiff -I/path/to/optim/include optim_autodiff_ex.cpp -o optim_autodiff_ex.out -L/path/to/optim/lib -loptim이 주제에 대한 자세한 내용은 문서를 참조하십시오.
키이스 오하라
아파치 버전 2