O Optimlib é uma biblioteca C ++ leve de métodos de otimização numérica para funções não lineares.
Características:
float ) ou dupla precisão ( double ).Uma lista de algoritmos atualmente disponíveis inclui:
A documentação completa está disponível online:
Uma versão em PDF da documentação está disponível aqui.
A API Optimlib segue uma convenção relativamente simples, com a maioria dos algoritmos chamados da seguinte maneira:
algorithm_id(<initial/final values>, <objective function>, <objective function data>);
As entradas, em ordem, são:
Por exemplo, o algoritmo BFGS é chamado usando
bfgs (ColVec_t& init_out_vals, std::function< double ( const ColVec_t& vals_inp, ColVec_t* grad_out, void * opt_data)> opt_objfn, void* opt_data); Onde ColVec_t é usado para representar, por exemplo, arma::vec ou Eigen::VectorXd Tipos.
O Optimlib está disponível como uma biblioteca compartilhada compilada, ou como biblioteca somente para cabeçalho, apenas para sistemas unix-beike (por exemplo, distritos populares baseados em Linux, bem como macOS). O uso desta biblioteca com sistemas baseados no Windows, com ou sem MSVC, não é suportado .
O Optimlib requer as bibliotecas de álgebra linear de Armadillo ou Eigen C ++. (Observe que a versão Eigen 3.4.0 requer um compilador compatível com C ++ 14 compatível.)
Antes de incluir os arquivos do cabeçalho, defina um dos seguintes:
# define OPTIM_ENABLE_ARMA_WRAPPERS
# define OPTIM_ENABLE_EIGEN_WRAPPERSExemplo:
# define OPTIM_ENABLE_EIGEN_WRAPPERS
# include " optim.hpp " A biblioteca pode ser instalada em sistemas UNIX-ALIQUELA através do método padrão ./configure && make .
Primeiro clone a biblioteca e quaisquer submódulos necessários:
# clone optim into the current directory
git clone https://github.com/kthohr/optim ./optim
# change directory
cd ./optim
# clone necessary submodules
git submodule update --init Conjunto (um) das seguintes variáveis de ambiente antes de executar configure :
export ARMA_INCLUDE_PATH=/path/to/armadillo
export EIGEN_INCLUDE_PATH=/path/to/eigenFinalmente:
# build and install with Eigen
./configure -i " /usr/local " -l eigen -p
make
make install O comando final instalará o Optimlib em /usr/local .
Opções de configuração (consulte ./configure -h ):
Primário
-h Imprima ajuda-i Caminho de instalação; Padrão: o diretório de construção-f modo de precisão de ponto flutuante; Padrão: double-l Especifique a escolha da biblioteca de álgebra linear; Escolha arma ou eigen-m Especifique as bibliotecas BLAs e lambe as links para vincular; Por exemplo, -m "-lopenblas" ou -m "-framework Accelerate"-o Opções de otimização do compilador; Padrão para -O3 -march=native -ffp-contract=fast -flto -DARMA_NO_DEBUG-p Ativar recursos de paralelização do OpenMP ( recomendado )Secundário
-c uma construção de cobertura (usada com codecov)-d uma construção de 'desenvolvimento'-g uma construção de depuração (sinalizadores de otimização definidos como -O0 -g )Especial
--header-only-version Gere uma versão somente para cabeçalho do Optimlib (veja abaixo) O Optimlib também está disponível como uma biblioteca somente para cabeçalho (ou seja, sem a necessidade de compilar uma biblioteca compartilhada). Basta executar configure com a opção --header-only-version :
./configure --header-only-version Isso criará um novo diretório, header_only_version , contendo uma cópia do Optimlib, modificada para trabalhar em linha. Com esta versão somente para cabeçalho, basta incluir os arquivos do cabeçalho ( #include "optim.hpp ) e defina o caminho de incluir no diretório head_only_version (por exemplo, -I/path/to/optimlib/header_only_version ).
Para usar o Optimlib com um pacote R, primeiro gere uma versão somente para cabeçalho da biblioteca (veja acima). Em seguida, basta adicionar uma definição de compilador antes de incluir os arquivos OptimLib.
# define OPTIM_USE_RCPP_ARMADILLO
# include " optim.hpp "# define OPTIM_USE_RCPP_EIGEN
# include " optim.hpp " Para ilustrar o Optimlib no trabalho, considere procurar o mínimo global da função Ackley:
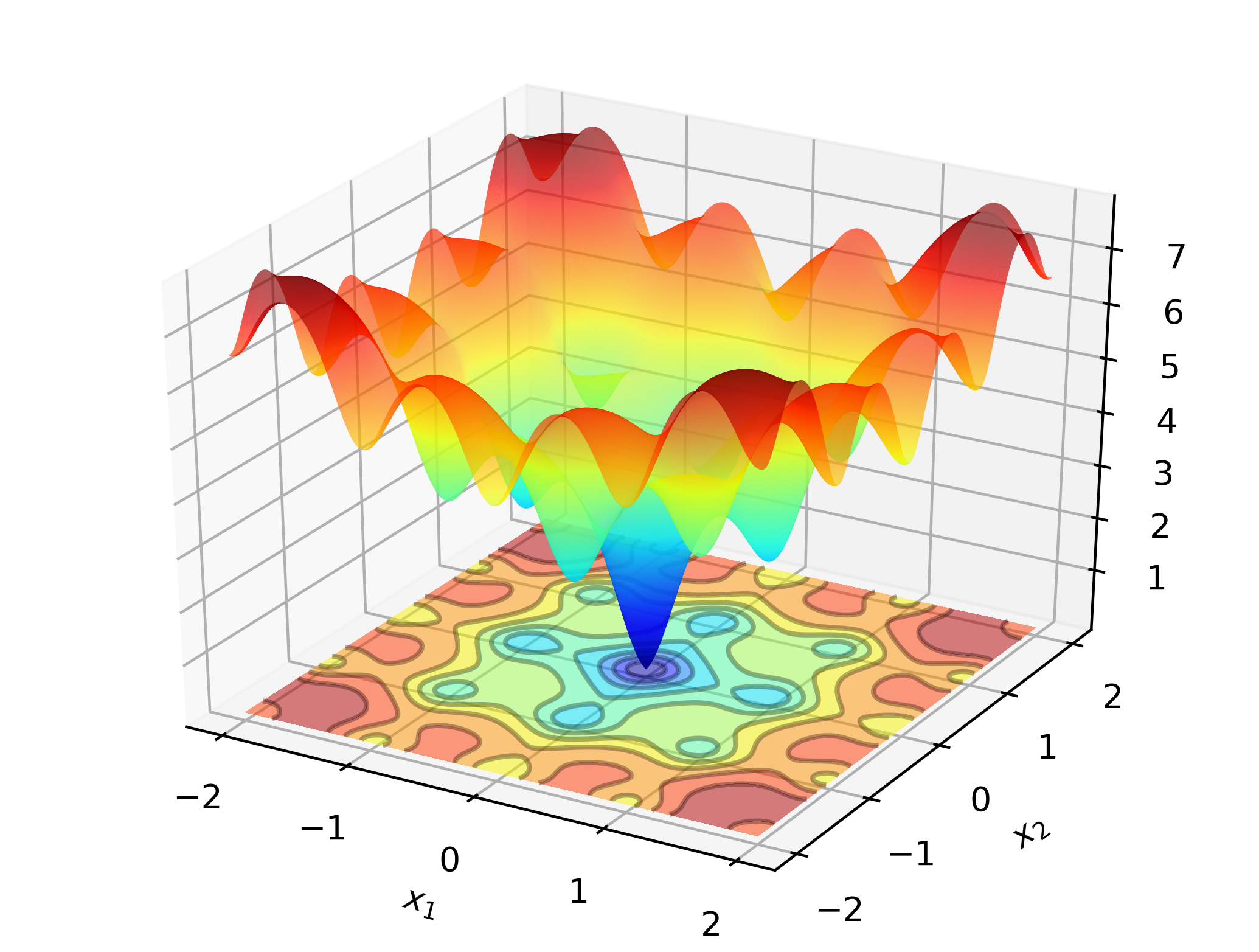
Esta é uma função de teste bem conhecida com muitos mínimos locais. Os métodos do tipo Newton (como o BFGS) são sensíveis à escolha dos valores iniciais e terão um desempenho ruim aqui. Como tal, empregaremos um método de pesquisa global-neste caso: evolução diferencial.
Código:
# define OPTIM_ENABLE_EIGEN_WRAPPERS
# include " optim.hpp "
# define OPTIM_PI 3.14159265358979
double
ackley_fn ( const Eigen::VectorXd& vals_inp, Eigen::VectorXd* grad_out, void * opt_data)
{
const double x = vals_inp ( 0 );
const double y = vals_inp ( 1 );
const double obj_val = 20 + std::exp ( 1 ) - 20 * std::exp ( - 0.2 * std::sqrt ( 0.5 *(x*x + y*y)) ) - std::exp ( 0.5 *( std::cos ( 2 * OPTIM_PI * x) + std::cos ( 2 * OPTIM_PI * y)) );
return obj_val;
}
int main ()
{
Eigen::VectorXd x = 2.0 * Eigen::VectorXd::Ones ( 2 ); // initial values: (2,2)
bool success = optim::de (x, ackley_fn, nullptr );
if (success) {
std::cout << " de: Ackley test completed successfully. " << std::endl;
} else {
std::cout << " de: Ackley test completed unsuccessfully. " << std::endl;
}
std::cout << " de: solution to Ackley test: n " << x << std::endl;
return 0 ;
}Nos computadores baseados em x86, este exemplo pode ser compilado usando:
g++ -Wall -std=c++14 -O3 -march=native -ffp-contract=fast -I/path/to/eigen -I/path/to/optim/include optim_de_ex.cpp -o optim_de_ex.out -L/path/to/optim/lib -loptimSaída:
de: Ackley test completed successfully.
elapsed time: 0.028167s
de: solution to Ackley test:
-1.2702e-17
-3.8432e-16
Em um laptop padrão, o Optimlib calculará uma solução para dentro da precisão da máquina em uma fração de segundo.
A versão baseada em Armadillo deste exemplo:
# define OPTIM_ENABLE_ARMA_WRAPPERS
# include " optim.hpp "
# define OPTIM_PI 3.14159265358979
double
ackley_fn ( const arma::vec& vals_inp, arma::vec* grad_out, void * opt_data)
{
const double x = vals_inp ( 0 );
const double y = vals_inp ( 1 );
const double obj_val = 20 + std::exp ( 1 ) - 20 * std::exp ( - 0.2 * std::sqrt ( 0.5 *(x*x + y*y)) ) - std::exp ( 0.5 *( std::cos ( 2 * OPTIM_PI * x) + std::cos ( 2 * OPTIM_PI * y)) );
return obj_val;
}
int main ()
{
arma::vec x = arma::ones ( 2 , 1 ) + 1.0 ; // initial values: (2,2)
bool success = optim::de (x, ackley_fn, nullptr );
if (success) {
std::cout << " de: Ackley test completed successfully. " << std::endl;
} else {
std::cout << " de: Ackley test completed unsuccessfully. " << std::endl;
}
arma::cout << " de: solution to Ackley test: n " << x << arma::endl;
return 0 ;
}Compilar e executar:
g++ -Wall -std=c++11 -O3 -march=native -ffp-contract=fast -I/path/to/armadillo -I/path/to/optim/include optim_de_ex.cpp -o optim_de_ex.out -L/path/to/optim/lib -loptim
./optim_de_ex.out Verifique o diretório /tests para obter exemplos adicionais, e https://optimlib.readthedocs.io/en/latest/ para obter uma descrição detalhada de cada algoritmo.
Para um exemplo baseado em dados, considere a estimativa máxima de probabilidade de um modelo de logit, comum em estatística e aprendizado de máquina. Nesse caso, temos expressões de forma fechada para o gradiente e Hessiano. Empregaremos um método de descida de gradiente popular, Adam (estimativa de momento adaptativo) e compararemos com um algoritmo puro baseado em Newton.
# define OPTIM_ENABLE_ARMA_WRAPPERS
# include " optim.hpp "
// sigmoid function
inline
arma::mat sigm ( const arma::mat& X)
{
return 1.0 / ( 1.0 + arma::exp (-X));
}
// log-likelihood function data
struct ll_data_t
{
arma::vec Y;
arma::mat X;
};
// log-likelihood function with hessian
double ll_fn_whess ( const arma::vec& vals_inp, arma::vec* grad_out, arma::mat* hess_out, void * opt_data)
{
ll_data_t * objfn_data = reinterpret_cast < ll_data_t *>(opt_data);
arma::vec Y = objfn_data-> Y ;
arma::mat X = objfn_data-> X ;
arma::vec mu = sigm (X*vals_inp);
const double norm_term = static_cast < double >(Y. n_elem );
const double obj_val = - arma::accu ( Y% arma::log (mu) + ( 1.0 -Y)% arma::log ( 1.0 -mu) ) / norm_term;
//
if (grad_out)
{
*grad_out = X. t () * (mu - Y) / norm_term;
}
//
if (hess_out)
{
arma::mat S = arma::diagmat ( mu%( 1.0 -mu) );
*hess_out = X. t () * S * X / norm_term;
}
//
return obj_val;
}
// log-likelihood function for Adam
double ll_fn ( const arma::vec& vals_inp, arma::vec* grad_out, void * opt_data)
{
return ll_fn_whess (vals_inp,grad_out, nullptr ,opt_data);
}
//
int main ()
{
int n_dim = 5 ; // dimension of parameter vector
int n_samp = 4000 ; // sample length
arma::mat X = arma::randn (n_samp,n_dim);
arma::vec theta_0 = 1.0 + 3.0 * arma::randu (n_dim, 1 );
arma::vec mu = sigm (X*theta_0);
arma::vec Y (n_samp);
for ( int i= 0 ; i < n_samp; i++)
{
Y (i) = ( arma::as_scalar ( arma::randu ( 1 )) < mu (i) ) ? 1.0 : 0.0 ;
}
// fn data and initial values
ll_data_t opt_data;
opt_data. Y = std::move (Y);
opt_data. X = std::move (X);
arma::vec x = arma::ones (n_dim, 1 ) + 1.0 ; // initial values
// run Adam-based optim
optim:: algo_settings_t settings;
settings. gd_method = 6 ;
settings. gd_settings . step_size = 0.1 ;
std::chrono::time_point<std::chrono::system_clock> start = std::chrono::system_clock::now ();
bool success = optim::gd (x,ll_fn,&opt_data,settings);
std::chrono::time_point<std::chrono::system_clock> end = std::chrono::system_clock::now ();
std::chrono::duration< double > elapsed_seconds = end-start;
//
if (success) {
std::cout << " Adam: logit_reg test completed successfully. n "
<< " elapsed time: " << elapsed_seconds. count () << " s n " ;
} else {
std::cout << " Adam: logit_reg test completed unsuccessfully. " << std::endl;
}
arma::cout << " n Adam: true values vs estimates: n " << arma::join_rows (theta_0,x) << arma::endl;
//
// run Newton-based optim
x = arma::ones (n_dim, 1 ) + 1.0 ; // initial values
start = std::chrono::system_clock::now ();
success = optim::newton (x,ll_fn_whess,&opt_data);
end = std::chrono::system_clock::now ();
elapsed_seconds = end-start;
//
if (success) {
std::cout << " newton: logit_reg test completed successfully. n "
<< " elapsed time: " << elapsed_seconds. count () << " s n " ;
} else {
std::cout << " newton: logit_reg test completed unsuccessfully. " << std::endl;
}
arma::cout << " n newton: true values vs estimates: n " << arma::join_rows (theta_0,x) << arma::endl;
return 0 ;
}Saída:
Adam: logit_reg test completed successfully.
elapsed time: 0.025128s
Adam: true values vs estimates:
2.7850 2.6993
3.6561 3.6798
2.3379 2.3860
2.3167 2.4313
2.2465 2.3064
newton: logit_reg test completed successfully.
elapsed time: 0.255909s
newton: true values vs estimates:
2.7850 2.6993
3.6561 3.6798
2.3379 2.3860
2.3167 2.4313
2.2465 2.3064
Ao combinar Eigen com a Biblioteca Autodiff, o Optimlib fornece suporte experimental para diferenciação automática.
Exemplo usando diferenciação automática no modo avançado com BFGs para a função da esfera:
# define OPTIM_ENABLE_EIGEN_WRAPPERS
# include " optim.hpp "
# include < autodiff/forward/real.hpp >
# include < autodiff/forward/real/eigen.hpp >
//
autodiff::real
opt_fnd ( const autodiff::ArrayXreal& x)
{
return x. cwiseProduct (x). sum ();
}
double
opt_fn ( const Eigen::VectorXd& x, Eigen::VectorXd* grad_out, void * opt_data)
{
autodiff::real u;
autodiff::ArrayXreal xd = x. eval ();
if (grad_out) {
Eigen::VectorXd grad_tmp = autodiff::gradient (opt_fnd, autodiff::wrt (xd), autodiff::at (xd), u);
*grad_out = grad_tmp;
} else {
u = opt_fnd (xd);
}
return u. val ();
}
int main ()
{
Eigen::VectorXd x ( 5 );
x << 1 , 2 , 3 , 4 , 5 ;
bool success = optim::bfgs (x, opt_fn, nullptr );
if (success) {
std::cout << " bfgs: forward-mode autodiff test completed successfully. n " << std::endl;
} else {
std::cout << " bfgs: forward-mode autodiff test completed unsuccessfully. n " << std::endl;
}
std::cout << " solution: x = n " << x << std::endl;
return 0 ;
}Compilar com:
g++ -Wall -std=c++17 -O3 -march=native -ffp-contract=fast -I/path/to/eigen -I/path/to/autodiff -I/path/to/optim/include optim_autodiff_ex.cpp -o optim_autodiff_ex.out -L/path/to/optim/lib -loptimConsulte a documentação para obter mais detalhes sobre este tópico.
Keith O'Hara
Apache versão 2