Optimlib est une bibliothèque C ++ légère de méthodes d'optimisation numérique pour les fonctions non linéaires.
Caractéristiques:
float ) ou de double précision ( double ).Une liste des algorithmes actuellement disponibles comprend:
La documentation complète est disponible en ligne:
Une version PDF de la documentation est disponible ici.
L'API OptimLib suit une convention relativement simple, avec la plupart des algorithmes appelés de la manière suivante:
algorithm_id(<initial/final values>, <objective function>, <objective function data>);
Les entrées, dans l'ordre, sont:
Par exemple, l'algorithme BFGS est appelé
bfgs (ColVec_t& init_out_vals, std::function< double ( const ColVec_t& vals_inp, ColVec_t* grad_out, void * opt_data)> opt_objfn, void* opt_data); où ColVec_t est utilisé pour représenter, par exemple, arma::vec ou Eigen::VectorXd types.
Optimlib est disponible en bibliothèque partagée compilée, ou en bibliothèque d'en-tête uniquement, pour les systèmes Unix-Alike uniquement (par exemple, les distros populaires basés sur Linux, ainsi que MacOS). L'utilisation de cette bibliothèque avec des systèmes Windows, avec ou sans MSVC, n'est pas prise en charge .
Optimlib nécessite les bibliothèques d'algèbre linéaire de l'Armadillo ou de Eigen C ++. (Notez que Eigen version 3.4.0 nécessite un compilateur compatible C ++ 14.)
Avant d'inclure les fichiers d'en-tête, définissez l'une des opérations suivantes:
# define OPTIM_ENABLE_ARMA_WRAPPERS
# define OPTIM_ENABLE_EIGEN_WRAPPERSExemple:
# define OPTIM_ENABLE_EIGEN_WRAPPERS
# include " optim.hpp " La bibliothèque peut être installée sur les systèmes Unix-Alike via la méthode standard ./configure && make .
Clone d'abord la bibliothèque et tout sous-module nécessaire:
# clone optim into the current directory
git clone https://github.com/kthohr/optim ./optim
# change directory
cd ./optim
# clone necessary submodules
git submodule update --init Définir (un) des variables d'environnement suivantes avant d'exécuter configure :
export ARMA_INCLUDE_PATH=/path/to/armadillo
export EIGEN_INCLUDE_PATH=/path/to/eigenEnfin:
# build and install with Eigen
./configure -i " /usr/local " -l eigen -p
make
make install La commande finale installera OptimLib dans /usr/local .
Options de configuration (voir ./configure -h ):
Primaire
-h aide à l'impression-i chemin d'installation; Par défaut: le répertoire de build-f mode de précision à virgule flottante; par défaut: double-l Spécifiez le choix de la bibliothèque d'algèbre linéaire; Choisissez arma ou eigen-m Spécifiez les bibliothèques BLAS et LAPACK avec lesquelles vous liez; Par exemple, -m "-lopenblas" ou -m "-framework Accelerate"-o options d'optimisation du compilateur; par défaut à -O3 -march=native -ffp-contract=fast -flto -DARMA_NO_DEBUG-p Activer les fonctionnalités de parallélisation OpenMP ( recommandée )Secondaire
-c une version de couverture (utilisée avec Codecov)-d une construction de «développement»-g une construction de débogage (indicateurs d'optimisation définis sur -O0 -g )Spécial
--header-only-version Générer une version d'en-tête uniquement d'OptimLib (voir ci-dessous) OptimLib est également disponible en tant que bibliothèque d'en-tête uniquement (c'est-à-dire sans avoir besoin de compiler une bibliothèque partagée). Exécutez simplement configure avec l'option --header-only-version :
./configure --header-only-version Cela créera un nouveau répertoire, header_only_version , contenant une copie d'OptimLib, modifiée pour fonctionner en ligne. Avec cette version d'en-tête uniquement, incluez simplement les fichiers d'en-tête ( #include "optim.hpp ) et définissez le chemin d'inclusion vers le répertoire head_only_version (par exemple, -I/path/to/optimlib/header_only_version ).
Pour utiliser OptimLib avec un package R, générez d'abord une version d'en-tête uniquement de la bibliothèque (voir ci-dessus). Ensuite, ajoutez simplement une définition du compilateur avant d'inclure les fichiers OptimLib.
# define OPTIM_USE_RCPP_ARMADILLO
# include " optim.hpp "# define OPTIM_USE_RCPP_EIGEN
# include " optim.hpp " Pour illustrer Optimlib au travail, envisagez de rechercher le minimum global de la fonction Ackley:
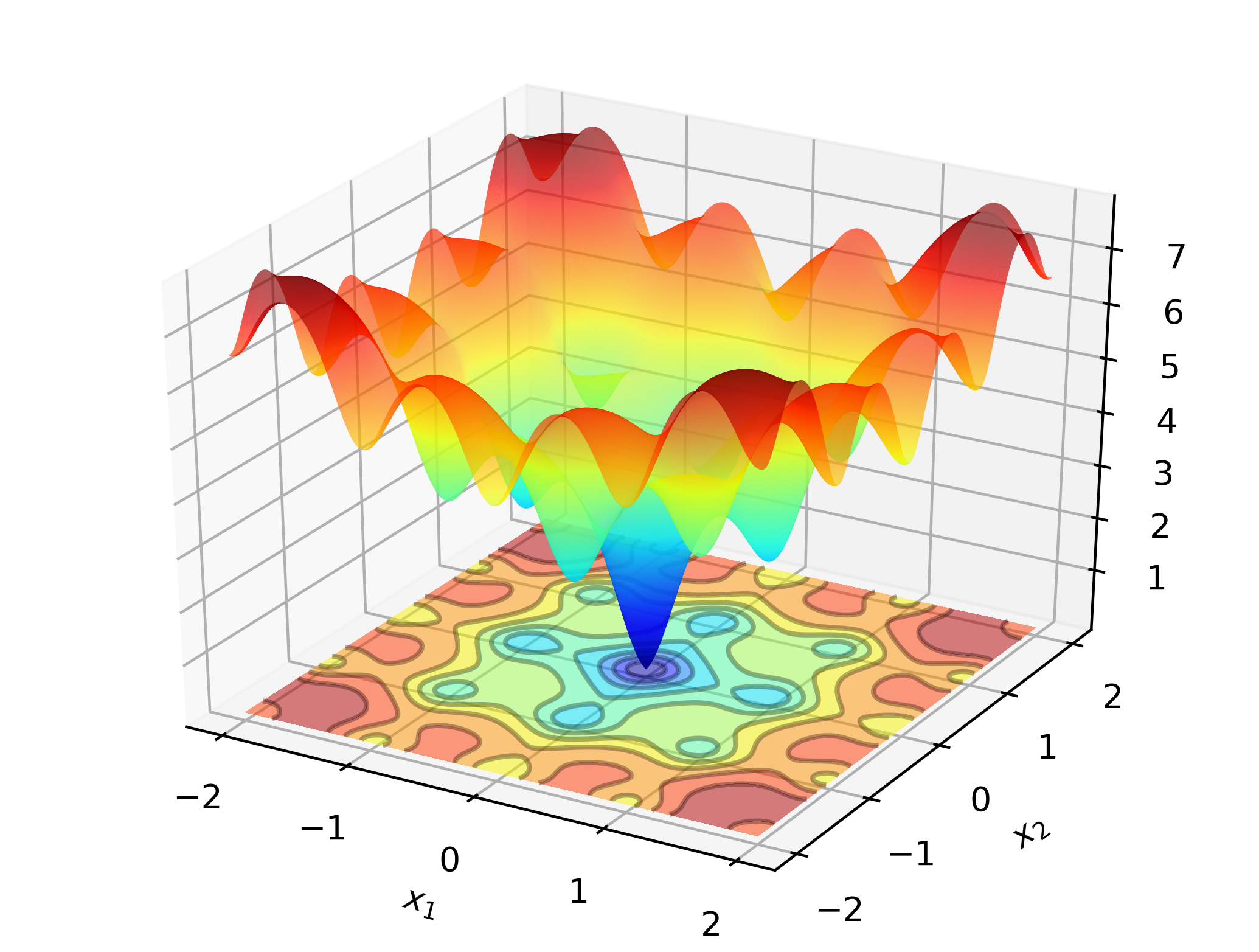
Il s'agit d'une fonction de test bien connue avec de nombreux minima locaux. Les méthodes de type Newton (telles que les BFG) sont sensibles au choix des valeurs initiales et se comporteront plutôt mal ici. En tant que tel, nous utiliserons une méthode de recherche globale - dans ce cas: l'évolution différentielle.
Code:
# define OPTIM_ENABLE_EIGEN_WRAPPERS
# include " optim.hpp "
# define OPTIM_PI 3.14159265358979
double
ackley_fn ( const Eigen::VectorXd& vals_inp, Eigen::VectorXd* grad_out, void * opt_data)
{
const double x = vals_inp ( 0 );
const double y = vals_inp ( 1 );
const double obj_val = 20 + std::exp ( 1 ) - 20 * std::exp ( - 0.2 * std::sqrt ( 0.5 *(x*x + y*y)) ) - std::exp ( 0.5 *( std::cos ( 2 * OPTIM_PI * x) + std::cos ( 2 * OPTIM_PI * y)) );
return obj_val;
}
int main ()
{
Eigen::VectorXd x = 2.0 * Eigen::VectorXd::Ones ( 2 ); // initial values: (2,2)
bool success = optim::de (x, ackley_fn, nullptr );
if (success) {
std::cout << " de: Ackley test completed successfully. " << std::endl;
} else {
std::cout << " de: Ackley test completed unsuccessfully. " << std::endl;
}
std::cout << " de: solution to Ackley test: n " << x << std::endl;
return 0 ;
}Sur les ordinateurs basés sur x86, cet exemple peut être compilé en utilisant:
g++ -Wall -std=c++14 -O3 -march=native -ffp-contract=fast -I/path/to/eigen -I/path/to/optim/include optim_de_ex.cpp -o optim_de_ex.out -L/path/to/optim/lib -loptimSortir:
de: Ackley test completed successfully.
elapsed time: 0.028167s
de: solution to Ackley test:
-1.2702e-17
-3.8432e-16
Sur un ordinateur portable standard, OptimLib calculera une solution à la précision de la machine dans une fraction de seconde.
La version basée sur le tas de cet exemple:
# define OPTIM_ENABLE_ARMA_WRAPPERS
# include " optim.hpp "
# define OPTIM_PI 3.14159265358979
double
ackley_fn ( const arma::vec& vals_inp, arma::vec* grad_out, void * opt_data)
{
const double x = vals_inp ( 0 );
const double y = vals_inp ( 1 );
const double obj_val = 20 + std::exp ( 1 ) - 20 * std::exp ( - 0.2 * std::sqrt ( 0.5 *(x*x + y*y)) ) - std::exp ( 0.5 *( std::cos ( 2 * OPTIM_PI * x) + std::cos ( 2 * OPTIM_PI * y)) );
return obj_val;
}
int main ()
{
arma::vec x = arma::ones ( 2 , 1 ) + 1.0 ; // initial values: (2,2)
bool success = optim::de (x, ackley_fn, nullptr );
if (success) {
std::cout << " de: Ackley test completed successfully. " << std::endl;
} else {
std::cout << " de: Ackley test completed unsuccessfully. " << std::endl;
}
arma::cout << " de: solution to Ackley test: n " << x << arma::endl;
return 0 ;
}Compiler et courir:
g++ -Wall -std=c++11 -O3 -march=native -ffp-contract=fast -I/path/to/armadillo -I/path/to/optim/include optim_de_ex.cpp -o optim_de_ex.out -L/path/to/optim/lib -loptim
./optim_de_ex.out Vérifiez le répertoire /tests pour des exemples supplémentaires et https://optimlib.readthedocs.io/en/latest/ pour une description détaillée de chaque algorithme.
Pour un exemple basé sur les données, considérons l'estimation du maximum de vraisemblance d'un modèle logit, commun dans les statistiques et l'apprentissage automatique. Dans ce cas, nous avons des expressions de forme fermée pour le gradient et la Hesse. Nous utiliserons une méthode de descente de gradient populaire, Adam (estimation du moment adaptatif) et se comparerons à un algorithme pur à Newton.
# define OPTIM_ENABLE_ARMA_WRAPPERS
# include " optim.hpp "
// sigmoid function
inline
arma::mat sigm ( const arma::mat& X)
{
return 1.0 / ( 1.0 + arma::exp (-X));
}
// log-likelihood function data
struct ll_data_t
{
arma::vec Y;
arma::mat X;
};
// log-likelihood function with hessian
double ll_fn_whess ( const arma::vec& vals_inp, arma::vec* grad_out, arma::mat* hess_out, void * opt_data)
{
ll_data_t * objfn_data = reinterpret_cast < ll_data_t *>(opt_data);
arma::vec Y = objfn_data-> Y ;
arma::mat X = objfn_data-> X ;
arma::vec mu = sigm (X*vals_inp);
const double norm_term = static_cast < double >(Y. n_elem );
const double obj_val = - arma::accu ( Y% arma::log (mu) + ( 1.0 -Y)% arma::log ( 1.0 -mu) ) / norm_term;
//
if (grad_out)
{
*grad_out = X. t () * (mu - Y) / norm_term;
}
//
if (hess_out)
{
arma::mat S = arma::diagmat ( mu%( 1.0 -mu) );
*hess_out = X. t () * S * X / norm_term;
}
//
return obj_val;
}
// log-likelihood function for Adam
double ll_fn ( const arma::vec& vals_inp, arma::vec* grad_out, void * opt_data)
{
return ll_fn_whess (vals_inp,grad_out, nullptr ,opt_data);
}
//
int main ()
{
int n_dim = 5 ; // dimension of parameter vector
int n_samp = 4000 ; // sample length
arma::mat X = arma::randn (n_samp,n_dim);
arma::vec theta_0 = 1.0 + 3.0 * arma::randu (n_dim, 1 );
arma::vec mu = sigm (X*theta_0);
arma::vec Y (n_samp);
for ( int i= 0 ; i < n_samp; i++)
{
Y (i) = ( arma::as_scalar ( arma::randu ( 1 )) < mu (i) ) ? 1.0 : 0.0 ;
}
// fn data and initial values
ll_data_t opt_data;
opt_data. Y = std::move (Y);
opt_data. X = std::move (X);
arma::vec x = arma::ones (n_dim, 1 ) + 1.0 ; // initial values
// run Adam-based optim
optim:: algo_settings_t settings;
settings. gd_method = 6 ;
settings. gd_settings . step_size = 0.1 ;
std::chrono::time_point<std::chrono::system_clock> start = std::chrono::system_clock::now ();
bool success = optim::gd (x,ll_fn,&opt_data,settings);
std::chrono::time_point<std::chrono::system_clock> end = std::chrono::system_clock::now ();
std::chrono::duration< double > elapsed_seconds = end-start;
//
if (success) {
std::cout << " Adam: logit_reg test completed successfully. n "
<< " elapsed time: " << elapsed_seconds. count () << " s n " ;
} else {
std::cout << " Adam: logit_reg test completed unsuccessfully. " << std::endl;
}
arma::cout << " n Adam: true values vs estimates: n " << arma::join_rows (theta_0,x) << arma::endl;
//
// run Newton-based optim
x = arma::ones (n_dim, 1 ) + 1.0 ; // initial values
start = std::chrono::system_clock::now ();
success = optim::newton (x,ll_fn_whess,&opt_data);
end = std::chrono::system_clock::now ();
elapsed_seconds = end-start;
//
if (success) {
std::cout << " newton: logit_reg test completed successfully. n "
<< " elapsed time: " << elapsed_seconds. count () << " s n " ;
} else {
std::cout << " newton: logit_reg test completed unsuccessfully. " << std::endl;
}
arma::cout << " n newton: true values vs estimates: n " << arma::join_rows (theta_0,x) << arma::endl;
return 0 ;
}Sortir:
Adam: logit_reg test completed successfully.
elapsed time: 0.025128s
Adam: true values vs estimates:
2.7850 2.6993
3.6561 3.6798
2.3379 2.3860
2.3167 2.4313
2.2465 2.3064
newton: logit_reg test completed successfully.
elapsed time: 0.255909s
newton: true values vs estimates:
2.7850 2.6993
3.6561 3.6798
2.3379 2.3860
2.3167 2.4313
2.2465 2.3064
En combinant Eigen avec la bibliothèque Autodiff, Optimlib fournit un support expérimental pour la différenciation automatique.
Exemple utilisant la différenciation automatique en mode avant avec BFGS pour la fonction SPHERE:
# define OPTIM_ENABLE_EIGEN_WRAPPERS
# include " optim.hpp "
# include < autodiff/forward/real.hpp >
# include < autodiff/forward/real/eigen.hpp >
//
autodiff::real
opt_fnd ( const autodiff::ArrayXreal& x)
{
return x. cwiseProduct (x). sum ();
}
double
opt_fn ( const Eigen::VectorXd& x, Eigen::VectorXd* grad_out, void * opt_data)
{
autodiff::real u;
autodiff::ArrayXreal xd = x. eval ();
if (grad_out) {
Eigen::VectorXd grad_tmp = autodiff::gradient (opt_fnd, autodiff::wrt (xd), autodiff::at (xd), u);
*grad_out = grad_tmp;
} else {
u = opt_fnd (xd);
}
return u. val ();
}
int main ()
{
Eigen::VectorXd x ( 5 );
x << 1 , 2 , 3 , 4 , 5 ;
bool success = optim::bfgs (x, opt_fn, nullptr );
if (success) {
std::cout << " bfgs: forward-mode autodiff test completed successfully. n " << std::endl;
} else {
std::cout << " bfgs: forward-mode autodiff test completed unsuccessfully. n " << std::endl;
}
std::cout << " solution: x = n " << x << std::endl;
return 0 ;
}Compiler avec:
g++ -Wall -std=c++17 -O3 -march=native -ffp-contract=fast -I/path/to/eigen -I/path/to/autodiff -I/path/to/optim/include optim_autodiff_ex.cpp -o optim_autodiff_ex.out -L/path/to/optim/lib -loptimVoir la documentation pour plus de détails sur ce sujet.
Keith O'Hara
Apache version 2