Optimlibは、非線形関数の数値最適化方法の軽量C ++ライブラリです。
特徴:
float )または二重精度( double )ライブラリとして利用可能。現在利用可能なアルゴリズムのリストには以下が含まれます。
完全なドキュメントはオンラインで入手できます:
ドキュメントのPDFバージョンはこちらから入手できます。
Optimlib APIは比較的単純な慣習に従います。ほとんどのアルゴリズムは次の方法で呼び出されます。
algorithm_id(<initial/final values>, <objective function>, <objective function data>);
順番に入力は次のとおりです。
たとえば、BFGSアルゴリズムは使用と呼ばれます
bfgs (ColVec_t& init_out_vals, std::function< double ( const ColVec_t& vals_inp, ColVec_t* grad_out, void * opt_data)> opt_objfn, void* opt_data);ここで、 ColVec_t 、例えば、 arma::vecまたはEigen::VectorXdタイプを表すために使用されます。
Optimlibは、Unix-Alike Systemsのみ(人気のLinuxベースのディストリビューション、およびMACO)のために、コンパイルされた共有ライブラリ、またはヘッダーのみのライブラリとして利用できます。 MSVCの有無にかかわらず、Windowsベースのシステムでこのライブラリを使用することはサポートされていません。
Optimlibには、ArmadilloまたはEigen C ++線形代数ライブラリのいずれかが必要です。 (Eigenバージョン3.4.0には、C ++ 14互換性のあるコンパイラが必要であることに注意してください。)
ヘッダーファイルを含める前に、次のいずれかを定義します。
# define OPTIM_ENABLE_ARMA_WRAPPERS
# define OPTIM_ENABLE_EIGEN_WRAPPERS例:
# define OPTIM_ENABLE_EIGEN_WRAPPERS
# include " optim.hpp "ライブラリは、標準./configure && make Methodを介してUnix-Alikeシステムにインストールできます。
最初にライブラリと必要なサブモジュールをクローンします。
# clone optim into the current directory
git clone https://github.com/kthohr/optim ./optim
# change directory
cd ./optim
# clone necessary submodules
git submodule update --init configureを実行する前に、次の環境変数の1つを設定します。
export ARMA_INCLUDE_PATH=/path/to/armadillo
export EIGEN_INCLUDE_PATH=/path/to/eigenついに:
# build and install with Eigen
./configure -i " /usr/local " -l eigen -p
make
make install最終コマンドは/usr/localにoptimlibをインストールします。
構成オプション( ./configure -hを参照):
主要な
-hヘルプを印刷します-iインストールパス。デフォルト:ビルドディレクトリ-fフローティングポイント精度モード。デフォルト: double-l線形代数ライブラリの選択を指定します。 armaまたはeigenを選択します-mリンクするBlasおよびLapackライブラリを指定します。たとえば、 -m "-lopenblas"または-m "-framework Accelerate"-oコンパイラ最適化オプション。デフォルトは-O3 -march=native -ffp-contract=fast -flto -DARMA_NO_DEBUGになります-p OpenMPの並列化機能を有効にする(推奨)二次
-cカバレッジビルド(Codecovで使用)-d 「開発」ビルド-gデバッグビルド( -O0 -gに設定された最適化フラグ)特別
--header-only-version Optimlibのヘッダーのみのバージョンを生成します(以下を参照) Optimlibは、ヘッダーのみのライブラリとしても利用できます(つまり、共有ライブラリをコンパイルする必要はありません)。 --header-only-versionオプションでconfigure実行するだけです。
./configure --header-only-versionこれにより、optimlibのコピーを含む新しいディレクトリheader_only_versionが作成され、インラインベースで動作するように変更されます。このヘッダーのみのバージョンを使用すると、ヘッダーファイル( #include "optim.hpp )を含めて、 head_only_versionディレクトリ(例、 -I/path/to/optimlib/header_only_version )へのパスを設定します。
rパッケージを備えたOptimlibを使用するには、最初にライブラリのヘッダーのみのバージョンを生成します(上記参照)。次に、OptimLibファイルを含める前に、コンパイラ定義を追加するだけです。
# define OPTIM_USE_RCPP_ARMADILLO
# include " optim.hpp "# define OPTIM_USE_RCPP_EIGEN
# include " optim.hpp " 職場でのOptimlibを説明するには、Ackley関数のグローバルな最小値を検索することを検討してください。
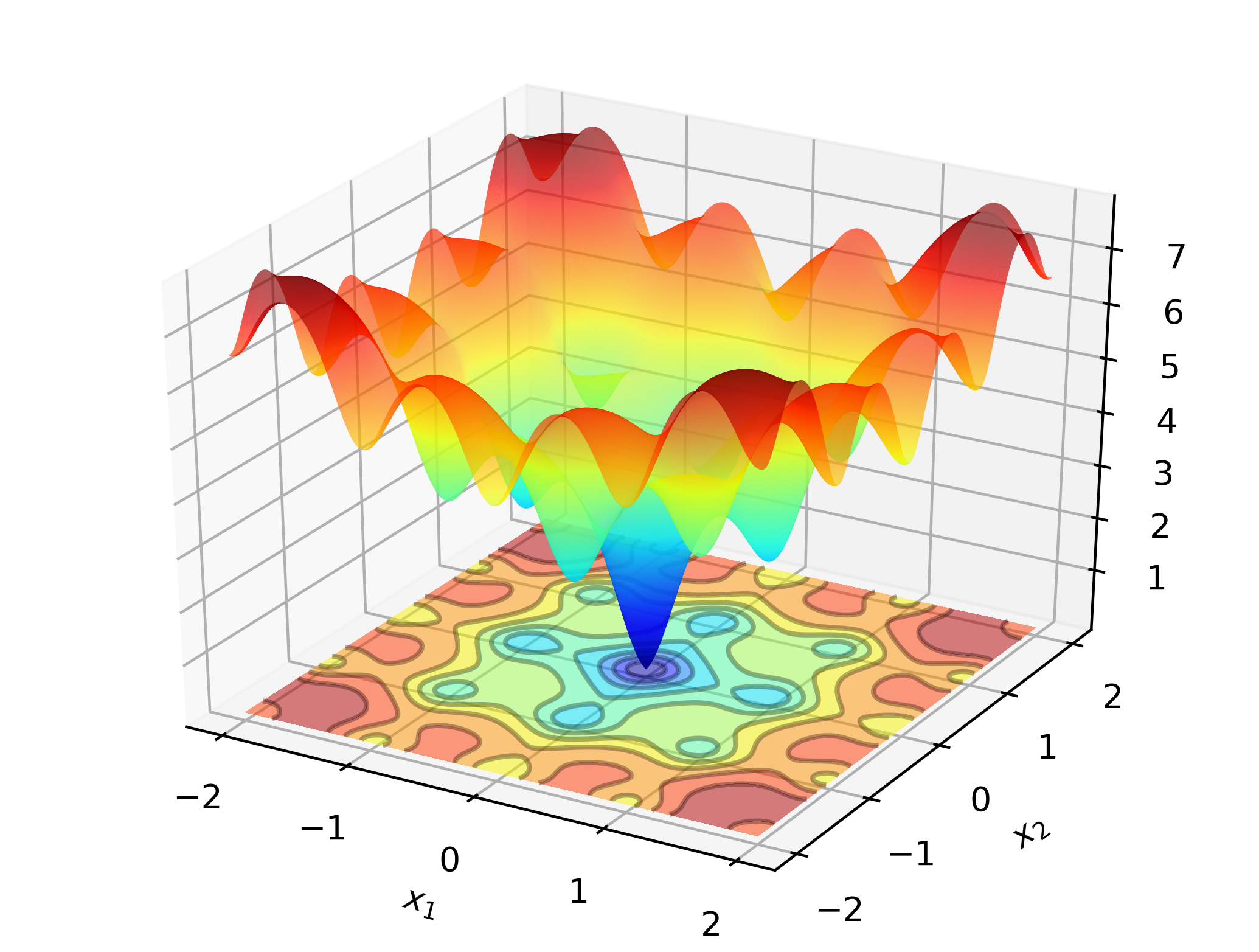
これは、多くの局所的な最小値を備えたよく知られているテスト機能です。ニュートン型メソッド(BFGなど)は、初期値の選択に敏感であり、ここではかなり不十分に機能します。そのため、グローバル検索方法を採用します - このケースでは、微分進化です。
コード:
# define OPTIM_ENABLE_EIGEN_WRAPPERS
# include " optim.hpp "
# define OPTIM_PI 3.14159265358979
double
ackley_fn ( const Eigen::VectorXd& vals_inp, Eigen::VectorXd* grad_out, void * opt_data)
{
const double x = vals_inp ( 0 );
const double y = vals_inp ( 1 );
const double obj_val = 20 + std::exp ( 1 ) - 20 * std::exp ( - 0.2 * std::sqrt ( 0.5 *(x*x + y*y)) ) - std::exp ( 0.5 *( std::cos ( 2 * OPTIM_PI * x) + std::cos ( 2 * OPTIM_PI * y)) );
return obj_val;
}
int main ()
{
Eigen::VectorXd x = 2.0 * Eigen::VectorXd::Ones ( 2 ); // initial values: (2,2)
bool success = optim::de (x, ackley_fn, nullptr );
if (success) {
std::cout << " de: Ackley test completed successfully. " << std::endl;
} else {
std::cout << " de: Ackley test completed unsuccessfully. " << std::endl;
}
std::cout << " de: solution to Ackley test: n " << x << std::endl;
return 0 ;
}X86ベースのコンピューターでは、この例を使用してコンパイルできます。
g++ -Wall -std=c++14 -O3 -march=native -ffp-contract=fast -I/path/to/eigen -I/path/to/optim/include optim_de_ex.cpp -o optim_de_ex.out -L/path/to/optim/lib -loptim出力:
de: Ackley test completed successfully.
elapsed time: 0.028167s
de: solution to Ackley test:
-1.2702e-17
-3.8432e-16
標準のラップトップでは、OptimLibは、1秒のほんの一部でマシン内の正確なソリューションを計算します。
この例のアルマジロベースのバージョン:
# define OPTIM_ENABLE_ARMA_WRAPPERS
# include " optim.hpp "
# define OPTIM_PI 3.14159265358979
double
ackley_fn ( const arma::vec& vals_inp, arma::vec* grad_out, void * opt_data)
{
const double x = vals_inp ( 0 );
const double y = vals_inp ( 1 );
const double obj_val = 20 + std::exp ( 1 ) - 20 * std::exp ( - 0.2 * std::sqrt ( 0.5 *(x*x + y*y)) ) - std::exp ( 0.5 *( std::cos ( 2 * OPTIM_PI * x) + std::cos ( 2 * OPTIM_PI * y)) );
return obj_val;
}
int main ()
{
arma::vec x = arma::ones ( 2 , 1 ) + 1.0 ; // initial values: (2,2)
bool success = optim::de (x, ackley_fn, nullptr );
if (success) {
std::cout << " de: Ackley test completed successfully. " << std::endl;
} else {
std::cout << " de: Ackley test completed unsuccessfully. " << std::endl;
}
arma::cout << " de: solution to Ackley test: n " << x << arma::endl;
return 0 ;
}コンパイルと実行:
g++ -Wall -std=c++11 -O3 -march=native -ffp-contract=fast -I/path/to/armadillo -I/path/to/optim/include optim_de_ex.cpp -o optim_de_ex.out -L/path/to/optim/lib -loptim
./optim_de_ex.out追加の例については、 /testsディレクトリとhttps://optimlib.readthedocs.io/en/latest/各アルゴリズムの詳細な説明を確認してください。
データベースの例については、統計と機械学習で一般的なロジットモデルの最尤推定を検討してください。この場合、勾配とヘシアンの閉じた式式があります。一般的な勾配降下法であるAdam(適応モーメント推定)を採用し、純粋なニュートンベースのアルゴリズムと比較します。
# define OPTIM_ENABLE_ARMA_WRAPPERS
# include " optim.hpp "
// sigmoid function
inline
arma::mat sigm ( const arma::mat& X)
{
return 1.0 / ( 1.0 + arma::exp (-X));
}
// log-likelihood function data
struct ll_data_t
{
arma::vec Y;
arma::mat X;
};
// log-likelihood function with hessian
double ll_fn_whess ( const arma::vec& vals_inp, arma::vec* grad_out, arma::mat* hess_out, void * opt_data)
{
ll_data_t * objfn_data = reinterpret_cast < ll_data_t *>(opt_data);
arma::vec Y = objfn_data-> Y ;
arma::mat X = objfn_data-> X ;
arma::vec mu = sigm (X*vals_inp);
const double norm_term = static_cast < double >(Y. n_elem );
const double obj_val = - arma::accu ( Y% arma::log (mu) + ( 1.0 -Y)% arma::log ( 1.0 -mu) ) / norm_term;
//
if (grad_out)
{
*grad_out = X. t () * (mu - Y) / norm_term;
}
//
if (hess_out)
{
arma::mat S = arma::diagmat ( mu%( 1.0 -mu) );
*hess_out = X. t () * S * X / norm_term;
}
//
return obj_val;
}
// log-likelihood function for Adam
double ll_fn ( const arma::vec& vals_inp, arma::vec* grad_out, void * opt_data)
{
return ll_fn_whess (vals_inp,grad_out, nullptr ,opt_data);
}
//
int main ()
{
int n_dim = 5 ; // dimension of parameter vector
int n_samp = 4000 ; // sample length
arma::mat X = arma::randn (n_samp,n_dim);
arma::vec theta_0 = 1.0 + 3.0 * arma::randu (n_dim, 1 );
arma::vec mu = sigm (X*theta_0);
arma::vec Y (n_samp);
for ( int i= 0 ; i < n_samp; i++)
{
Y (i) = ( arma::as_scalar ( arma::randu ( 1 )) < mu (i) ) ? 1.0 : 0.0 ;
}
// fn data and initial values
ll_data_t opt_data;
opt_data. Y = std::move (Y);
opt_data. X = std::move (X);
arma::vec x = arma::ones (n_dim, 1 ) + 1.0 ; // initial values
// run Adam-based optim
optim:: algo_settings_t settings;
settings. gd_method = 6 ;
settings. gd_settings . step_size = 0.1 ;
std::chrono::time_point<std::chrono::system_clock> start = std::chrono::system_clock::now ();
bool success = optim::gd (x,ll_fn,&opt_data,settings);
std::chrono::time_point<std::chrono::system_clock> end = std::chrono::system_clock::now ();
std::chrono::duration< double > elapsed_seconds = end-start;
//
if (success) {
std::cout << " Adam: logit_reg test completed successfully. n "
<< " elapsed time: " << elapsed_seconds. count () << " s n " ;
} else {
std::cout << " Adam: logit_reg test completed unsuccessfully. " << std::endl;
}
arma::cout << " n Adam: true values vs estimates: n " << arma::join_rows (theta_0,x) << arma::endl;
//
// run Newton-based optim
x = arma::ones (n_dim, 1 ) + 1.0 ; // initial values
start = std::chrono::system_clock::now ();
success = optim::newton (x,ll_fn_whess,&opt_data);
end = std::chrono::system_clock::now ();
elapsed_seconds = end-start;
//
if (success) {
std::cout << " newton: logit_reg test completed successfully. n "
<< " elapsed time: " << elapsed_seconds. count () << " s n " ;
} else {
std::cout << " newton: logit_reg test completed unsuccessfully. " << std::endl;
}
arma::cout << " n newton: true values vs estimates: n " << arma::join_rows (theta_0,x) << arma::endl;
return 0 ;
}出力:
Adam: logit_reg test completed successfully.
elapsed time: 0.025128s
Adam: true values vs estimates:
2.7850 2.6993
3.6561 3.6798
2.3379 2.3860
2.3167 2.4313
2.2465 2.3064
newton: logit_reg test completed successfully.
elapsed time: 0.255909s
newton: true values vs estimates:
2.7850 2.6993
3.6561 3.6798
2.3379 2.3860
2.3167 2.4313
2.2465 2.3064
EigenとAutodiff Libraryを組み合わせることにより、OptimLibは自動分化の実験的サポートを提供します。
球機能のBFGを使用したフォワードモードの自動分化を使用する例:
# define OPTIM_ENABLE_EIGEN_WRAPPERS
# include " optim.hpp "
# include < autodiff/forward/real.hpp >
# include < autodiff/forward/real/eigen.hpp >
//
autodiff::real
opt_fnd ( const autodiff::ArrayXreal& x)
{
return x. cwiseProduct (x). sum ();
}
double
opt_fn ( const Eigen::VectorXd& x, Eigen::VectorXd* grad_out, void * opt_data)
{
autodiff::real u;
autodiff::ArrayXreal xd = x. eval ();
if (grad_out) {
Eigen::VectorXd grad_tmp = autodiff::gradient (opt_fnd, autodiff::wrt (xd), autodiff::at (xd), u);
*grad_out = grad_tmp;
} else {
u = opt_fnd (xd);
}
return u. val ();
}
int main ()
{
Eigen::VectorXd x ( 5 );
x << 1 , 2 , 3 , 4 , 5 ;
bool success = optim::bfgs (x, opt_fn, nullptr );
if (success) {
std::cout << " bfgs: forward-mode autodiff test completed successfully. n " << std::endl;
} else {
std::cout << " bfgs: forward-mode autodiff test completed unsuccessfully. n " << std::endl;
}
std::cout << " solution: x = n " << x << std::endl;
return 0 ;
}コンパイル:
g++ -Wall -std=c++17 -O3 -march=native -ffp-contract=fast -I/path/to/eigen -I/path/to/autodiff -I/path/to/optim/include optim_autodiff_ex.cpp -o optim_autodiff_ex.out -L/path/to/optim/lib -loptimこのトピックの詳細については、ドキュメントを参照してください。
キース・オハラ
Apacheバージョン2