Optimlib ist eine leichte C ++ - Bibliothek mit numerischen Optimierungsmethoden für nichtlineare Funktionen.
Merkmale:
float ) oder doppelte Präzisionsbibliothek ( double ) Bibliothek.Eine Liste der derzeit verfügbaren Algorithmen umfasst:
Vollständige Dokumentation ist online verfügbar:
Eine PDF -Version der Dokumentation ist hier verfügbar.
Die Optimlib -API folgt einer relativ einfachen Konvention, wobei die meisten Algorithmen folgendermaßen aufgerufen werden:
algorithm_id(<initial/final values>, <objective function>, <objective function data>);
Die Eingaben sind in der Reihenfolge:
Zum Beispiel wird der BFGS -Algorithmus aufgerufen
bfgs (ColVec_t& init_out_vals, std::function< double ( const ColVec_t& vals_inp, ColVec_t* grad_out, void * opt_data)> opt_objfn, void* opt_data); Wo ColVec_t verwendet wird, um darzustellen, z. B. arma::vec oder Eigen::VectorXd -Typen.
Optimlib ist als zusammengestellte gemeinsame Bibliothek oder als nur für Unix-Alike-Systeme (z. B. beliebte Linux-basierte Distributiere sowie MacOS) erhältlich. Die Verwendung dieser Bibliothek mit Windows-basierten Systemen mit oder ohne MSVC wird nicht unterstützt .
Optimlib benötigt entweder die linearen Algebra -Algebra -Bibliotheken von Eigenschaft oder Eigen. (Beachten Sie, dass Eigenversion 3.4.0 einen c ++ 14-kompatiblen Compiler erfordert.)
Definieren Sie vor der Einbeziehung der Header -Dateien eine der folgenden:
# define OPTIM_ENABLE_ARMA_WRAPPERS
# define OPTIM_ENABLE_EIGEN_WRAPPERSBeispiel:
# define OPTIM_ENABLE_EIGEN_WRAPPERS
# include " optim.hpp " Die Bibliothek kann über die Standard-Systeme auf Unix-Alike-Systemen installiert werden ./configure && make Methode.
Zuerst klonen Sie die Bibliothek und alle notwendigen Submodule:
# clone optim into the current directory
git clone https://github.com/kthohr/optim ./optim
# change directory
cd ./optim
# clone necessary submodules
git submodule update --init Setzen Sie (eins) der folgenden Umgebungsvariablen, bevor Sie configure ausführen:
export ARMA_INCLUDE_PATH=/path/to/armadillo
export EIGEN_INCLUDE_PATH=/path/to/eigenEndlich:
# build and install with Eigen
./configure -i " /usr/local " -l eigen -p
make
make install Der endgültige Befehl installiert Optimlib in /usr/local .
Konfigurationsoptionen (siehe ./configure -h ):
Primär
-h Druckhilfe-i Installationspfad; Standard: Das Build -Verzeichnis-f Floating-Punkt-Präzisionsmodus; Standard: double-l Geben Sie die Auswahl der linearen Algebra -Bibliothek an; Wählen Sie arma oder eigen-m Geben Sie die BLAS- und LAPACK -Bibliotheken an, mit denen Sie verknüpfen sollen; Zum Beispiel -m "-lopenblas" oder -m "-framework Accelerate"-o Compiler -Optimierungsoptionen; Standardeinstellungen zu -O3 -march=native -ffp-contract=fast -flto -DARMA_NO_DEBUG-p Aktivieren Sie die OpenMP -Parallelisierungsfunktionen ( empfohlen )Sekundär
-c Ein Deckungsbau (mit Codecov verwendet)-d Ein "Entwicklung" -Build-g Ein Debugging -Build (Optimierungsflags auf -O0 -g eingestellt)Besonders
--header-only-version generieren eine Nur-Header-Version von Optimlib (siehe unten) Optimlib ist auch als Learle-Bibliothek erhältlich (dh ohne eine gemeinsame Bibliothek zusammenzustellen). Führen Sie einfach configure mit der Option --header-only-version aus:
./configure --header-only-version Dadurch wird ein neues Verzeichnis erstellt, header_only_version , das eine Kopie von Optimlib enthält, die so geändert wird, dass sie auf einer Inline -Basis arbeiten. Geben Sie mit dieser nur Header -Version einfach die Header -Dateien ( #include "optim.hpp ) ein und setzen Sie den Pfad in das Verzeichnis head_only_version (z. B. -I/path/to/optimlib/header_only_version ).
Um Optimlib mit einem R-Paket zu verwenden, generieren Sie zunächst eine nur Header-Version der Bibliothek (siehe oben). Fügen Sie dann einfach eine Compiler -Definition hinzu, bevor Sie die Optimlib -Dateien einbeziehen.
# define OPTIM_USE_RCPP_ARMADILLO
# include " optim.hpp "# define OPTIM_USE_RCPP_EIGEN
# include " optim.hpp " Um Optimlib bei der Arbeit zu veranschaulichen, sollten Sie nach dem globalen Minimum der Ackley -Funktion suchen:
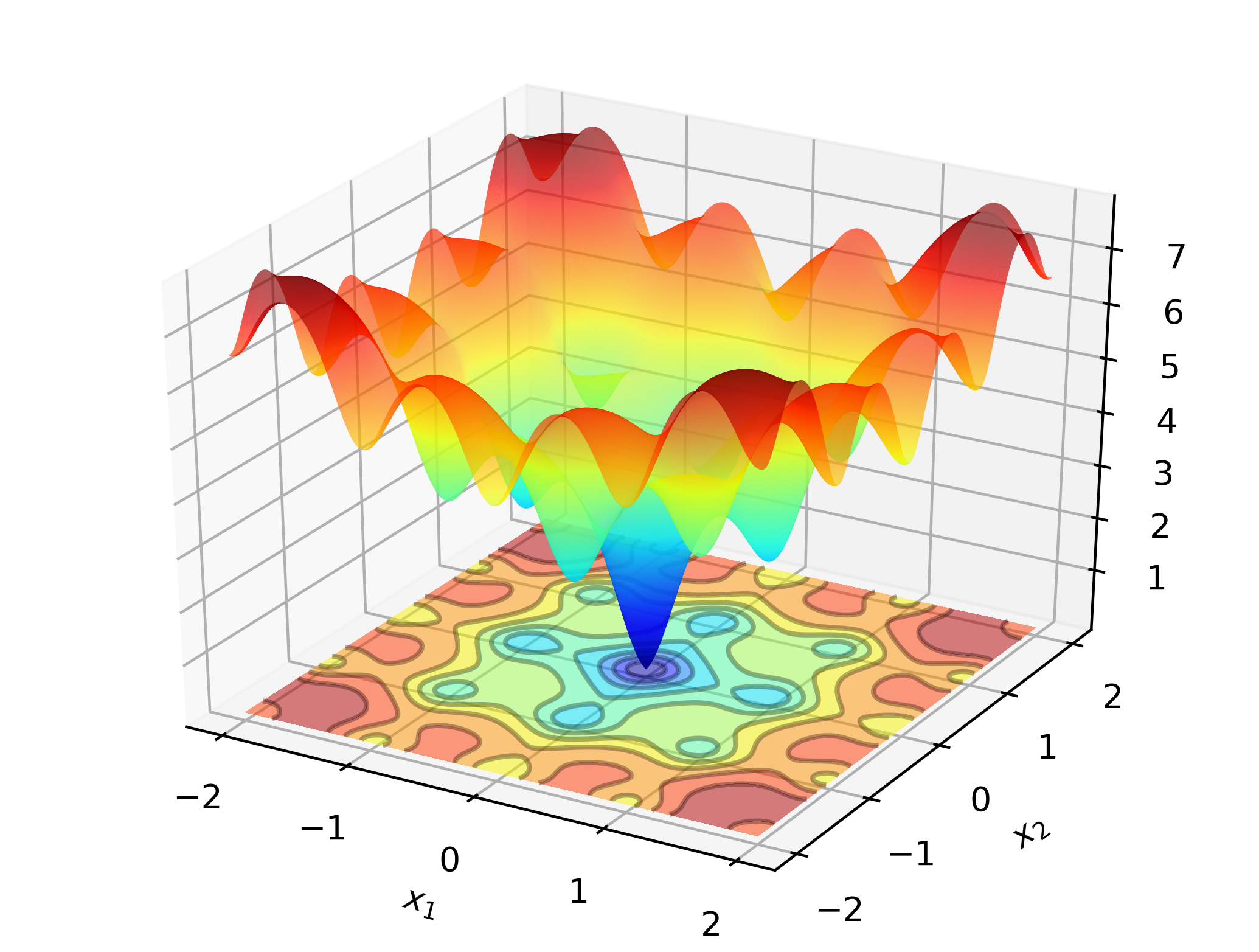
Dies ist eine bekannte Testfunktion mit vielen lokalen Minima. Newton-Typ-Methoden (wie BFGs) sind empfindlich gegenüber der Auswahl der Anfangswerte und werden hier ziemlich schlecht abschneiden. Daher werden wir eine globale Suchmethode anwenden-in diesem Fall: Differentialentwicklung.
Code:
# define OPTIM_ENABLE_EIGEN_WRAPPERS
# include " optim.hpp "
# define OPTIM_PI 3.14159265358979
double
ackley_fn ( const Eigen::VectorXd& vals_inp, Eigen::VectorXd* grad_out, void * opt_data)
{
const double x = vals_inp ( 0 );
const double y = vals_inp ( 1 );
const double obj_val = 20 + std::exp ( 1 ) - 20 * std::exp ( - 0.2 * std::sqrt ( 0.5 *(x*x + y*y)) ) - std::exp ( 0.5 *( std::cos ( 2 * OPTIM_PI * x) + std::cos ( 2 * OPTIM_PI * y)) );
return obj_val;
}
int main ()
{
Eigen::VectorXd x = 2.0 * Eigen::VectorXd::Ones ( 2 ); // initial values: (2,2)
bool success = optim::de (x, ackley_fn, nullptr );
if (success) {
std::cout << " de: Ackley test completed successfully. " << std::endl;
} else {
std::cout << " de: Ackley test completed unsuccessfully. " << std::endl;
}
std::cout << " de: solution to Ackley test: n " << x << std::endl;
return 0 ;
}Auf X86-basierten Computern kann dieses Beispiel mit: zusammengestellt werden:
g++ -Wall -std=c++14 -O3 -march=native -ffp-contract=fast -I/path/to/eigen -I/path/to/optim/include optim_de_ex.cpp -o optim_de_ex.out -L/path/to/optim/lib -loptimAusgabe:
de: Ackley test completed successfully.
elapsed time: 0.028167s
de: solution to Ackley test:
-1.2702e-17
-3.8432e-16
Bei einem Standard -Laptop berechnet Optimlib eine Lösung für die Maschinenpräzision in einem Bruchteil einer Sekunde.
Die armadillo-basierte Version dieses Beispiels:
# define OPTIM_ENABLE_ARMA_WRAPPERS
# include " optim.hpp "
# define OPTIM_PI 3.14159265358979
double
ackley_fn ( const arma::vec& vals_inp, arma::vec* grad_out, void * opt_data)
{
const double x = vals_inp ( 0 );
const double y = vals_inp ( 1 );
const double obj_val = 20 + std::exp ( 1 ) - 20 * std::exp ( - 0.2 * std::sqrt ( 0.5 *(x*x + y*y)) ) - std::exp ( 0.5 *( std::cos ( 2 * OPTIM_PI * x) + std::cos ( 2 * OPTIM_PI * y)) );
return obj_val;
}
int main ()
{
arma::vec x = arma::ones ( 2 , 1 ) + 1.0 ; // initial values: (2,2)
bool success = optim::de (x, ackley_fn, nullptr );
if (success) {
std::cout << " de: Ackley test completed successfully. " << std::endl;
} else {
std::cout << " de: Ackley test completed unsuccessfully. " << std::endl;
}
arma::cout << " de: solution to Ackley test: n " << x << arma::endl;
return 0 ;
}Kompilieren und rennen:
g++ -Wall -std=c++11 -O3 -march=native -ffp-contract=fast -I/path/to/armadillo -I/path/to/optim/include optim_de_ex.cpp -o optim_de_ex.out -L/path/to/optim/lib -loptim
./optim_de_ex.out Weitere Beispiele finden Sie im Verzeichnis /tests .
Betrachten Sie für ein datenbasiertes Beispiel die maximale Wahrscheinlichkeitsschätzung eines Logit-Modells, das in Statistiken und maschinellem Lernen häufig ist. In diesem Fall haben wir geschlossene Ausdrücke für den Gradienten und Hessischen. Wir werden eine beliebte Gradientenabstiegsmethode, Adam (adaptive Momentschätzung), anwenden und mit einem reinen Newton-basierten Algorithmus vergleichen.
# define OPTIM_ENABLE_ARMA_WRAPPERS
# include " optim.hpp "
// sigmoid function
inline
arma::mat sigm ( const arma::mat& X)
{
return 1.0 / ( 1.0 + arma::exp (-X));
}
// log-likelihood function data
struct ll_data_t
{
arma::vec Y;
arma::mat X;
};
// log-likelihood function with hessian
double ll_fn_whess ( const arma::vec& vals_inp, arma::vec* grad_out, arma::mat* hess_out, void * opt_data)
{
ll_data_t * objfn_data = reinterpret_cast < ll_data_t *>(opt_data);
arma::vec Y = objfn_data-> Y ;
arma::mat X = objfn_data-> X ;
arma::vec mu = sigm (X*vals_inp);
const double norm_term = static_cast < double >(Y. n_elem );
const double obj_val = - arma::accu ( Y% arma::log (mu) + ( 1.0 -Y)% arma::log ( 1.0 -mu) ) / norm_term;
//
if (grad_out)
{
*grad_out = X. t () * (mu - Y) / norm_term;
}
//
if (hess_out)
{
arma::mat S = arma::diagmat ( mu%( 1.0 -mu) );
*hess_out = X. t () * S * X / norm_term;
}
//
return obj_val;
}
// log-likelihood function for Adam
double ll_fn ( const arma::vec& vals_inp, arma::vec* grad_out, void * opt_data)
{
return ll_fn_whess (vals_inp,grad_out, nullptr ,opt_data);
}
//
int main ()
{
int n_dim = 5 ; // dimension of parameter vector
int n_samp = 4000 ; // sample length
arma::mat X = arma::randn (n_samp,n_dim);
arma::vec theta_0 = 1.0 + 3.0 * arma::randu (n_dim, 1 );
arma::vec mu = sigm (X*theta_0);
arma::vec Y (n_samp);
for ( int i= 0 ; i < n_samp; i++)
{
Y (i) = ( arma::as_scalar ( arma::randu ( 1 )) < mu (i) ) ? 1.0 : 0.0 ;
}
// fn data and initial values
ll_data_t opt_data;
opt_data. Y = std::move (Y);
opt_data. X = std::move (X);
arma::vec x = arma::ones (n_dim, 1 ) + 1.0 ; // initial values
// run Adam-based optim
optim:: algo_settings_t settings;
settings. gd_method = 6 ;
settings. gd_settings . step_size = 0.1 ;
std::chrono::time_point<std::chrono::system_clock> start = std::chrono::system_clock::now ();
bool success = optim::gd (x,ll_fn,&opt_data,settings);
std::chrono::time_point<std::chrono::system_clock> end = std::chrono::system_clock::now ();
std::chrono::duration< double > elapsed_seconds = end-start;
//
if (success) {
std::cout << " Adam: logit_reg test completed successfully. n "
<< " elapsed time: " << elapsed_seconds. count () << " s n " ;
} else {
std::cout << " Adam: logit_reg test completed unsuccessfully. " << std::endl;
}
arma::cout << " n Adam: true values vs estimates: n " << arma::join_rows (theta_0,x) << arma::endl;
//
// run Newton-based optim
x = arma::ones (n_dim, 1 ) + 1.0 ; // initial values
start = std::chrono::system_clock::now ();
success = optim::newton (x,ll_fn_whess,&opt_data);
end = std::chrono::system_clock::now ();
elapsed_seconds = end-start;
//
if (success) {
std::cout << " newton: logit_reg test completed successfully. n "
<< " elapsed time: " << elapsed_seconds. count () << " s n " ;
} else {
std::cout << " newton: logit_reg test completed unsuccessfully. " << std::endl;
}
arma::cout << " n newton: true values vs estimates: n " << arma::join_rows (theta_0,x) << arma::endl;
return 0 ;
}Ausgabe:
Adam: logit_reg test completed successfully.
elapsed time: 0.025128s
Adam: true values vs estimates:
2.7850 2.6993
3.6561 3.6798
2.3379 2.3860
2.3167 2.4313
2.2465 2.3064
newton: logit_reg test completed successfully.
elapsed time: 0.255909s
newton: true values vs estimates:
2.7850 2.6993
3.6561 3.6798
2.3379 2.3860
2.3167 2.4313
2.2465 2.3064
Durch die Kombination von Eigen mit der Autodiff -Bibliothek bietet Optimlib experimentelle Unterstützung für die automatische Differenzierung.
Beispiel unter Verwendung der automatischen Differenzierung von Vorwärtsmodus mit BFGs für die Sphere-Funktion:
# define OPTIM_ENABLE_EIGEN_WRAPPERS
# include " optim.hpp "
# include < autodiff/forward/real.hpp >
# include < autodiff/forward/real/eigen.hpp >
//
autodiff::real
opt_fnd ( const autodiff::ArrayXreal& x)
{
return x. cwiseProduct (x). sum ();
}
double
opt_fn ( const Eigen::VectorXd& x, Eigen::VectorXd* grad_out, void * opt_data)
{
autodiff::real u;
autodiff::ArrayXreal xd = x. eval ();
if (grad_out) {
Eigen::VectorXd grad_tmp = autodiff::gradient (opt_fnd, autodiff::wrt (xd), autodiff::at (xd), u);
*grad_out = grad_tmp;
} else {
u = opt_fnd (xd);
}
return u. val ();
}
int main ()
{
Eigen::VectorXd x ( 5 );
x << 1 , 2 , 3 , 4 , 5 ;
bool success = optim::bfgs (x, opt_fn, nullptr );
if (success) {
std::cout << " bfgs: forward-mode autodiff test completed successfully. n " << std::endl;
} else {
std::cout << " bfgs: forward-mode autodiff test completed unsuccessfully. n " << std::endl;
}
std::cout << " solution: x = n " << x << std::endl;
return 0 ;
}Kompilieren mit:
g++ -Wall -std=c++17 -O3 -march=native -ffp-contract=fast -I/path/to/eigen -I/path/to/autodiff -I/path/to/optim/include optim_autodiff_ex.cpp -o optim_autodiff_ex.out -L/path/to/optim/lib -loptimWeitere Informationen zu diesem Thema finden Sie in der Dokumentation.
Keith O'Hara
Apache Version 2