Optimlib es una biblioteca liviana de C ++ de métodos de optimización numérica para funciones no lineales.
Características:
float ) o doble precisión ( double ).Una lista de algoritmos disponibles actualmente incluye:
La documentación completa está disponible en línea:
Una versión PDF de la documentación está disponible aquí.
La API de Optimlib sigue una convención relativamente simple, con la mayoría de los algoritmos llamados de la siguiente manera:
algorithm_id(<initial/final values>, <objective function>, <objective function data>);
Las entradas, en orden, son:
Por ejemplo, el algoritmo BFGS se llama usar
bfgs (ColVec_t& init_out_vals, std::function< double ( const ColVec_t& vals_inp, ColVec_t* grad_out, void * opt_data)> opt_objfn, void* opt_data); donde se usa ColVec_t para representar, por ejemplo, arma::vec o Eigen::VectorXd tipos.
Optimlib está disponible como una biblioteca compartida compilada, o como biblioteca solo de encabezado, solo para sistemas UNIX-alike (por ejemplo, distribuciones populares basadas en Linux, así como macOS). El uso de esta biblioteca con sistemas basados en Windows, con o sin MSVC, no es compatible .
Optimlib requiere las bibliotecas Armadillo o Eigen C ++ Linear Algebra. (Tenga en cuenta que Eigen versión 3.4.0 requiere un compilador C ++ 14 compatible).
Antes de incluir los archivos de encabezado, defina uno de los siguientes:
# define OPTIM_ENABLE_ARMA_WRAPPERS
# define OPTIM_ENABLE_EIGEN_WRAPPERSEjemplo:
# define OPTIM_ENABLE_EIGEN_WRAPPERS
# include " optim.hpp " La biblioteca se puede instalar en sistemas UNIX-alike a través del método estándar ./configure && make .
Primer clon de la biblioteca y los submódulos necesarios:
# clone optim into the current directory
git clone https://github.com/kthohr/optim ./optim
# change directory
cd ./optim
# clone necessary submodules
git submodule update --init Establecer (una) de las siguientes variables de entorno antes de ejecutar configure :
export ARMA_INCLUDE_PATH=/path/to/armadillo
export EIGEN_INCLUDE_PATH=/path/to/eigenFinalmente:
# build and install with Eigen
./configure -i " /usr/local " -l eigen -p
make
make install El comando final instalará Optimlib en /usr/local .
Opciones de configuración (ver ./configure -h ):
Primario
-h Ayuda de impresión-i ruta de instalación; Valor predeterminado: el directorio de compilación-f Modo de precisión de punto flotante; Valor predeterminado: double-l especificar la elección de la biblioteca de álgebra lineal; Elija arma o eigen-m especifique las bibliotecas BLAS y LAPACK para vincular; Por ejemplo, -m "-lopenblas" o -m "-framework Accelerate"-o Opciones de optimización del compilador; El valor predeterminado a -O3 -march=native -ffp-contract=fast -flto -DARMA_NO_DEBUG-p habilitar las características de paralelización de OpenMP ( recomendado )Secundario
-c una construcción de cobertura (utilizada con CodeCov)-d una construcción de 'desarrollo'-g una compilación de depuración (indicadores de optimización establecidos en -O0 -g )Especial
--header-only-version Genere una versión solo de encabezado de Optimlib (ver más abajo) Optimlib también está disponible como una biblioteca solo de encabezado (es decir, sin la necesidad de compilar una biblioteca compartida). Simplemente ejecute configure con la opción --header-only-version :
./configure --header-only-version Esto creará un nuevo directorio, header_only_version , que contiene una copia de Optimlib, modificada para trabajar en línea. Con esta versión de solo encabezado, simplemente incluya los archivos de encabezado ( #include "optim.hpp ) y establezca la ruta de inclusión en el directorio head_only_version (por ejemplo, -I/path/to/optimlib/header_only_version ).
Para usar Optimlib con un paquete R, primero genere una versión solo de encabezado de la biblioteca (ver arriba). Luego, simplemente agregue una definición del compilador antes de incluir los archivos OptimLib.
# define OPTIM_USE_RCPP_ARMADILLO
# include " optim.hpp "# define OPTIM_USE_RCPP_EIGEN
# include " optim.hpp " Para ilustrar Optimlib en el trabajo, considere buscar el mínimo global de la función Ackley:
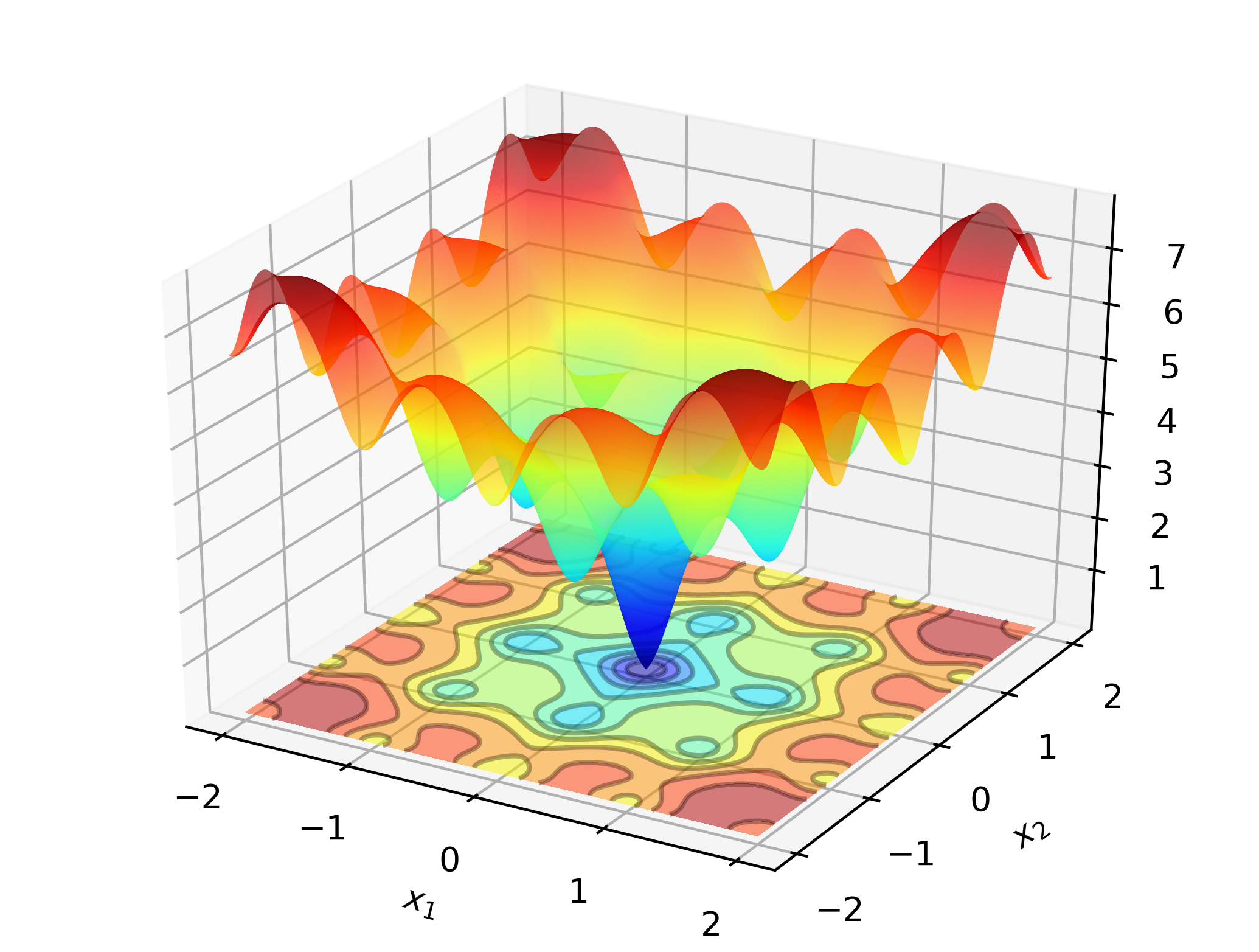
Esta es una función de prueba bien conocida con muchos mínimos locales. Los métodos de tipo Newton (como los BFG) son sensibles a la elección de los valores iniciales y funcionarán bastante mal aquí. Como tal, emplearemos un método de búsqueda global, en este caso: evolución diferencial.
Código:
# define OPTIM_ENABLE_EIGEN_WRAPPERS
# include " optim.hpp "
# define OPTIM_PI 3.14159265358979
double
ackley_fn ( const Eigen::VectorXd& vals_inp, Eigen::VectorXd* grad_out, void * opt_data)
{
const double x = vals_inp ( 0 );
const double y = vals_inp ( 1 );
const double obj_val = 20 + std::exp ( 1 ) - 20 * std::exp ( - 0.2 * std::sqrt ( 0.5 *(x*x + y*y)) ) - std::exp ( 0.5 *( std::cos ( 2 * OPTIM_PI * x) + std::cos ( 2 * OPTIM_PI * y)) );
return obj_val;
}
int main ()
{
Eigen::VectorXd x = 2.0 * Eigen::VectorXd::Ones ( 2 ); // initial values: (2,2)
bool success = optim::de (x, ackley_fn, nullptr );
if (success) {
std::cout << " de: Ackley test completed successfully. " << std::endl;
} else {
std::cout << " de: Ackley test completed unsuccessfully. " << std::endl;
}
std::cout << " de: solution to Ackley test: n " << x << std::endl;
return 0 ;
}En las computadoras basadas en X86, este ejemplo se puede compilar usando:
g++ -Wall -std=c++14 -O3 -march=native -ffp-contract=fast -I/path/to/eigen -I/path/to/optim/include optim_de_ex.cpp -o optim_de_ex.out -L/path/to/optim/lib -loptimProducción:
de: Ackley test completed successfully.
elapsed time: 0.028167s
de: solution to Ackley test:
-1.2702e-17
-3.8432e-16
En una computadora portátil estándar, Optimlib calculará una solución dentro de la precisión de la máquina en una fracción de segundo.
La versión basada en Armadillo de este ejemplo:
# define OPTIM_ENABLE_ARMA_WRAPPERS
# include " optim.hpp "
# define OPTIM_PI 3.14159265358979
double
ackley_fn ( const arma::vec& vals_inp, arma::vec* grad_out, void * opt_data)
{
const double x = vals_inp ( 0 );
const double y = vals_inp ( 1 );
const double obj_val = 20 + std::exp ( 1 ) - 20 * std::exp ( - 0.2 * std::sqrt ( 0.5 *(x*x + y*y)) ) - std::exp ( 0.5 *( std::cos ( 2 * OPTIM_PI * x) + std::cos ( 2 * OPTIM_PI * y)) );
return obj_val;
}
int main ()
{
arma::vec x = arma::ones ( 2 , 1 ) + 1.0 ; // initial values: (2,2)
bool success = optim::de (x, ackley_fn, nullptr );
if (success) {
std::cout << " de: Ackley test completed successfully. " << std::endl;
} else {
std::cout << " de: Ackley test completed unsuccessfully. " << std::endl;
}
arma::cout << " de: solution to Ackley test: n " << x << arma::endl;
return 0 ;
}Compilar y ejecutar:
g++ -Wall -std=c++11 -O3 -march=native -ffp-contract=fast -I/path/to/armadillo -I/path/to/optim/include optim_de_ex.cpp -o optim_de_ex.out -L/path/to/optim/lib -loptim
./optim_de_ex.out Consulte el directorio /tests para ver ejemplos adicionales y https://optimlib.readthedocs.io/en/latest/ para obtener una descripción detallada de cada algoritmo.
Para un ejemplo basado en datos, considere la estimación de máxima probabilidad de un modelo logit, común en estadísticas y aprendizaje automático. En este caso tenemos expresiones de forma cerrada para el gradiente y Hessian. Emplearemos un método de descenso de gradiente popular, Adam (estimación de momento adaptativo), y compararemos con un algoritmo puro con sede en Newton.
# define OPTIM_ENABLE_ARMA_WRAPPERS
# include " optim.hpp "
// sigmoid function
inline
arma::mat sigm ( const arma::mat& X)
{
return 1.0 / ( 1.0 + arma::exp (-X));
}
// log-likelihood function data
struct ll_data_t
{
arma::vec Y;
arma::mat X;
};
// log-likelihood function with hessian
double ll_fn_whess ( const arma::vec& vals_inp, arma::vec* grad_out, arma::mat* hess_out, void * opt_data)
{
ll_data_t * objfn_data = reinterpret_cast < ll_data_t *>(opt_data);
arma::vec Y = objfn_data-> Y ;
arma::mat X = objfn_data-> X ;
arma::vec mu = sigm (X*vals_inp);
const double norm_term = static_cast < double >(Y. n_elem );
const double obj_val = - arma::accu ( Y% arma::log (mu) + ( 1.0 -Y)% arma::log ( 1.0 -mu) ) / norm_term;
//
if (grad_out)
{
*grad_out = X. t () * (mu - Y) / norm_term;
}
//
if (hess_out)
{
arma::mat S = arma::diagmat ( mu%( 1.0 -mu) );
*hess_out = X. t () * S * X / norm_term;
}
//
return obj_val;
}
// log-likelihood function for Adam
double ll_fn ( const arma::vec& vals_inp, arma::vec* grad_out, void * opt_data)
{
return ll_fn_whess (vals_inp,grad_out, nullptr ,opt_data);
}
//
int main ()
{
int n_dim = 5 ; // dimension of parameter vector
int n_samp = 4000 ; // sample length
arma::mat X = arma::randn (n_samp,n_dim);
arma::vec theta_0 = 1.0 + 3.0 * arma::randu (n_dim, 1 );
arma::vec mu = sigm (X*theta_0);
arma::vec Y (n_samp);
for ( int i= 0 ; i < n_samp; i++)
{
Y (i) = ( arma::as_scalar ( arma::randu ( 1 )) < mu (i) ) ? 1.0 : 0.0 ;
}
// fn data and initial values
ll_data_t opt_data;
opt_data. Y = std::move (Y);
opt_data. X = std::move (X);
arma::vec x = arma::ones (n_dim, 1 ) + 1.0 ; // initial values
// run Adam-based optim
optim:: algo_settings_t settings;
settings. gd_method = 6 ;
settings. gd_settings . step_size = 0.1 ;
std::chrono::time_point<std::chrono::system_clock> start = std::chrono::system_clock::now ();
bool success = optim::gd (x,ll_fn,&opt_data,settings);
std::chrono::time_point<std::chrono::system_clock> end = std::chrono::system_clock::now ();
std::chrono::duration< double > elapsed_seconds = end-start;
//
if (success) {
std::cout << " Adam: logit_reg test completed successfully. n "
<< " elapsed time: " << elapsed_seconds. count () << " s n " ;
} else {
std::cout << " Adam: logit_reg test completed unsuccessfully. " << std::endl;
}
arma::cout << " n Adam: true values vs estimates: n " << arma::join_rows (theta_0,x) << arma::endl;
//
// run Newton-based optim
x = arma::ones (n_dim, 1 ) + 1.0 ; // initial values
start = std::chrono::system_clock::now ();
success = optim::newton (x,ll_fn_whess,&opt_data);
end = std::chrono::system_clock::now ();
elapsed_seconds = end-start;
//
if (success) {
std::cout << " newton: logit_reg test completed successfully. n "
<< " elapsed time: " << elapsed_seconds. count () << " s n " ;
} else {
std::cout << " newton: logit_reg test completed unsuccessfully. " << std::endl;
}
arma::cout << " n newton: true values vs estimates: n " << arma::join_rows (theta_0,x) << arma::endl;
return 0 ;
}Producción:
Adam: logit_reg test completed successfully.
elapsed time: 0.025128s
Adam: true values vs estimates:
2.7850 2.6993
3.6561 3.6798
2.3379 2.3860
2.3167 2.4313
2.2465 2.3064
newton: logit_reg test completed successfully.
elapsed time: 0.255909s
newton: true values vs estimates:
2.7850 2.6993
3.6561 3.6798
2.3379 2.3860
2.3167 2.4313
2.2465 2.3064
Al combinar a Eigen con la Biblioteca Autodiff, Optimlib proporciona soporte experimental para la diferenciación automática.
Ejemplo utilizando la diferenciación automática de modo avanzado con BFGS para la función de esfera:
# define OPTIM_ENABLE_EIGEN_WRAPPERS
# include " optim.hpp "
# include < autodiff/forward/real.hpp >
# include < autodiff/forward/real/eigen.hpp >
//
autodiff::real
opt_fnd ( const autodiff::ArrayXreal& x)
{
return x. cwiseProduct (x). sum ();
}
double
opt_fn ( const Eigen::VectorXd& x, Eigen::VectorXd* grad_out, void * opt_data)
{
autodiff::real u;
autodiff::ArrayXreal xd = x. eval ();
if (grad_out) {
Eigen::VectorXd grad_tmp = autodiff::gradient (opt_fnd, autodiff::wrt (xd), autodiff::at (xd), u);
*grad_out = grad_tmp;
} else {
u = opt_fnd (xd);
}
return u. val ();
}
int main ()
{
Eigen::VectorXd x ( 5 );
x << 1 , 2 , 3 , 4 , 5 ;
bool success = optim::bfgs (x, opt_fn, nullptr );
if (success) {
std::cout << " bfgs: forward-mode autodiff test completed successfully. n " << std::endl;
} else {
std::cout << " bfgs: forward-mode autodiff test completed unsuccessfully. n " << std::endl;
}
std::cout << " solution: x = n " << x << std::endl;
return 0 ;
}Compilar con:
g++ -Wall -std=c++17 -O3 -march=native -ffp-contract=fast -I/path/to/eigen -I/path/to/autodiff -I/path/to/optim/include optim_autodiff_ex.cpp -o optim_autodiff_ex.out -L/path/to/optim/lib -loptimVea la documentación para obtener más detalles sobre este tema.
Keith O'Hara
Apache versión 2