Ich war verwirrt über eine Veröffentlichung, die behauptete: Es ist möglich, Ihre FTP in einer Minute in Bikeradar zu messen . Weitere Googeln zeigten, dass Baronbiosys.com eine XERT-App entwickelte, die dies behauptet:
Die Methode verwendet ausgefeilte Techniken und Mustererkennung, um Ihre FTP zu bestimmen. Während Sie in der Vergangenheit beispielsweise entweder mit einem 20 -minütigen FTP -Protokoll testen oder viele Monate von Daten untersuchen müssen, um einen realistischen FTP -Wert zu erhalten, ermöglicht diese Methode, Ihre FTP an diesem Tag oder in diesem Moment zu bestimmen. CF Baronbiosys
Nachdem ich die XERT -App in meinem Garmin (830) installiert hatte, habe ich erlebt, bis die kostenlose Versuchszeit ausgegeben wurde, dass sie die Schätzungen von FTP bemerkenswert gut durchführen. DcrainMaker hat es überprüft und ist ziemlich positiv über seine Leistung und Genauigkeit und kam zu dem Schluss:
Hier ist es die Tatsache, dass ich in Echtzeit FTP-Feedback bekomme, das so einzigartig ist. Ich kann mitfahren und diese Werte formulieren sehen, während ich harte Anstrengungen bemühe. Keine Wartezeit oder sogar Minuten später. Mir ist keine andere Plattform oder App bekannt, die das tut. vgl. dcrainmaker
Ich habe mich entschlossen, C ++ - Code für eine Innen -Trainingsanwendung zu entwickeln, die auf einem Arduino NRF52840 Express -Board ausgeführt wird und der die Funktionalität der XERT -App (für Garmin Connect) so nah wie möglich kommt. Es wurde ein integraler Bestandteil eines größeren Projekts: Luftstrom. Das Folgende ist eine Erklärung der Wissenschaft und Mathematik hinter ihren Grundlagen.
Mir war klar, dass die XERT-App auf der Erschöpfung der sogenannten anaeroben Arbeitskapazität ( AWC ) oder der funktionalen Reservekapazität ( FRC ) basiert. Um es einfach zu halten, nehmen Sie an, dass ein Radfahrer eine bestimmte Menge davon hat Endliche Arbeitskapazität (eine Energiereserve) zu Beginn einer Fahrt intern aufbewahrt. Diese Energiemenge ist in mathematischen Begriffen als W ' (aussprechen W -Primem ) bekannt, sie ist Energie und wird folglich in Joule gemessen. Während Sie mit geringer Intensität fahren, bleibt W ' auf dem gesamten Niveau, da es nicht aufgewendet wird, und Sie können lange Zeit weiterhin in dieser Intensität fahren. Wenn Sie jedoch härter drücken, werden Sie diese Energie nutzen. Die Grenze, an der Sie diese Energiereserve verbrauchen, wird als Critical Power ( CP ) bezeichnet. Wenn Sie die Pedale härter als CP drücken, nimmt W ' ab. Sobald Ihre produzierte Leistung (Watt) niedriger wird als CP , wird W ' „regenerieren“, und die Energiereserve wird wieder zunehmen. Wenn Sie lange genug unter CP fahren, nähert sich W ' wieder dem 100% -Pegel. Wenn Sie jedoch hart und lange über CP arbeiten, wird W ' vollständig erschöpft und Sie werden im Moment erschöpft (auch bekannt als Lim )! Die Variationen in W ' werden im Dr. Skiba -Algorithmus (2) als „ W' Balance “ ausgedrückt. Ein weiterer Parameter des Algorithmus ist Tau , der die Geschwindigkeit definiert, mit der W ' regeneriert, wenn die Leistung unter CP liegt.
CP ist definiert als die höchste Trainingsintensität, die über längere Zeiträume gehalten werden kann, typischerweise 45 bis 60 Minuten. Die Funktionsschwellenleistung ( FTP ) ist im Freizeitradfahren besser bekannt und wurde als die höchste durchschnittliche Leistung definiert, die 60 Minuten lang beibehalten werden kann (1). Angesichts der großen Ähnlichkeit in der Definition gehen wir für Nicht-Eliten-Radfahren an, das Fehlen eines signifikanten Unterschieds zwischen CP- und FTP- Werten!
Die Algorithmen, die implementiert werden mussten, sind der ursprüngliche Dr. Skiba -Algorithmus (2) und eine Optimierung (Näherung) des integralen Skiba -Algorithmus von Dave Waterworth (3). Aart Goossens veröffentlichte Code (in Python) und erklärende Informationen zu Github (4), die sehr geholfen haben, die verschiedenen Algorithmen in einer Arduino -Umgebung zu verstehen und zu implementieren. Die folgenden Informationen werden aus seiner ursprünglichen Arbeit umgeschrieben, um dem Leser einen Einblick in den mathematischen Hintergrund der Algorithmen zu geben, siehe seine Arbeit bei: Aart Goosens @ github
Der integrale Skiba-Algorithmus ist der bekannteste Algorithmus zur Berechnung des W-Gleichgewichts und wurde wissenschaftlich validiert (5). Die Gleichungen für den Algorithmus sind: 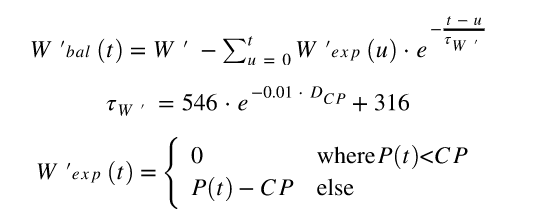
Wob Die Zahlen 546, -0,01 und 316 werden in Skibas ursprünglichem Artikel experimentell ermittelt und ändern sich nicht zwischen Individuen. D CP ist der Unterschied zwischen CP und der durchschnittlichen Leistung der Intervalle, in denen die Leistung unter CP lag. D CP kann dynamisch berechnet werden (der Durchschnitt bis zum Zeitpunkt t ) oder einmal für das gesamte Training berechnet und als statischer Wert verwendet werden. Skiba empfiehlt, einen statischen Wert für D CP zu verwenden . P (t) ist die zum Zeitpunkt t .
Der Mathematiker Dave Waterworth (3) half dem Kernentwickler von Golden Cheetah Mark Liversedge, eine Optimierung des Skiba -Algorithmus (6) zu entwickeln. Diese Reformulation nähert sich dem Skiba -Algorithmus, sodass die Ergebnisse in Extremfällen nur ein wenig variieren können, insbesondere wenn ( Tau ) im Vergleich zur Stichprobenzeit sehr gering ist. Der integrale Teil der W ' BAL -Teil der Gleichungen von Skiba wird von Waterworth umgeschrieben: 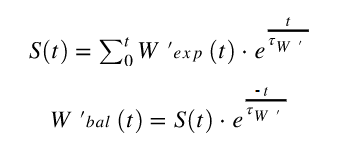
Wenn s (t) eine laufende Summe zum Zeitpunkt t nach dem Start ist, entsprechen andere Symbole den vorherigen Gleichungen. Tau (ʈ W ' ) und W' exp (t) werden mit den ursprünglichen Gleichungen von Skiba berechnet. Der integrale Skiba -Algorithmus ist selbst bei schnellen Computern ziemlich teuer, da die Summierung für jedes Mal wiederholt werden muss. Der große Vorteil der Waterworth -Optimierung besteht darin, dass w 'Gleichgewicht zu Echtzeit berechnet werden kann: während der Fahrt und nicht nur danach! Darüber hinaus ist es sehr hilfreich, wenn man die kritische Leistung während des HIIT -Trainings oder anstrengenden Trainings ermitteln möchte, wenn W 'Balance negativ wird und erschöpft wurde!
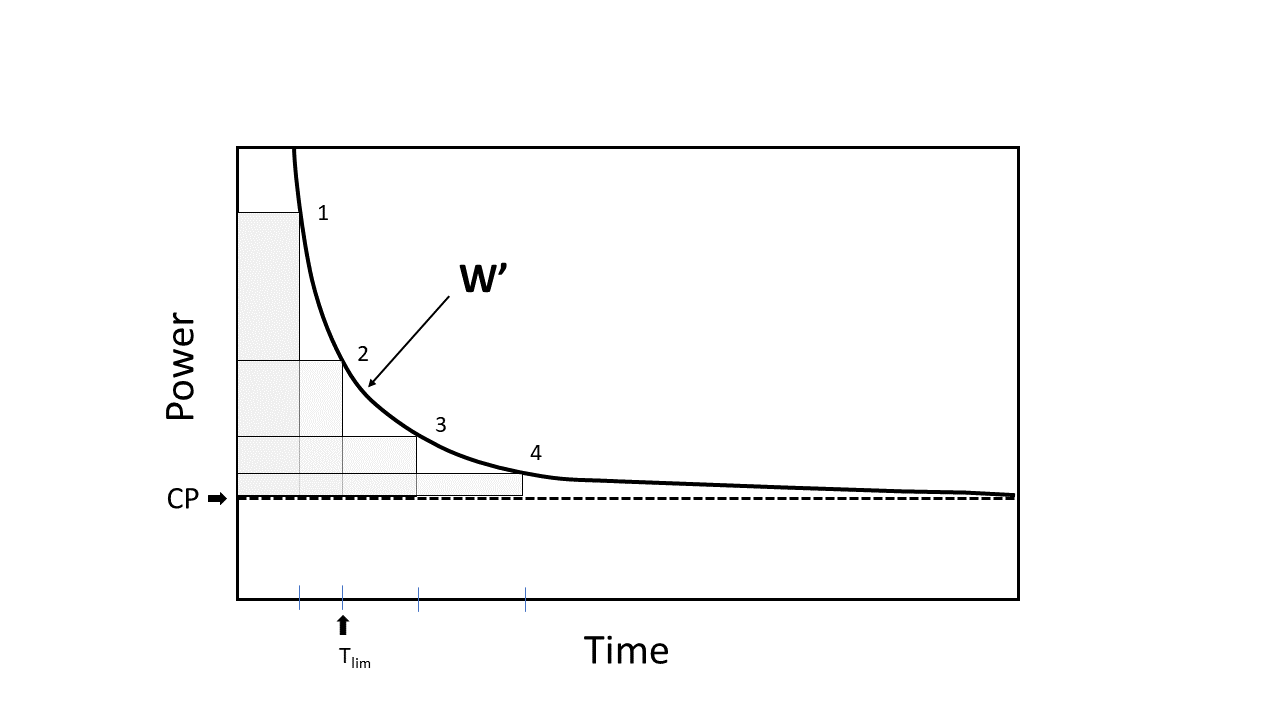
Mathematisch wird die Leistungsdauerbeziehung als hyperbolische Funktion beschrieben. Die 4 verschiedenen Punkte auf der Kurve repräsentieren Zeitpunkte ( T lim ), wenn die entsprechende maximale nachhaltige Leistung über dem CP erreicht wird und die Erschöpfung erfolgt. Bei Betrachtung der Übungstoleranz ist die Macht-Asymptote als CP (Watts) bekannt. Die Krümmungskonstante wird als w ' (dh W -Prime ) bekannt, sie wird in Einheiten der geleisteten Arbeiten (Joule) gemessen. Beachten Sie, dass die 4 grauten Gebiete, die W ' darstellen, in Form unterschiedlich sind, aber ungefähr gleich groß sind. Diese hyperbolische Beziehung zwischen Kraftdauer kann in eine lineare Beziehung umgewandelt werden, wenn die durchgeführte Arbeit gegen die Zeit aufgetragen wird, so dass die Steigung der Linie CP und der Abfang gleich w ' entspricht. Es sollte betont werden, dass die Macht-Dauer-Beziehung die Übungstoleranz beschreibt, sie jedoch nicht erklärt. Dennoch können die physiologischen Reaktionen auf Bewegung, die unter und über CP durchgeführt werden, wichtige Einblicke in den Ermüdungsprozess liefern. CP wurde ursprünglich als die externe Leistung definiert, die „auf unbestimmte Zeit“ oder für eine sehr lange Zeit ohne Müdigkeit aufrechterhalten werden konnte. Diese Definition sollte jedoch als theoretisch angesehen werden, da keine Übung auf unbestimmte Zeit durchgeführt werden kann. Es wird nun verstanden, dass CP Leistungsausgänge trennt, für die die Übungsverträglichkeit vorhersehbar begrenzt ist (Übungsleistung> CP ). Die tatsächliche Zeit für Intoleranz ( T LIM ) für das oben durchgeführte Training ist durch die Gleichung definiert und daher genau vorhergesagt:
T lim = w '/(P-CP)
In dieser Gleichung wird hervorgehoben, dass die Zeit für Intoleranz über CP eine Funktion der Nähe des Leistungsausgangs ( P ) auf CP und der Größe von W ' ist. Wenn P erheblich über CP liegt, wird die konstante Menge an Arbeiten, die durch den W' -Parameter dargestellt wird, schnell verwendet und T LIM ist kurz. Sollte P näher an CP sein, dann würde W ' langsamer "benutzt" und T lim länger sein. Eine entscheidende Überlegung hier ist, dass W ' für alle P. oben CP konstant ist. Dieses " zwei Parameter " -Prantzeit- oder Leistungsdauermodell impliziert daher, dass die absolute Übungsleistung einfach vom Wert von CP (in Watts) und dem Wert von W (in Joule) abhängt. Sowohl CP- als auch W' -Parameter können bei Personen in Abhängigkeit von Gesundheit/Krankheit, Alter, Fitness und Training erheblich variieren.
// ------------ W' Balance calculation -------------------
// Global variables related to Cycling Power and W-Prime
uint16_t TAWC_Mode = 1 ; // Track Anaerobic Capacity Depletion Mode == TRUE -> APPLY and SHOW
uint16_t CP60 = 160 ; // Your (estimate of) Critical Power, more or less the same as FTP
uint16_t eCP = CP60; // Algorithmic estimate of Critical Power during intense workout
uint16_t w_prime_usr = 7500 ; // Your (estimate of) W-prime or a base value
uint16_t ew_prime_mod = w_prime_usr; // First order estimate of W-prime modified during intense workout
uint16_t ew_prime_test = w_prime_usr; // 20-min-test algorithmic estimate (20 minute @ 5% above eCP) of W-prime for a given eCP!
long int w_prime_balance = 0 ; // Can be negative !!!
bool IsShowWprimeValuesDominant = false ; // Boolean that determines to show W Prime data on Oled or not
// ------------------------------------------------------- // ------------------------ W'Balance Functions -----------------------------------
uint16_t CalculateAveragePowerBelowCP ( uint16_t iPower, uint16_t iCP);
void CalculateAveragePowerAboveCP ( uint16_t iPower, uint16_t &iavPwr, unsigned long &iCpACp);
double tau_w_prime_balance ( uint16_t iPower, uint16_t iCP);
void w_prime_balance_waterworth ( uint16_t iPower, uint16_t iCP, uint16_t iw_prime);
void ConstrainW_PrimeValue ( uint16_t &iCP, uint16_t &iw_prime);
uint16_t GetCPfromTwoParameterAlgorithm ( uint16_t iav_Power, unsigned long iT_lim, uint16_t iw_prime);
uint16_t GetWPrimefromTwoParameterAlgorithm ( uint16_t iav_Power, double iT_lim, uint16_t iCP);
// ------------------------ W'Balance Functions ------------------------------------ uint16_t CalculateAveragePowerBelowCP ( uint16_t iPower, uint16_t iCP){
// calculate avg_power_below_cp real time using a running sum and counter
static unsigned long int CountPowerBelowCP = 0 ;
static unsigned long int SumPowerBelowCP = 0 ;
if (iPower < iCP) {
SumPowerBelowCP += ( unsigned long int )iPower;
CountPowerBelowCP++;
}
return uint16_t (SumPowerBelowCP/CountPowerBelowCP); // average power below CP
} // end calculate avg_power_below_cp
void CalculateAveragePowerAboveCP ( uint16_t iPower, uint16_t &iavPwr, unsigned long int &iCpACp){
// calculate avg_power_above_cp real time using a running sum and counter
// returning the values by C++ reference!
static unsigned long int SumPowerAboveCP = 0 ;
SumPowerAboveCP += ( unsigned long int )iPower;
iCpACp++;
iavPwr = uint16_t (SumPowerAboveCP/iCpACp); // average power above CP
} // end calculate avg_power_above_cp
double tau_w_prime_balance ( uint16_t iPower, uint16_t iCP){
uint16_t avg_power_below_cp = CalculateAveragePowerBelowCP (iPower, iCP);
double delta_cp = double (iCP - avg_power_below_cp);
return ( double ( 546.00 ) * exp (- 0.01 * delta_cp) + double ( 316.00 ));
} // end Tau W Prime Balance
void w_prime_balance_waterworth ( uint16_t iPower, uint16_t iCP, uint16_t iw_prime) {
// Most power meters measure power, torque a.o. in a high frequency (20-60 Hz) but
// transmit (BLE) datasets to a monitoring device in much lower frequency: 1-4 times per second.
int power_above_cp = 0 ; // Power > CP
static double T_lim = 0 ; // Time (duration) while Power is above CP, the summed value of every sample time value P > CP
double w_prime_expended = 0.0 ; // Expended energy in Joules
double ExpTerm1 = 0.0 , ExpTerm2 = 0.0 ;
static double TimeSpent = 0.0 ; // Total Time spent in the workout, the summed value of every sample time value
static double running_sum = 0.0 ;
static unsigned long int CountPowerAboveCP = 0 ; // Count the Power readings above CP
static uint16_t avPower = 0 ; // Average power above CP
const long int NextLevelStep = 1000 ; // Stepsize of the next level of w-prime modification --> 1000 Joules step
static long int NextUpdateLevel = 0 ; // The next level at which to update eCP, e_w_prime_mod and ew_prime_test
// Quarq Dfour Zero Spider power meter sends between 2 and 1.2 power readings per second, dependent of POWER level !!!
// We assume that the sample frequency (number of samples per second) is VARIABLE !!!
// Determine the individual sample time in seconds, it may/will vary during the workout !!!
static unsigned long PrevReadingTime = 0 ;
double SampleTime = double ( millis ()-PrevReadingTime)/ 1000 ; // Time or duration since the previous sample, convert from millis to seconds
PrevReadingTime = millis (); // Update for the next sample
double tau = tau_w_prime_balance (iPower, iCP); // Determine the value for tau
TimeSpent += SampleTime ; // The summed value of all sample time values during the workout
power_above_cp = (iPower - iCP);
# ifdef DEBUGAIR
Serial. printf ( " Time:%6.1f ST: %4.2f tau: %f " , TimeSpent, SampleTime , tau);
# endif
// w_prime is energy and measured in Joules = Watt*second
// Determine the expended energy above CP since the previous measurement (--> i.e. during sample time)
w_prime_expended = double ( max ( 0 , power_above_cp))*SampleTime; // Determine (Watts_above_CP) * (its duration in seconds) = expended energy in Joules!
// Calculate some terms of the equation
ExpTerm1 = exp (TimeSpent/tau); // Exponential term1
ExpTerm2 = exp (-TimeSpent/tau); // Exponential term2
# ifdef DEBUGAIR
Serial. printf ( " W prime expended: %3.0f exp-term1: %f exp-term2: %f " , w_prime_expended , ExpTerm1, ExpTerm2);
# endif
running_sum = running_sum + (w_prime_expended*ExpTerm1); // Determine the running sum
# ifdef DEBUGAIR
Serial. printf ( " Running Sum: %f " , running_sum);
# endif
w_prime_balance = ( long int )( ( double )iw_prime - (running_sum*ExpTerm2) ) ; // Determine w prime balance and cast from double to int
# ifdef DEBUGAIR
Serial. printf ( " w_prime_balance: %d " , w_prime_balance);
# endif
// --------------- extra --------------------------------------------------------------------------------------
// Workout starts at a certain W'= ##,### Joules and CP = ### watts, set by the user; the algorithm increases CP and W' stepwise
// to more realistic values every time when W'balance is depleted to a certain level; -> 2-Parameter Algorithm updates CP and W'
if (power_above_cp > 0 ) {
CalculateAveragePowerAboveCP (iPower, avPower, CountPowerAboveCP); // Average power above CP is to be calculated for future use
T_lim += SampleTime ; // Time to exhaustion: the accurate sum of every second spent above CP, calculated for future use
}
# ifdef DEBUGAIR
Serial. printf ( " [%d] n " , CountPowerAboveCP);
# endif
// When working above CP, the moment comes that we need to update eCP and ew_prime !!
if ( (w_prime_balance < NextUpdateLevel) && (w_prime_expended > 0 ) ) { // W' balance is further depleted --> test for an update moment
NextUpdateLevel -= NextLevelStep; // Move down another level of depletion, update eCP, ew_prime_mod and ew_prime_test
eCP = GetCPfromTwoParameterAlgorithm (avPower, T_lim, iw_prime); // Estimate a new eCP value
ew_prime_mod = w_prime_usr - NextUpdateLevel; // Adjust ew_prime_modified to the next level of depletion to be checked
ew_prime_test = GetWPrimefromTwoParameterAlgorithm ( uint16_t (eCP* 1.045 ), double ( 1200 ), eCP); // 20-Min-test estimate for W-Prime
# ifdef DEBUGAIR
Serial. printf ( " Update of eCP - ew_prime %5d - avPower: %3d - T-lim:%6.1f --> eCP: %3d " , ew_prime_mod, avPower, T_lim, eCP);
Serial. printf ( " --> Test estimate of W-Prime: %d n " , ew_prime_test );
# endif
}
// -----------------extra -------------------------------------------------------------------------------
} // end
// Check and Set starting value of w_prime to realistic numbers!!
void ConstrainW_PrimeValue ( uint16_t &iCP, uint16_t &iw_prime) {
if (iCP < 100 ) { iCP = 100 ; } // Update to lowest level that we allow for
// First determine the "minimal" value for W_Prime according to a 20-min-test estimate, given the iCP value!
uint16_t w_prime_estimate = GetWPrimefromTwoParameterAlgorithm ( uint16_t (iCP* 1.045 ), double ( 1200 ), iCP);
if (iw_prime < w_prime_estimate) { iw_prime = w_prime_estimate; } // Update iw_prime to a realistic level
return ;
} // end
uint16_t GetCPfromTwoParameterAlgorithm ( uint16_t iav_Power, double iT_lim, uint16_t iw_prime) {
uint16_t WprimeDivTlim = uint16_t ( double (iw_prime)/iT_lim ); // type cast for correct calculations
if (iav_Power > WprimeDivTlim){ // test for out of scope
return (iav_Power - WprimeDivTlim); // Solve 2-parameter algorithm to estimate CP
} else {
return eCP; // Something went wrong do'nt allow an update of CP
}
} // end
uint16_t GetWPrimefromTwoParameterAlgorithm ( uint16_t iav_Power, double iT_lim, uint16_t iCP) {
if (iav_Power > iCP){ // test for out of scope
return (iav_Power-iCP)*(( uint16_t )iT_lim); // Solve 2-parameter algorithm to estimate new W-Prime
} else {
return w_prime_usr; // Something went wrong don't allow an update of w_prime
}
} // end
Der Code wurde in ein größeres Projekt namens Airflow integriert. Das Einstellen oder Ändern Ihres Basal -CP und W Prime ist ein wesentlicher Bestandteil einer Airflow Companion -App! Das Luftstrom- Smart-Gerät stimmt kontinuierlich die angeforderte Luftstromgeschwindigkeit der Kühlventilatoren für ein stabiles Wärmeausgleich in allen Phasen eines Innentor-Radfahrens, Aufwärmen, Intensitätsintervalle, intermittierender Wiederherstellung und an der Abklingzeit ab. Der Radfahrer hat keine Störungen auf dem Weg und kann sich voll und ganz auf die Anforderungen des Trainingststabentrainers konzentrieren, der immer dem idealen Airstrom ausgesetzt ist, der ihn/sie angemessen abkühlt. Darüber hinaus erhalten die Radfahrer (als Bonus) Einblick in die Entwicklung seiner kritischen Kraft , wenn die Trainingsintensität intensiv und lang genug ist! Die angewendete ARDUINO NRF52480 Express CPU ist so mächtig, dass die Echtzeitberechnung von CP und W Prime alle Berechnungen zur Bestimmung der Wärmeausgleichsbegriffe und der Festlegung der Lüfter auf die entsprechende Blaskapazität durchführen kann.
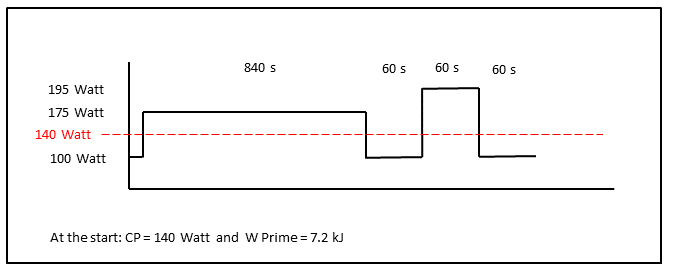
Ein Radfahrer (Eigenschaften: CP = 140 Watt und W Prime = 7,2 kJ ) macht ein intensives Training mit der Dauer und Intensität, wie in der Abbildung gezeigt. W Prime wird während des ersten Intervallblocks mehrmals erschöpft. Neue Werte für CP und W Prime werden vom Algorithmus während der Trainingszeit nur gegebenenfalls geschätzt. Führen Sie das Video aus, um eine 100% ige Depletion von W Prime und die geschätzten Werte zu sehen, wie sie in Echtzeit berechnet und auf einem OLED -Bildschirm präsentiert wurden ... Beachten Sie, wie die horizontale Balken bei der Stromversorgung von 175 und 195 Watt über CP liegt. Die Stange ist proportional mit W 'Gleichgewicht und außerdem wird das, was "im Tank übrig geblieben" ist, als Prozentsatz gezeigt! Die Messwerte werden in einer akquirierten Reihenfolge angezeigt und entsprechen nicht die angegebene Zeitdauer des Trainings!