Me sorprendió una publicación que afirmó: es posible medir su FTP en un minuto en Bikeradar. Google más reveló que Baronbiosys.com desarrolló una aplicación Xert que afirma esto:
El método utiliza técnicas sofisticadas y reconocimiento de patrones para determinar su FTP. Mientras que en el pasado necesitaba probar utilizando un protocolo FTP de 20 minutos, por ejemplo, o examinar datos de muchos meses para obtener un valor FTP realista, este método le permite determinar su FTP ese día o incluso en ese momento. CF baronbiosys
Después de instalar la aplicación Xert en mi Garmin (830), he experimentado, hasta que se haya gastado el tiempo de prueba gratuito, que hace sus estimaciones de FTP notablemente bien. Drainmaker lo revisó y es bastante positivo sobre su rendimiento y precisión y concluyó:
Mientras que aquí es el hecho de que recibo comentarios FTP en tiempo real que es tan único. Puedo salir a dar un paseo y comenzar a ver estos valores formulados ya que estoy dando esfuerzos difíciles. No hay horas de espera, o incluso minutos después. No conozco ninguna otra plataforma o aplicación que lo haga. cf dcrainmaker
Decidí desarrollar el código C ++ para una aplicación de capacitación en interiores que se ejecuta en una placa Arduino NRF52840 Express y que se acerca lo más posible a la funcionalidad de la aplicación Xert (para Garmin Connect). Se convirtió en una parte integral de un proyecto más grande: el flujo de aire. La siguiente es una explicación de la ciencia y las matemáticas detrás de sus fundamentos.
Para mí estaba claro que la aplicación Xert se basa en el agotamiento de la llamada capacidad de trabajo anaerobia ( AWC ) o la capacidad de reserva funcional ( FRC ). Para mantenerlo simple, suponga que un ciclista tiene una cantidad determinada de esto capacidad de trabajo finito (una reserva de energía) almacenada internamente al comienzo de un viaje. Esta cantidad de energía se conoce en términos matemáticos como w ' (pronunciado w prime ), es energía y, en consecuencia, se mide en julios. Mientras viaja a baja intensidad, W ' permanece en su nivel completo ya que no se gasta, y puede continuar montando a esta intensidad durante mucho tiempo. Pero si presiona más fuerte, comenzará a usar esta energía. El límite al que comenzará a gastar esta reserva de energía se conoce como potencia crítica ( CP ). Si empuja los pedales más duro que CP , W ' disminuirá. Tan pronto como su potencia producida (vatios) se vuelva más baja que la CP , W ' se "regenerará", y la reserva de energía aumentará nuevamente. Cuando viaja lo suficiente por debajo de CP , W ' se acercará al nivel del 100% nuevamente. Sin embargo, cuando trabaje duro y lo suficientemente largo por encima de CP , W ' se agotará por completo y estará agotado en el mismo momento (también conocido como T Lim ). Las variaciones en w ' se expresan como " balance w' " en el algoritmo del Dr. Skiba (2). Otro parámetro del algoritmo es tau que define la velocidad a la que W ' se está regenerando cuando la potencia está por debajo de CP .
CP se define como la intensidad del ejercicio más alta que se puede mantener durante períodos prolongados de tiempo, generalmente durante 45 a 60 min. La potencia del umbral funcional ( FTP ) es más conocida en el ciclo recreativo y se ha definido como la potencia de salida promedio más alta que se puede mantener durante 60 minutos (1). ¡Dada la gran similitud en la definición, suponemos que para el ciclismo no de élite la ausencia de una diferencia significativa entre los valores de CP y FTP !
Los algoritmos que tuvieron que implementarse son el algoritmo original del Dr. Skiba (2) y una optimización (aproximación) del algoritmo integral de Skiba por Dave Waterworth (3). AART GOOSSENS Código publicado (en Python) e información explicativa sobre GitHub (4) que ayudó mucho a comprender e implementar los diferentes algoritmos en un entorno Arduino. La siguiente información se parafrasea de su trabajo original, para darle al lector una idea de los antecedentes matemáticos de los algoritmos, vea su trabajo en: aart Goosens @ github
El algoritmo SKIBA integral es el algoritmo más conocido para calcular el equilibrio W ' y ha sido validado científicamente (5). Las ecuaciones para el algoritmo son: 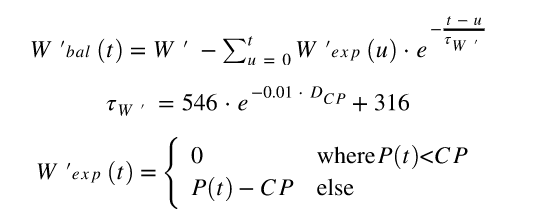
Donde w ' bal (t) es igual a w' bal en el tiempo t , w ' es la cantidad de energía disponible por encima de CP (potencia crítica), el tiempo para el que se calcula w' BAL , U el iterador de la suma, w ' exp (u) cantidad de energía por encima de CP que se usa en el tiempo u (se gasta) el número deuler y ʈ w' (pronunciado tau ) un tiempo constante que describe la velocidad de recuperación. Los números 546, -0.01 y 316 se determinan experimentalmente en el artículo original de Skiba y no cambian entre individuos. D CP es la diferencia entre CP y la potencia promedio de los intervalos en los que la potencia estaba por debajo de CP . D CP se puede calcular dinámicamente (el promedio hasta el tiempo t ) o calcularse una vez para todo el entrenamiento y usarse como un valor estático. Skiba recomienda usar un valor estático para D CP . P (t) es el poder producido en el tiempo t .
El matemático Dave Waterworth (3) ayudó al desarrollador central de Golden Cheetah, Mark Liversedge, a desarrollar una optimización del algoritmo Skiba (6). Esta reformulación se aproxima al algoritmo Skiba, por lo que los resultados pueden variar un poco solo en casos extremos, especialmente cuando ( tau ) es muy pequeño en comparación con el tiempo de muestra. La parte integral de W ' Bal de las ecuaciones de Skiba es reescrita por Waterworth a: 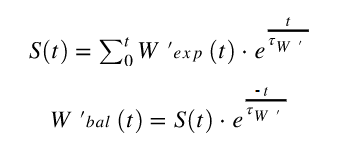
Donde s (t) es una suma en ejecución en el tiempo t Después del inicio, otros símbolos conforman las ecuaciones anteriores. Tau (ʈ w ' ) y w' exp (t) se calculan con las ecuaciones originales presentadas por Skiba. El algoritmo integral de Skiba es bastante costoso de calcular, incluso en computadoras rápidas, ya que la suma debe repetirse cada vez que T nuevamente. La gran ventaja de la optimización de Waterworth es que ahora se puede calcular el equilibrio W ' en tiempo real: ¡durante el viaje y no solo después! Además, es muy útil cuando uno quiere determinar el poder crítico de la marcha durante los entrenamientos HIIT o los entrenamientos extenuantes cuando el equilibrio W ' se vuelve negativo y se ha agotado.
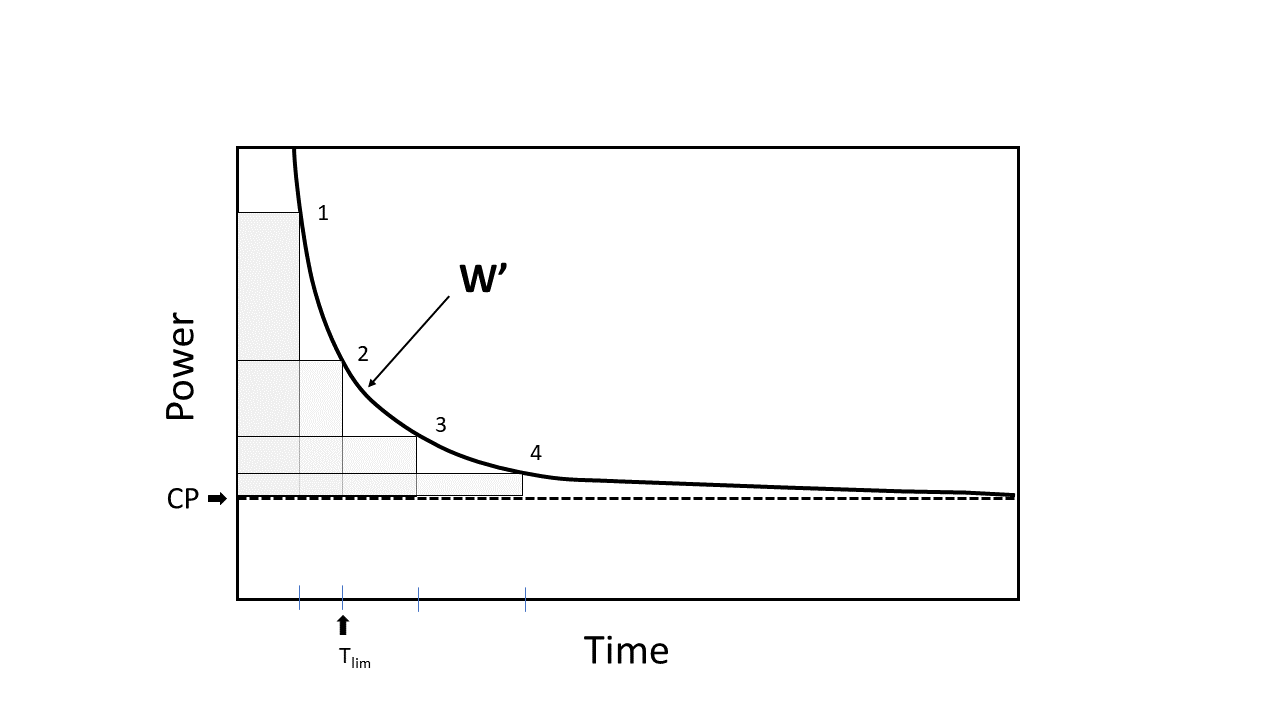
Matemáticamente, la relación de duración de la potencia se describe como una función hiperbólica. Los 4 puntos diferentes en la curva representan puntos en el tiempo ( T lim ) cuando se alcanza la potencia máxima sostenible correspondiente por encima de CP y se produce agotamiento. Cuando se considera la tolerancia al ejercicio, la auxiliar de poder se conoce como CP (Watts). La constante de curvatura se conoce como w ' (es decir, w prime ), se mide en unidades de trabajo realizadas (julios). Observe que las 4 áreas grises, que representan W ' , son diferentes en forma pero son de igual tamaño. Esta relación hiperbólica de duración de potencia puede transformarse en una relación lineal si el trabajo realizado se traza contra el tiempo, de modo que la pendiente de la línea es igual a CP y la intersección es igual a w ' . Debe enfatizarse que la relación de duración de la potencia describe la tolerancia al ejercicio, pero no lo explica. Sin embargo, las respuestas fisiológicas al ejercicio realizadas por debajo y por encima de CP pueden proporcionar información importante sobre el proceso de fatiga. CP se definió originalmente como la potencia de salida externa que podría sostenerse "indefinidamente" o durante mucho tiempo sin fatiga. Sin embargo, esta definición debe considerarse teórica, ya que ningún ejercicio puede realizarse indefinidamente. Ahora se entiende que CP separa las salidas de energía para las cuales la tolerancia al ejercicio es previsiblemente limitada (potencia de ejercicio> CP ). El tiempo real de intolerancia ( T lim ) para el ejercicio realizado anteriormente CP se define y, por lo tanto, se predice estrechamente, por la ecuación:
T lim = w ′/(P-CP)
Esta ecuación destaca que el tiempo de intolerancia por encima de CP es una función de la proximidad de la potencia de salida ( P ) que se mantiene a CP y el tamaño de W ' . Cuando P está considerablemente por encima de CP , la cantidad constante de trabajo representada por el parámetro W ' se utilizará rápidamente y T lim será corta. Si P estará más cerca de CP , entonces w ' se' usaría 'más lentamente y T lim sería más largo. Una consideración crucial aquí es que se supone que W ' es constante para todas las P por encima de CP . Por lo tanto, este modelo de potencia o modelo de potencia de ' dos parámetros implica que el rendimiento absoluto del ejercicio depende simplemente del valor de CP (en vatios) y el valor de w' (en julios). Tanto los parámetros de CP como W ' pueden variar considerablemente entre las personas en función de la salud/enfermedad, la edad, el estado físico y el entrenamiento.
// ------------ W' Balance calculation -------------------
// Global variables related to Cycling Power and W-Prime
uint16_t TAWC_Mode = 1 ; // Track Anaerobic Capacity Depletion Mode == TRUE -> APPLY and SHOW
uint16_t CP60 = 160 ; // Your (estimate of) Critical Power, more or less the same as FTP
uint16_t eCP = CP60; // Algorithmic estimate of Critical Power during intense workout
uint16_t w_prime_usr = 7500 ; // Your (estimate of) W-prime or a base value
uint16_t ew_prime_mod = w_prime_usr; // First order estimate of W-prime modified during intense workout
uint16_t ew_prime_test = w_prime_usr; // 20-min-test algorithmic estimate (20 minute @ 5% above eCP) of W-prime for a given eCP!
long int w_prime_balance = 0 ; // Can be negative !!!
bool IsShowWprimeValuesDominant = false ; // Boolean that determines to show W Prime data on Oled or not
// ------------------------------------------------------- // ------------------------ W'Balance Functions -----------------------------------
uint16_t CalculateAveragePowerBelowCP ( uint16_t iPower, uint16_t iCP);
void CalculateAveragePowerAboveCP ( uint16_t iPower, uint16_t &iavPwr, unsigned long &iCpACp);
double tau_w_prime_balance ( uint16_t iPower, uint16_t iCP);
void w_prime_balance_waterworth ( uint16_t iPower, uint16_t iCP, uint16_t iw_prime);
void ConstrainW_PrimeValue ( uint16_t &iCP, uint16_t &iw_prime);
uint16_t GetCPfromTwoParameterAlgorithm ( uint16_t iav_Power, unsigned long iT_lim, uint16_t iw_prime);
uint16_t GetWPrimefromTwoParameterAlgorithm ( uint16_t iav_Power, double iT_lim, uint16_t iCP);
// ------------------------ W'Balance Functions ------------------------------------ uint16_t CalculateAveragePowerBelowCP ( uint16_t iPower, uint16_t iCP){
// calculate avg_power_below_cp real time using a running sum and counter
static unsigned long int CountPowerBelowCP = 0 ;
static unsigned long int SumPowerBelowCP = 0 ;
if (iPower < iCP) {
SumPowerBelowCP += ( unsigned long int )iPower;
CountPowerBelowCP++;
}
return uint16_t (SumPowerBelowCP/CountPowerBelowCP); // average power below CP
} // end calculate avg_power_below_cp
void CalculateAveragePowerAboveCP ( uint16_t iPower, uint16_t &iavPwr, unsigned long int &iCpACp){
// calculate avg_power_above_cp real time using a running sum and counter
// returning the values by C++ reference!
static unsigned long int SumPowerAboveCP = 0 ;
SumPowerAboveCP += ( unsigned long int )iPower;
iCpACp++;
iavPwr = uint16_t (SumPowerAboveCP/iCpACp); // average power above CP
} // end calculate avg_power_above_cp
double tau_w_prime_balance ( uint16_t iPower, uint16_t iCP){
uint16_t avg_power_below_cp = CalculateAveragePowerBelowCP (iPower, iCP);
double delta_cp = double (iCP - avg_power_below_cp);
return ( double ( 546.00 ) * exp (- 0.01 * delta_cp) + double ( 316.00 ));
} // end Tau W Prime Balance
void w_prime_balance_waterworth ( uint16_t iPower, uint16_t iCP, uint16_t iw_prime) {
// Most power meters measure power, torque a.o. in a high frequency (20-60 Hz) but
// transmit (BLE) datasets to a monitoring device in much lower frequency: 1-4 times per second.
int power_above_cp = 0 ; // Power > CP
static double T_lim = 0 ; // Time (duration) while Power is above CP, the summed value of every sample time value P > CP
double w_prime_expended = 0.0 ; // Expended energy in Joules
double ExpTerm1 = 0.0 , ExpTerm2 = 0.0 ;
static double TimeSpent = 0.0 ; // Total Time spent in the workout, the summed value of every sample time value
static double running_sum = 0.0 ;
static unsigned long int CountPowerAboveCP = 0 ; // Count the Power readings above CP
static uint16_t avPower = 0 ; // Average power above CP
const long int NextLevelStep = 1000 ; // Stepsize of the next level of w-prime modification --> 1000 Joules step
static long int NextUpdateLevel = 0 ; // The next level at which to update eCP, e_w_prime_mod and ew_prime_test
// Quarq Dfour Zero Spider power meter sends between 2 and 1.2 power readings per second, dependent of POWER level !!!
// We assume that the sample frequency (number of samples per second) is VARIABLE !!!
// Determine the individual sample time in seconds, it may/will vary during the workout !!!
static unsigned long PrevReadingTime = 0 ;
double SampleTime = double ( millis ()-PrevReadingTime)/ 1000 ; // Time or duration since the previous sample, convert from millis to seconds
PrevReadingTime = millis (); // Update for the next sample
double tau = tau_w_prime_balance (iPower, iCP); // Determine the value for tau
TimeSpent += SampleTime ; // The summed value of all sample time values during the workout
power_above_cp = (iPower - iCP);
# ifdef DEBUGAIR
Serial. printf ( " Time:%6.1f ST: %4.2f tau: %f " , TimeSpent, SampleTime , tau);
# endif
// w_prime is energy and measured in Joules = Watt*second
// Determine the expended energy above CP since the previous measurement (--> i.e. during sample time)
w_prime_expended = double ( max ( 0 , power_above_cp))*SampleTime; // Determine (Watts_above_CP) * (its duration in seconds) = expended energy in Joules!
// Calculate some terms of the equation
ExpTerm1 = exp (TimeSpent/tau); // Exponential term1
ExpTerm2 = exp (-TimeSpent/tau); // Exponential term2
# ifdef DEBUGAIR
Serial. printf ( " W prime expended: %3.0f exp-term1: %f exp-term2: %f " , w_prime_expended , ExpTerm1, ExpTerm2);
# endif
running_sum = running_sum + (w_prime_expended*ExpTerm1); // Determine the running sum
# ifdef DEBUGAIR
Serial. printf ( " Running Sum: %f " , running_sum);
# endif
w_prime_balance = ( long int )( ( double )iw_prime - (running_sum*ExpTerm2) ) ; // Determine w prime balance and cast from double to int
# ifdef DEBUGAIR
Serial. printf ( " w_prime_balance: %d " , w_prime_balance);
# endif
// --------------- extra --------------------------------------------------------------------------------------
// Workout starts at a certain W'= ##,### Joules and CP = ### watts, set by the user; the algorithm increases CP and W' stepwise
// to more realistic values every time when W'balance is depleted to a certain level; -> 2-Parameter Algorithm updates CP and W'
if (power_above_cp > 0 ) {
CalculateAveragePowerAboveCP (iPower, avPower, CountPowerAboveCP); // Average power above CP is to be calculated for future use
T_lim += SampleTime ; // Time to exhaustion: the accurate sum of every second spent above CP, calculated for future use
}
# ifdef DEBUGAIR
Serial. printf ( " [%d] n " , CountPowerAboveCP);
# endif
// When working above CP, the moment comes that we need to update eCP and ew_prime !!
if ( (w_prime_balance < NextUpdateLevel) && (w_prime_expended > 0 ) ) { // W' balance is further depleted --> test for an update moment
NextUpdateLevel -= NextLevelStep; // Move down another level of depletion, update eCP, ew_prime_mod and ew_prime_test
eCP = GetCPfromTwoParameterAlgorithm (avPower, T_lim, iw_prime); // Estimate a new eCP value
ew_prime_mod = w_prime_usr - NextUpdateLevel; // Adjust ew_prime_modified to the next level of depletion to be checked
ew_prime_test = GetWPrimefromTwoParameterAlgorithm ( uint16_t (eCP* 1.045 ), double ( 1200 ), eCP); // 20-Min-test estimate for W-Prime
# ifdef DEBUGAIR
Serial. printf ( " Update of eCP - ew_prime %5d - avPower: %3d - T-lim:%6.1f --> eCP: %3d " , ew_prime_mod, avPower, T_lim, eCP);
Serial. printf ( " --> Test estimate of W-Prime: %d n " , ew_prime_test );
# endif
}
// -----------------extra -------------------------------------------------------------------------------
} // end
// Check and Set starting value of w_prime to realistic numbers!!
void ConstrainW_PrimeValue ( uint16_t &iCP, uint16_t &iw_prime) {
if (iCP < 100 ) { iCP = 100 ; } // Update to lowest level that we allow for
// First determine the "minimal" value for W_Prime according to a 20-min-test estimate, given the iCP value!
uint16_t w_prime_estimate = GetWPrimefromTwoParameterAlgorithm ( uint16_t (iCP* 1.045 ), double ( 1200 ), iCP);
if (iw_prime < w_prime_estimate) { iw_prime = w_prime_estimate; } // Update iw_prime to a realistic level
return ;
} // end
uint16_t GetCPfromTwoParameterAlgorithm ( uint16_t iav_Power, double iT_lim, uint16_t iw_prime) {
uint16_t WprimeDivTlim = uint16_t ( double (iw_prime)/iT_lim ); // type cast for correct calculations
if (iav_Power > WprimeDivTlim){ // test for out of scope
return (iav_Power - WprimeDivTlim); // Solve 2-parameter algorithm to estimate CP
} else {
return eCP; // Something went wrong do'nt allow an update of CP
}
} // end
uint16_t GetWPrimefromTwoParameterAlgorithm ( uint16_t iav_Power, double iT_lim, uint16_t iCP) {
if (iav_Power > iCP){ // test for out of scope
return (iav_Power-iCP)*(( uint16_t )iT_lim); // Solve 2-parameter algorithm to estimate new W-Prime
} else {
return w_prime_usr; // Something went wrong don't allow an update of w_prime
}
} // end
El código se ha integrado en un proyecto más grande llamado Airflow . ¡Establecer o cambiar su CP Basal y W Prime son una parte integral de una aplicación complementaria de flujo de aire ! El dispositivo inteligente de flujo de aire sintoniza continuamente la velocidad del flujo de aire solicitado de los ventiladores de enfriamiento para un equilibrio de calor estable durante todas las fases de un entrenamiento de ciclismo interior, calentamiento, intervalos de intensidad, recuperación intermitente y enonelato. El ciclista no tiene interferencia en camino y puede concentrarse completamente en las demandas del entrenamiento del entrenador Stationay, siempre enfrentando el aire de aire ideal que lo enfriará adecuadamente. ¡Además, los ciclistas obtienen (como una bonificación) información en el desarrollo de su poder crítico cuando la intensidad de entrenamiento es intensa y lo suficientemente larga! La CPU express Express Apliced Arduino NRF52480 es tan poderosa que el cálculo en tiempo real de CP y W Prime se puede dejar de lado todos los cálculos para determinar los términos del equilibrio de calor y establecer los ventiladores en la capacidad de soplado apropiada.
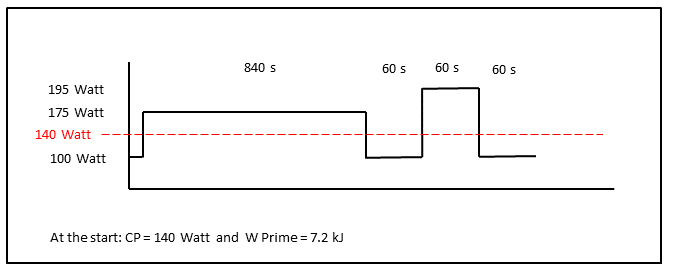
Un ciclista (Propiedades: CP = 140 vatios y W Prime = 7.2 kJ ) está haciendo un entrenamiento intenso con la duración y la intensidad como se muestra en la figura. W Prime se agota varias veces durante el primer bloque de intervalo. El algoritmo estimará los nuevos valores para CP y W Prime durante el tiempo de entrenamiento solo cuando sea apropiado. Ejecute el video para ver el 100% de agotamiento de W Prime y los valores estimados a medida que se calcularon en tiempo real y se presentaron en una pantalla OLED ... observe cómo la barra horizontal se encoge cuando la potencia está por encima de CP a 175 y 195 vatios. ¡La barra es proporcional con W 'Balance y, además, lo que está "dejando en el tanque" se muestra como un porcentaje! ¡Las lecturas se muestran en una secuencia acelerada y no conforman la duración del tiempo indicada del entrenamiento!