我對一份聲稱的出版物感到困惑:可以在Bikeradar的一分鐘內測量您的FTP 。進一步的谷歌搜索顯示,Baronbiosys.com開發了一個Xert-App ,聲稱這一點:
該方法使用複雜的技術和模式識別來確定您的FTP。過去,您要么需要使用20分鐘的FTP協議進行測試,要么檢查數月的數據以獲取現實的FTP值,因此此方法使您可以在當天甚至當時確定您的FTP。 CF男爵
在我的Garmin(830)上安裝Xert應用程序後,我已經經歷過,直到花費免費試用時間為止,它的估計值非常好。 Dcrainmaker對其進行了審查,並對其性能和準確性非常有肯定,並得出結論:
而這是我實時獲得FTP反饋的事實是如此獨特。我可以出去兜風,開始看到這些價值觀,因為我正在努力努力。沒有等待幾個小時,甚至幾分鐘後。我不知道這樣做的任何其他平台或應用程序。 CF DCRAINMAKER
我決定為室內培訓應用程序開發C ++代碼,該應用程序正在Arduino NRF52840 Express板上運行,並且與XERT應用程序的功能(對於Garmin Connect)盡可能近。它成為較大項目的組成部分:氣流。以下是對其基本面背後的科學和數學的解釋。
對我來說, XERT應用程序很明顯是基於所謂的厭氧工作能力( AWC )或功能儲備能力( FRC )的耗盡。為了保持簡單,假設騎自行車的人有一個給定的數量有限的工作能力(一個能源儲備)在乘車開始時內部存儲。這種能量在數學術語中被稱為w' (發音w prime ),它是能量,因此在焦耳中進行了測量。當您以低強度騎行時, W'由於沒有花費而保持完整水平,並且您可以長時間以這種強度繼續騎行。但是,如果您更加努力,您將開始使用這種能量。您開始使用此能源儲備的極限稱為關鍵功率( CP )。如果您比CP更難推動踏板,則W'將減少。一旦您產生的功率(瓦特)低於CP , W'將“再生”,能源儲備將再次增加。當您在CP以下騎行足夠長的時間時, W'將再次接近100%的水平。但是,當您努力工作且在CP上方足夠長的時間時, W'將完全耗盡,您將在那一刻筋疲力盡(又稱lim )! W'的變化表示為Skiba算法(2)中的“ w'平衡”。該算法的另一個參數是tau ,該參數定義了當功率低於CP時, W'重新生成的速度。
CP被定義為可以長時間維持的最高運動強度,通常為45至60分鐘。功能性閾值功率( FTP )在休閒循環中更為知名,已被定義為可以維持60分鐘(1)的最高平均功率輸出。鑑於定義上的相似性很大,我們假設非精英循環是CP和FTP值之間沒有顯著差異的情況!
必須實現的算法是Dave Waterworth(3)的原始Skiba算法(2)和整體Skiba算法的優化(近似)。 AART GOOSSENS發布了(在Python中)和有關Github(4)的解釋信息,這些信息有助於在Arduino環境中理解和實施不同的算法。以下信息從他的原始作品中得到了解釋,以在算法的數學背景中給讀者一些見解,請參閱他的作品:aart goosens @ github
積分SKIBA算法是計算平衡並經過科學驗證的最著名的算法(5)。算法的方程是: 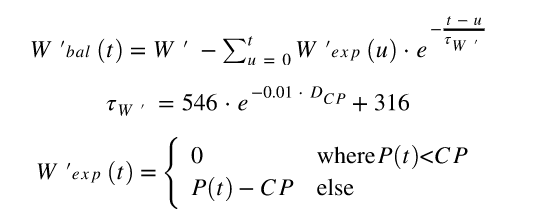
Where W' bal(t) is equal to W' bal at time t , W' is the amount of available energy above CP (Critical Power), t the time for which W' bal is calculated, u the iterator of the summation, W' exp(u) amount of energy above CP that is used at time u (expended), e the Euler number and Ʈ W' (pronounced Tau ) a time constant that describes the recovery speed.數字546,-0.01和316在Skiba的原始文章中實驗確定,並且在個人之間不會改變。 D CP是CP和功率低於CP的間隔的平均功率之間的差異。 D CP可以動態計算(直到時間t的平均值),也可以在整個鍛煉中計算一次,並用作靜態值。 Skiba建議使用D CP使用靜態值。 p(t)是時間t產生的功率。
數學家Dave Waterworth(3)幫助Mark Liversedge的Golden Cheetah的核心開發商開發了SKIBA算法的優化(6)。該重新印象近似於SKIBA算法,因此僅在極端情況下可能會有所不同,尤其是當( Tau )與樣品時間非常小時。沃特沃思( Waterworth 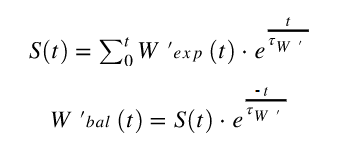
其中s(t)是啟動後時間t的運行總和,其他符號符合先前的方程式。 tau ( ʈw' )和w'exp (t)是用Skiba提出的原始方程計算的。即使在快速計算機上,整數SKIBA算法的計算也非常昂貴,因為必須再次重複求和。 Waterworth優化的最大優勢是,現在可以實時計算餘額:在騎行期間,不僅是之後!此外,當人們想在HIIT鍛煉過程中飛行或艱苦的鍛煉時,當w'平衡變得負面並耗盡時,這將非常有幫助!
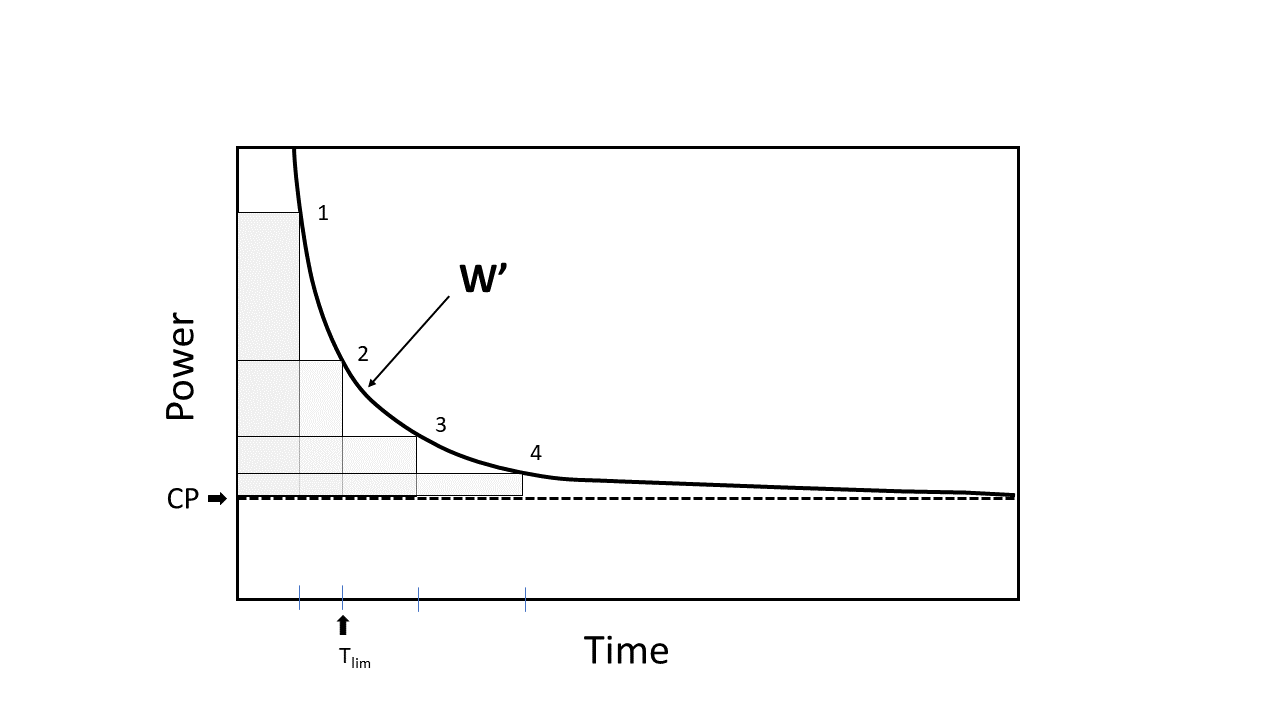
從數學上講,功率 - 持續關係被描述為雙曲線函數。當達到相應的最大可持續功率並發生疲憊時,曲線上的4個不同點表示時間點( T LIM )。當考慮運動耐受性時,功率拼合被稱為CP (瓦特)。曲率常數稱為w' (即, w prime ),以完成的工作單位(焦耳)進行測量。請注意,代表W'的4個灰色區域的形式不同,但大小相等。如果將完成的工作繪製在時間上,則可以將這種雙曲功率 - 持續關係變為線性關係,以使線的斜率等於CP和截距等於W' 。應該強調的是,力量持續關係描述了運動的寬容,但沒有解釋。然而,在CP下和更高的鍛煉中對運動的生理反應可能會為疲勞過程提供重要的見解。 CP最初被定義為可以“無限期”或很長時間內無疲勞的外部功率輸出。但是,該定義應被視為理論上,因為永遠無法無限期進行任何鍛煉。現在可以理解, CP可以將鍛煉公差的功率輸出分開,而鍛煉公差是可以預見的(運動功率> CP )。在上述CP上進行的鍛煉的實際不寬容時間( T LIM )是通過方程式定義的,因此可以仔細地預測:
t lim = w'/(p-cp)
該方程強調,不耐受性在CP上方的時間是功率輸出( P )持續到CP和W'的大小的鄰近的函數。當P高於CP時,將迅速使用由W'參數代表的恆定工作量,而T LIM將很短。如果P更靠近CP ,那麼W'將被更慢地“使用”,而T LIM將更長。這裡的關鍵考慮是,對於CP上方的所有P,都認為W'是恆定的。因此,這個“兩個參數”的功率時間或功率持續模型意味著絕對練習性能僅取決於CP的值(瓦特)和W'的值(在Joules中)。 CP和W'參數在個體中都可以差異,這是健康/疾病,年齡,健身和培訓的函數。
// ------------ W' Balance calculation -------------------
// Global variables related to Cycling Power and W-Prime
uint16_t TAWC_Mode = 1 ; // Track Anaerobic Capacity Depletion Mode == TRUE -> APPLY and SHOW
uint16_t CP60 = 160 ; // Your (estimate of) Critical Power, more or less the same as FTP
uint16_t eCP = CP60; // Algorithmic estimate of Critical Power during intense workout
uint16_t w_prime_usr = 7500 ; // Your (estimate of) W-prime or a base value
uint16_t ew_prime_mod = w_prime_usr; // First order estimate of W-prime modified during intense workout
uint16_t ew_prime_test = w_prime_usr; // 20-min-test algorithmic estimate (20 minute @ 5% above eCP) of W-prime for a given eCP!
long int w_prime_balance = 0 ; // Can be negative !!!
bool IsShowWprimeValuesDominant = false ; // Boolean that determines to show W Prime data on Oled or not
// ------------------------------------------------------- // ------------------------ W'Balance Functions -----------------------------------
uint16_t CalculateAveragePowerBelowCP ( uint16_t iPower, uint16_t iCP);
void CalculateAveragePowerAboveCP ( uint16_t iPower, uint16_t &iavPwr, unsigned long &iCpACp);
double tau_w_prime_balance ( uint16_t iPower, uint16_t iCP);
void w_prime_balance_waterworth ( uint16_t iPower, uint16_t iCP, uint16_t iw_prime);
void ConstrainW_PrimeValue ( uint16_t &iCP, uint16_t &iw_prime);
uint16_t GetCPfromTwoParameterAlgorithm ( uint16_t iav_Power, unsigned long iT_lim, uint16_t iw_prime);
uint16_t GetWPrimefromTwoParameterAlgorithm ( uint16_t iav_Power, double iT_lim, uint16_t iCP);
// ------------------------ W'Balance Functions ------------------------------------ uint16_t CalculateAveragePowerBelowCP ( uint16_t iPower, uint16_t iCP){
// calculate avg_power_below_cp real time using a running sum and counter
static unsigned long int CountPowerBelowCP = 0 ;
static unsigned long int SumPowerBelowCP = 0 ;
if (iPower < iCP) {
SumPowerBelowCP += ( unsigned long int )iPower;
CountPowerBelowCP++;
}
return uint16_t (SumPowerBelowCP/CountPowerBelowCP); // average power below CP
} // end calculate avg_power_below_cp
void CalculateAveragePowerAboveCP ( uint16_t iPower, uint16_t &iavPwr, unsigned long int &iCpACp){
// calculate avg_power_above_cp real time using a running sum and counter
// returning the values by C++ reference!
static unsigned long int SumPowerAboveCP = 0 ;
SumPowerAboveCP += ( unsigned long int )iPower;
iCpACp++;
iavPwr = uint16_t (SumPowerAboveCP/iCpACp); // average power above CP
} // end calculate avg_power_above_cp
double tau_w_prime_balance ( uint16_t iPower, uint16_t iCP){
uint16_t avg_power_below_cp = CalculateAveragePowerBelowCP (iPower, iCP);
double delta_cp = double (iCP - avg_power_below_cp);
return ( double ( 546.00 ) * exp (- 0.01 * delta_cp) + double ( 316.00 ));
} // end Tau W Prime Balance
void w_prime_balance_waterworth ( uint16_t iPower, uint16_t iCP, uint16_t iw_prime) {
// Most power meters measure power, torque a.o. in a high frequency (20-60 Hz) but
// transmit (BLE) datasets to a monitoring device in much lower frequency: 1-4 times per second.
int power_above_cp = 0 ; // Power > CP
static double T_lim = 0 ; // Time (duration) while Power is above CP, the summed value of every sample time value P > CP
double w_prime_expended = 0.0 ; // Expended energy in Joules
double ExpTerm1 = 0.0 , ExpTerm2 = 0.0 ;
static double TimeSpent = 0.0 ; // Total Time spent in the workout, the summed value of every sample time value
static double running_sum = 0.0 ;
static unsigned long int CountPowerAboveCP = 0 ; // Count the Power readings above CP
static uint16_t avPower = 0 ; // Average power above CP
const long int NextLevelStep = 1000 ; // Stepsize of the next level of w-prime modification --> 1000 Joules step
static long int NextUpdateLevel = 0 ; // The next level at which to update eCP, e_w_prime_mod and ew_prime_test
// Quarq Dfour Zero Spider power meter sends between 2 and 1.2 power readings per second, dependent of POWER level !!!
// We assume that the sample frequency (number of samples per second) is VARIABLE !!!
// Determine the individual sample time in seconds, it may/will vary during the workout !!!
static unsigned long PrevReadingTime = 0 ;
double SampleTime = double ( millis ()-PrevReadingTime)/ 1000 ; // Time or duration since the previous sample, convert from millis to seconds
PrevReadingTime = millis (); // Update for the next sample
double tau = tau_w_prime_balance (iPower, iCP); // Determine the value for tau
TimeSpent += SampleTime ; // The summed value of all sample time values during the workout
power_above_cp = (iPower - iCP);
# ifdef DEBUGAIR
Serial. printf ( " Time:%6.1f ST: %4.2f tau: %f " , TimeSpent, SampleTime , tau);
# endif
// w_prime is energy and measured in Joules = Watt*second
// Determine the expended energy above CP since the previous measurement (--> i.e. during sample time)
w_prime_expended = double ( max ( 0 , power_above_cp))*SampleTime; // Determine (Watts_above_CP) * (its duration in seconds) = expended energy in Joules!
// Calculate some terms of the equation
ExpTerm1 = exp (TimeSpent/tau); // Exponential term1
ExpTerm2 = exp (-TimeSpent/tau); // Exponential term2
# ifdef DEBUGAIR
Serial. printf ( " W prime expended: %3.0f exp-term1: %f exp-term2: %f " , w_prime_expended , ExpTerm1, ExpTerm2);
# endif
running_sum = running_sum + (w_prime_expended*ExpTerm1); // Determine the running sum
# ifdef DEBUGAIR
Serial. printf ( " Running Sum: %f " , running_sum);
# endif
w_prime_balance = ( long int )( ( double )iw_prime - (running_sum*ExpTerm2) ) ; // Determine w prime balance and cast from double to int
# ifdef DEBUGAIR
Serial. printf ( " w_prime_balance: %d " , w_prime_balance);
# endif
// --------------- extra --------------------------------------------------------------------------------------
// Workout starts at a certain W'= ##,### Joules and CP = ### watts, set by the user; the algorithm increases CP and W' stepwise
// to more realistic values every time when W'balance is depleted to a certain level; -> 2-Parameter Algorithm updates CP and W'
if (power_above_cp > 0 ) {
CalculateAveragePowerAboveCP (iPower, avPower, CountPowerAboveCP); // Average power above CP is to be calculated for future use
T_lim += SampleTime ; // Time to exhaustion: the accurate sum of every second spent above CP, calculated for future use
}
# ifdef DEBUGAIR
Serial. printf ( " [%d] n " , CountPowerAboveCP);
# endif
// When working above CP, the moment comes that we need to update eCP and ew_prime !!
if ( (w_prime_balance < NextUpdateLevel) && (w_prime_expended > 0 ) ) { // W' balance is further depleted --> test for an update moment
NextUpdateLevel -= NextLevelStep; // Move down another level of depletion, update eCP, ew_prime_mod and ew_prime_test
eCP = GetCPfromTwoParameterAlgorithm (avPower, T_lim, iw_prime); // Estimate a new eCP value
ew_prime_mod = w_prime_usr - NextUpdateLevel; // Adjust ew_prime_modified to the next level of depletion to be checked
ew_prime_test = GetWPrimefromTwoParameterAlgorithm ( uint16_t (eCP* 1.045 ), double ( 1200 ), eCP); // 20-Min-test estimate for W-Prime
# ifdef DEBUGAIR
Serial. printf ( " Update of eCP - ew_prime %5d - avPower: %3d - T-lim:%6.1f --> eCP: %3d " , ew_prime_mod, avPower, T_lim, eCP);
Serial. printf ( " --> Test estimate of W-Prime: %d n " , ew_prime_test );
# endif
}
// -----------------extra -------------------------------------------------------------------------------
} // end
// Check and Set starting value of w_prime to realistic numbers!!
void ConstrainW_PrimeValue ( uint16_t &iCP, uint16_t &iw_prime) {
if (iCP < 100 ) { iCP = 100 ; } // Update to lowest level that we allow for
// First determine the "minimal" value for W_Prime according to a 20-min-test estimate, given the iCP value!
uint16_t w_prime_estimate = GetWPrimefromTwoParameterAlgorithm ( uint16_t (iCP* 1.045 ), double ( 1200 ), iCP);
if (iw_prime < w_prime_estimate) { iw_prime = w_prime_estimate; } // Update iw_prime to a realistic level
return ;
} // end
uint16_t GetCPfromTwoParameterAlgorithm ( uint16_t iav_Power, double iT_lim, uint16_t iw_prime) {
uint16_t WprimeDivTlim = uint16_t ( double (iw_prime)/iT_lim ); // type cast for correct calculations
if (iav_Power > WprimeDivTlim){ // test for out of scope
return (iav_Power - WprimeDivTlim); // Solve 2-parameter algorithm to estimate CP
} else {
return eCP; // Something went wrong do'nt allow an update of CP
}
} // end
uint16_t GetWPrimefromTwoParameterAlgorithm ( uint16_t iav_Power, double iT_lim, uint16_t iCP) {
if (iav_Power > iCP){ // test for out of scope
return (iav_Power-iCP)*(( uint16_t )iT_lim); // Solve 2-parameter algorithm to estimate new W-Prime
} else {
return w_prime_usr; // Something went wrong don't allow an update of w_prime
}
} // end
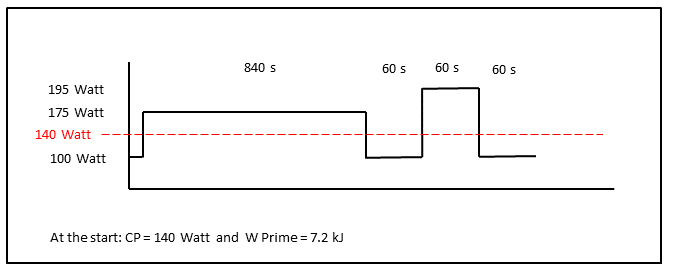
該代碼已集成到一個名為Airffore的較大項目中。設置或更改基礎CP和W Prime是氣流伴侶應用程序不可或缺的一部分!氣流智能設備在室內騎自行車鍛煉的所有階段,熱身,熱身,強度間隔,間歇性恢復和冷卻後,連續調諧冷卻風扇所需的氣流速度以達到穩定的熱量平衡。這位騎自行車的人沒有在線乾擾,可以完全專注於現場培訓師鍛煉的需求,始終面對理想的氣流,使他/她適當地冷卻。此外,騎自行車的人(作為獎勵)洞察力在訓練強度很強烈且足夠長時間時,對他/她的關鍵力量的發展得到了見解!應用的Arduino NRF52480 Express CPU非常強大,以至於可以將CP和W Prime的實時計算完成所有計算,以確定熱量術語,並將風扇置於適當的吹吹動能力。
騎自行車的人(屬性: CP = 140瓦和W Prime = 7.2 kJ )正在進行強烈的鍛煉,如圖所示,持續時間和強度。在第一個間隔塊中, W Prime耗盡了幾次。 CP和W Prime的新值只有在適當的時候才能在鍛煉時間內估算算法。運行視頻以看到W Prime的100%耗竭和實時計算的估計值並在OLED屏幕上顯示...請注意,當功率高於175和195瓦的CP時,水平條如何收縮。該條與w'餘額成正比,此外,“油箱中剩下的東西”還顯示為百分比!讀數以加速序列顯示,不符合鍛煉的持續時間!