Fiquei intrigado com uma publicação que afirmou: é possível medir seu FTP em um minuto em Bikeradar. Mais pesquisando no Google revelou que o Baronbiosys.com desenvolveu um Xert-App que afirma o seguinte:
O método usa técnicas sofisticadas e reconhecimento de padrões para determinar seu FTP. Enquanto no passado você precisava testar usando um protocolo FTP de 20 minutos, por exemplo, ou examinar muitos meses em dados para obter um valor de FTP realista, esse método permite determinar seu FTP naquele dia ou mesmo naquele momento. CF Baronbiosys
Depois de instalar o aplicativo Xert no meu Garmin (830), experimentei, até que o tempo de teste gratuito fosse gasto, que ele faz suas estimativas de FTP notavelmente bem. O Dcrainmaker o revisou e é bastante positivo sobre seu desempenho e precisão e concluiu:
Enquanto aqui é o fato de estar recebendo feedback de FTP em tempo real que é tão único. Eu posso sair para dar um passeio e começar a ver esses valores se formularem enquanto estou dando esforços difíceis. Sem horas de espera, ou até minutos depois. Não estou ciente de nenhuma outra plataforma ou aplicativo que faça isso. CF Dcrainmaker
Decidi desenvolver o código C ++ para um aplicativo de treinamento interno em execução em uma placa expressa Arduino NRF52840 e que chega o mais próximo possível da funcionalidade do aplicativo XERT (para Garmin Connect). Tornou -se parte integrante de um projeto maior: fluxo de ar. A seguir, é apresentada uma explicação da ciência e da matemática por trás de seus fundamentos.
Ficou claro para mim que o aplicativo XERT se baseia no esgotamento da chamada capacidade de trabalho anaeróbica ( AWC ) ou capacidade de reserva funcional ( FRC ). Para simplificar, suponha que um ciclista tenha uma determinada quantidade disso Capacidade de trabalho finito (uma reserva de energia) armazenada internamente no início de um passeio. Essa quantidade de energia é conhecida em termos matemáticos como W ' (Pronounce W Prime ), é energia e, consequentemente, medido em Joules. Enquanto você está montando em baixa intensidade, o W ' permanece em seu nível completo, pois não é gasto, e você pode continuar montando nessa intensidade por um longo tempo. Mas se você se esforçar mais, começará a usar essa energia. O limite em que você começará a gastar esta reserva de energia é conhecida como poder crítico ( CP ). Se você empurrar os pedais mais difícil que o CP , W ' diminuirá. Assim que seu poder produzido (WATTS) ficar menor que o CP , W ' irá "regenerar" e a reserva de energia aumentará novamente. Quando você anda por tempo suficiente abaixo do CP , W ' abordará o nível de 100% novamente. No entanto, quando você trabalha duro e por muito tempo acima do CP , W ' ficará esgotado completamente e você ficará exausto no exato momento (também conhecido como Lim )! As variações em W ' são expressas como " W' Equild " no algoritmo Dr. Skiba (2). Outro parâmetro do algoritmo é a tau que define a velocidade na qual W ' está regenerando quando a energia está abaixo do CP .
A CP é definida como a maior intensidade do exercício que pode ser mantida por períodos prolongados de tempo, normalmente por 45 a 60 min. A potência do limiar funcional ( FTP ) é mais conhecida no ciclo recreativo e foi definido como a maior saída de energia média que pode ser mantida por 60 min (1). Dada a grande semelhança na definição, assumimos que, para ciclismo não elite, a ausência de uma diferença significativa entre os valores de CP e FTP !
Os algoritmos que tiveram que ser implementados são o algoritmo Dr. Skiba original (2) e uma otimização (aproximação) do algoritmo integral skiba por Dave Waterworth (3). O Aart Goossens publicou o Código (em Python) e as informações explicativas no Github (4) que ajudaram muito a entender e implementar os diferentes algoritmos em um ambiente de Arduino. As informações a seguir são parafraseadas de sua obra original, para dar ao leitor algumas dicas sobre o fundo matemático dos algoritmos, veja seu trabalho em: Aart Goosens @ Github
O algoritmo integral skiba é o algoritmo mais conhecido para calcular o equilíbrio de W ' e foi cientificamente validado (5). As equações para o algoritmo são: 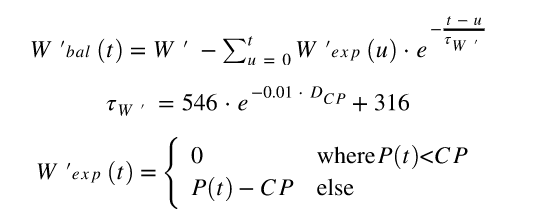
Onde w ' bal (t) é igual a w' bal no tempo t , w ' é a quantidade de energia disponível acima do CP (potência crítica), o tempo para o qual W' bal é calculado, u o iterador do somatório, o tempo de exposição (u) de energia acima do cp que é usado no tempo u ( gasto ) , o número do tempo e o número de tempo e o número de cp. Os números 546, -0,01 e 316 são determinados experimentalmente no artigo original de Skiba e não mudam entre indivíduos. D CP é a diferença entre a CP e a potência média dos intervalos em que a potência estava abaixo do CP . D cp pode ser calculado dinamicamente (a média até o tempo t ) ou calculado uma vez para todo o treino e usado como um valor estático. Skiba recomenda usar um valor estático para D CP . P (t) é o poder produzido no tempo t .
O matemático Dave Waterworth (3) ajudou o desenvolvedor principal de Golden Cheetah, Mark Liversedge, a desenvolver uma otimização do algoritmo Skiba (6). Essa reforma se aproxima do algoritmo Skiba, de modo que os resultados podem variar um pouco apenas em casos extremos, especialmente quando ( tau ) é muito pequeno em comparação com o tempo da amostra. A parte integral de W ' Bal das equações de Skiba é reescrita por Waterworth para: 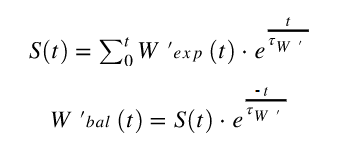
Onde S (t) é uma soma em execução no tempo t Após o início, outros símbolos estão em conformidade com as equações anteriores. Tau (ʈ W ' ) e W' exp (t) são calculados com as equações originais apresentadas por Skiba. O algoritmo integral skiba é bastante caro de calcular, mesmo em computadores rápidos, pois o somatório deve ser repetido para sempre t novamente. A grande vantagem da otimização de Waterworth é que agora o equilíbrio pode ser calculado em tempo real: durante o passeio e não apenas depois! Além disso, é muito útil quando se deseja determinar o poder crítico em tempo real durante os exercícios do HIIT ou exercícios extenuantes quando o equilíbrio de W ' se tornar negativo e se esgotar!
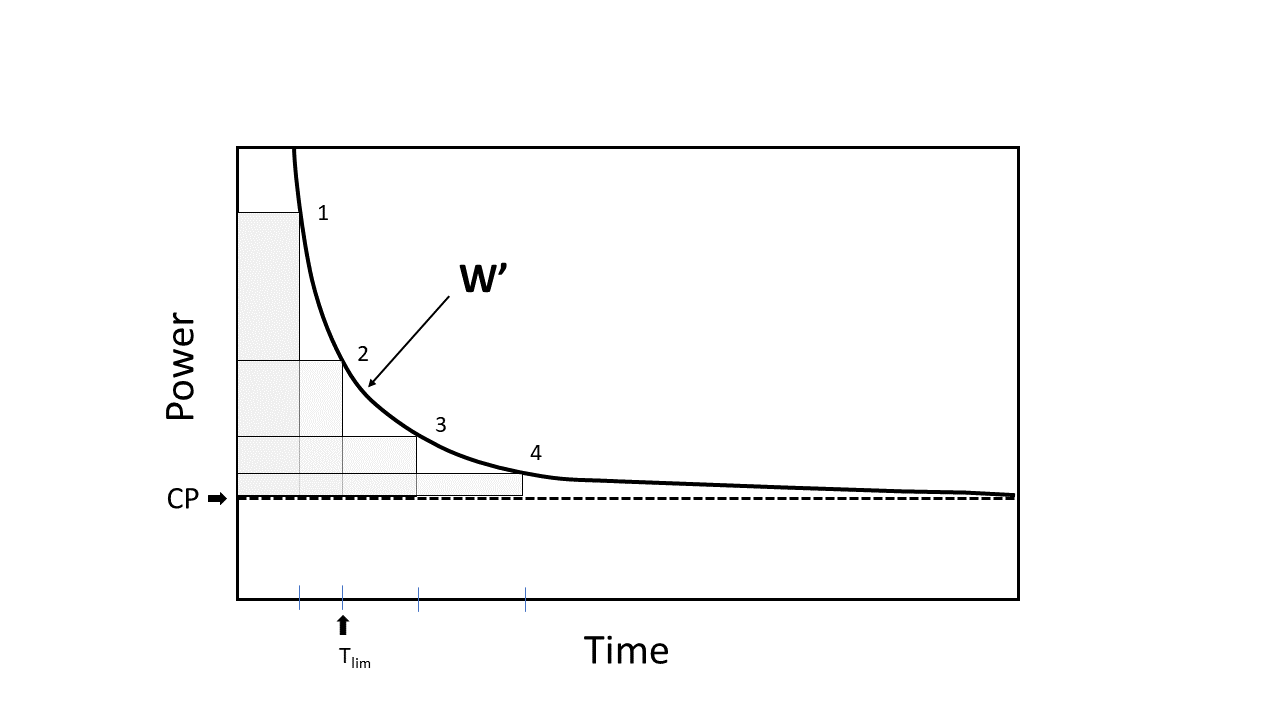
Matematicamente, a relação de potência é descrita como uma função hiperbólica. Os 4 pontos diferentes na curva representam pontos no tempo ( T LIM ) quando ocorre a potência máxima sustentável correspondente acima da CP e ocorre a exaustão. Quando a tolerância ao exercício é considerada, o poder-asimote é conhecido como CP (watts). A constante de curvatura é conhecida como W ' (ou seja, W Prime ), é medida em unidades de trabalho realizado (Joules). Observe que as 4 áreas acinzentadas, representando W ' , são diferentes na forma, mas com aproximadamente tamanho em tamanho. Essa relação hiperbólica de duração da potência pode ser transformada em uma relação linear se o trabalho realizado for plotado contra o tempo, de modo que a inclinação da linha é igual a PC e a interceptação é igual a W ' . Deve-se enfatizar que a relação de potência-duração descreve a tolerância ao exercício, mas não a explica. No entanto, as respostas fisiológicas ao exercício realizadas abaixo e acima da CP podem fornecer informações importantes sobre o processo de fadiga. A CP foi originalmente definida como a potência externa que poderia ser sustentada "indefinidamente" ou por muito tempo sem fadiga. Essa definição deve ser considerada teórica, no entanto, uma vez que nenhum exercício pode ser realizado indefinidamente. Agora se entende que a CP separa as saídas de energia para as quais a tolerância ao exercício é previsivelmente limitada (poder de exercício> CP ). O tempo real para a intolerância ( T LIM ) para o exercício realizado acima da CP é definido e, portanto, previsto de perto pela equação:
T LIM = W ′/(P-CP)
Esta equação destaca que o tempo para a intolerância acima da CP é uma função da proximidade da potência ( P ) sendo sustentada no CP e o tamanho de W ' . Quando P estiver consideravelmente acima da CP , a quantidade constante de trabalho representada pelo parâmetro W ' será utilizada rapidamente e T Lim será curto. Se p estivesse mais próximo do CP , então W ' seria' usado 'mais lentamente e T Lim seria mais longo. Uma consideração crucial aqui é que W ' é assumido como constante para todos os P acima do CP . Esse modelo de tempo de potência ou duração de potência ' dois parâmetros ' implica, portanto, que o desempenho absoluto do exercício depende simplesmente do valor de CP (em watts) e do valor de W ' (em Joules). Os parâmetros CP e W ' podem variar consideravelmente entre os indivíduos em função da saúde/doença, idade, condicionamento físico e treinamento.
// ------------ W' Balance calculation -------------------
// Global variables related to Cycling Power and W-Prime
uint16_t TAWC_Mode = 1 ; // Track Anaerobic Capacity Depletion Mode == TRUE -> APPLY and SHOW
uint16_t CP60 = 160 ; // Your (estimate of) Critical Power, more or less the same as FTP
uint16_t eCP = CP60; // Algorithmic estimate of Critical Power during intense workout
uint16_t w_prime_usr = 7500 ; // Your (estimate of) W-prime or a base value
uint16_t ew_prime_mod = w_prime_usr; // First order estimate of W-prime modified during intense workout
uint16_t ew_prime_test = w_prime_usr; // 20-min-test algorithmic estimate (20 minute @ 5% above eCP) of W-prime for a given eCP!
long int w_prime_balance = 0 ; // Can be negative !!!
bool IsShowWprimeValuesDominant = false ; // Boolean that determines to show W Prime data on Oled or not
// ------------------------------------------------------- // ------------------------ W'Balance Functions -----------------------------------
uint16_t CalculateAveragePowerBelowCP ( uint16_t iPower, uint16_t iCP);
void CalculateAveragePowerAboveCP ( uint16_t iPower, uint16_t &iavPwr, unsigned long &iCpACp);
double tau_w_prime_balance ( uint16_t iPower, uint16_t iCP);
void w_prime_balance_waterworth ( uint16_t iPower, uint16_t iCP, uint16_t iw_prime);
void ConstrainW_PrimeValue ( uint16_t &iCP, uint16_t &iw_prime);
uint16_t GetCPfromTwoParameterAlgorithm ( uint16_t iav_Power, unsigned long iT_lim, uint16_t iw_prime);
uint16_t GetWPrimefromTwoParameterAlgorithm ( uint16_t iav_Power, double iT_lim, uint16_t iCP);
// ------------------------ W'Balance Functions ------------------------------------ uint16_t CalculateAveragePowerBelowCP ( uint16_t iPower, uint16_t iCP){
// calculate avg_power_below_cp real time using a running sum and counter
static unsigned long int CountPowerBelowCP = 0 ;
static unsigned long int SumPowerBelowCP = 0 ;
if (iPower < iCP) {
SumPowerBelowCP += ( unsigned long int )iPower;
CountPowerBelowCP++;
}
return uint16_t (SumPowerBelowCP/CountPowerBelowCP); // average power below CP
} // end calculate avg_power_below_cp
void CalculateAveragePowerAboveCP ( uint16_t iPower, uint16_t &iavPwr, unsigned long int &iCpACp){
// calculate avg_power_above_cp real time using a running sum and counter
// returning the values by C++ reference!
static unsigned long int SumPowerAboveCP = 0 ;
SumPowerAboveCP += ( unsigned long int )iPower;
iCpACp++;
iavPwr = uint16_t (SumPowerAboveCP/iCpACp); // average power above CP
} // end calculate avg_power_above_cp
double tau_w_prime_balance ( uint16_t iPower, uint16_t iCP){
uint16_t avg_power_below_cp = CalculateAveragePowerBelowCP (iPower, iCP);
double delta_cp = double (iCP - avg_power_below_cp);
return ( double ( 546.00 ) * exp (- 0.01 * delta_cp) + double ( 316.00 ));
} // end Tau W Prime Balance
void w_prime_balance_waterworth ( uint16_t iPower, uint16_t iCP, uint16_t iw_prime) {
// Most power meters measure power, torque a.o. in a high frequency (20-60 Hz) but
// transmit (BLE) datasets to a monitoring device in much lower frequency: 1-4 times per second.
int power_above_cp = 0 ; // Power > CP
static double T_lim = 0 ; // Time (duration) while Power is above CP, the summed value of every sample time value P > CP
double w_prime_expended = 0.0 ; // Expended energy in Joules
double ExpTerm1 = 0.0 , ExpTerm2 = 0.0 ;
static double TimeSpent = 0.0 ; // Total Time spent in the workout, the summed value of every sample time value
static double running_sum = 0.0 ;
static unsigned long int CountPowerAboveCP = 0 ; // Count the Power readings above CP
static uint16_t avPower = 0 ; // Average power above CP
const long int NextLevelStep = 1000 ; // Stepsize of the next level of w-prime modification --> 1000 Joules step
static long int NextUpdateLevel = 0 ; // The next level at which to update eCP, e_w_prime_mod and ew_prime_test
// Quarq Dfour Zero Spider power meter sends between 2 and 1.2 power readings per second, dependent of POWER level !!!
// We assume that the sample frequency (number of samples per second) is VARIABLE !!!
// Determine the individual sample time in seconds, it may/will vary during the workout !!!
static unsigned long PrevReadingTime = 0 ;
double SampleTime = double ( millis ()-PrevReadingTime)/ 1000 ; // Time or duration since the previous sample, convert from millis to seconds
PrevReadingTime = millis (); // Update for the next sample
double tau = tau_w_prime_balance (iPower, iCP); // Determine the value for tau
TimeSpent += SampleTime ; // The summed value of all sample time values during the workout
power_above_cp = (iPower - iCP);
# ifdef DEBUGAIR
Serial. printf ( " Time:%6.1f ST: %4.2f tau: %f " , TimeSpent, SampleTime , tau);
# endif
// w_prime is energy and measured in Joules = Watt*second
// Determine the expended energy above CP since the previous measurement (--> i.e. during sample time)
w_prime_expended = double ( max ( 0 , power_above_cp))*SampleTime; // Determine (Watts_above_CP) * (its duration in seconds) = expended energy in Joules!
// Calculate some terms of the equation
ExpTerm1 = exp (TimeSpent/tau); // Exponential term1
ExpTerm2 = exp (-TimeSpent/tau); // Exponential term2
# ifdef DEBUGAIR
Serial. printf ( " W prime expended: %3.0f exp-term1: %f exp-term2: %f " , w_prime_expended , ExpTerm1, ExpTerm2);
# endif
running_sum = running_sum + (w_prime_expended*ExpTerm1); // Determine the running sum
# ifdef DEBUGAIR
Serial. printf ( " Running Sum: %f " , running_sum);
# endif
w_prime_balance = ( long int )( ( double )iw_prime - (running_sum*ExpTerm2) ) ; // Determine w prime balance and cast from double to int
# ifdef DEBUGAIR
Serial. printf ( " w_prime_balance: %d " , w_prime_balance);
# endif
// --------------- extra --------------------------------------------------------------------------------------
// Workout starts at a certain W'= ##,### Joules and CP = ### watts, set by the user; the algorithm increases CP and W' stepwise
// to more realistic values every time when W'balance is depleted to a certain level; -> 2-Parameter Algorithm updates CP and W'
if (power_above_cp > 0 ) {
CalculateAveragePowerAboveCP (iPower, avPower, CountPowerAboveCP); // Average power above CP is to be calculated for future use
T_lim += SampleTime ; // Time to exhaustion: the accurate sum of every second spent above CP, calculated for future use
}
# ifdef DEBUGAIR
Serial. printf ( " [%d] n " , CountPowerAboveCP);
# endif
// When working above CP, the moment comes that we need to update eCP and ew_prime !!
if ( (w_prime_balance < NextUpdateLevel) && (w_prime_expended > 0 ) ) { // W' balance is further depleted --> test for an update moment
NextUpdateLevel -= NextLevelStep; // Move down another level of depletion, update eCP, ew_prime_mod and ew_prime_test
eCP = GetCPfromTwoParameterAlgorithm (avPower, T_lim, iw_prime); // Estimate a new eCP value
ew_prime_mod = w_prime_usr - NextUpdateLevel; // Adjust ew_prime_modified to the next level of depletion to be checked
ew_prime_test = GetWPrimefromTwoParameterAlgorithm ( uint16_t (eCP* 1.045 ), double ( 1200 ), eCP); // 20-Min-test estimate for W-Prime
# ifdef DEBUGAIR
Serial. printf ( " Update of eCP - ew_prime %5d - avPower: %3d - T-lim:%6.1f --> eCP: %3d " , ew_prime_mod, avPower, T_lim, eCP);
Serial. printf ( " --> Test estimate of W-Prime: %d n " , ew_prime_test );
# endif
}
// -----------------extra -------------------------------------------------------------------------------
} // end
// Check and Set starting value of w_prime to realistic numbers!!
void ConstrainW_PrimeValue ( uint16_t &iCP, uint16_t &iw_prime) {
if (iCP < 100 ) { iCP = 100 ; } // Update to lowest level that we allow for
// First determine the "minimal" value for W_Prime according to a 20-min-test estimate, given the iCP value!
uint16_t w_prime_estimate = GetWPrimefromTwoParameterAlgorithm ( uint16_t (iCP* 1.045 ), double ( 1200 ), iCP);
if (iw_prime < w_prime_estimate) { iw_prime = w_prime_estimate; } // Update iw_prime to a realistic level
return ;
} // end
uint16_t GetCPfromTwoParameterAlgorithm ( uint16_t iav_Power, double iT_lim, uint16_t iw_prime) {
uint16_t WprimeDivTlim = uint16_t ( double (iw_prime)/iT_lim ); // type cast for correct calculations
if (iav_Power > WprimeDivTlim){ // test for out of scope
return (iav_Power - WprimeDivTlim); // Solve 2-parameter algorithm to estimate CP
} else {
return eCP; // Something went wrong do'nt allow an update of CP
}
} // end
uint16_t GetWPrimefromTwoParameterAlgorithm ( uint16_t iav_Power, double iT_lim, uint16_t iCP) {
if (iav_Power > iCP){ // test for out of scope
return (iav_Power-iCP)*(( uint16_t )iT_lim); // Solve 2-parameter algorithm to estimate new W-Prime
} else {
return w_prime_usr; // Something went wrong don't allow an update of w_prime
}
} // end
O código foi integrado em um projeto maior chamado fluxo de ar . Definir ou alterar seu CP basal e W Prime são parte integrante de um aplicativo complementar do fluxo de ar ! O dispositivo Smart Airflow sintoniza continuamente a velocidade solicitada do fluxo de ar dos ventiladores de resfriamento para um equilíbrio de calor estável durante todas as fases de um treino de ciclismo interior, intervalos de aquecimento, intensidade, recuperação intermitente e em recarga. O ciclista não tem interferência em andamento e pode se concentrar totalmente nas demandas do treino de treinadores de papelay, sempre enfrentando o Airstream ideal que o esfriará adequadamente. Além disso, os ciclistas recebem uma visão (como um bônus) no desenvolvimento de seu poder crítico quando a intensidade do treinamento é intensa e longa o suficiente! A CPU Applied Arduino NRF52480 Express é tão poderosa que o cálculo em tempo real de CP e W Prime pode ser realizado de lado todos os cálculos para determinar os termos do balanço de calor e definir os ventiladores na capacidade de sopro apropriada.
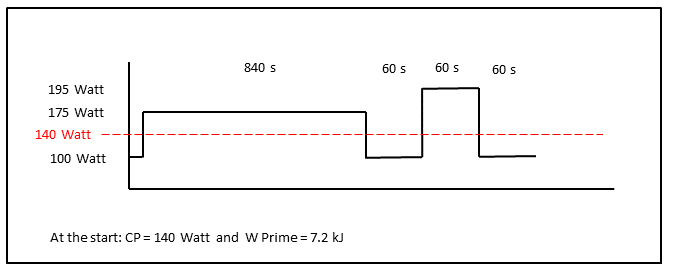
Um ciclista (propriedades: cp = 140 watts e w prime = 7,2 kJ ) está fazendo um treino intenso com a duração e a intensidade, como mostrado na figura. W Prime é esgotado várias vezes durante o primeiro bloqueio de intervalo. Novos valores para CP e W Prime serão estimados pelo algoritmo durante o tempo de treino somente quando apropriado. Execute o vídeo para ver 100% de depleção do W Prime e os valores estimados, pois foram calculados em tempo real e apresentados em uma tela OLED ... Observe como a barra horizontal encolhe quando a energia está acima do CP em 175 e 195 watts. A barra é proporcional com o equilíbrio de W ' e, além disso, o que é "deixado no tanque" é mostrado como uma porcentagem! As leituras são mostradas em uma sequência acumulada e não estão em conformidade com a duração do tempo do treino!