Saya bingung dengan publikasi yang mengklaim: dimungkinkan untuk mengukur FTP Anda dalam satu menit di Bikeradar. Googling lebih lanjut mengungkapkan bahwa baronbiosys.com mengembangkan XERT-APP yang mengklaim ini:
Metode ini menggunakan teknik canggih dan pengenalan pola untuk menentukan FTP Anda. Sedangkan di masa lalu Anda perlu menguji menggunakan protokol FTP 20 menit misalnya, atau memeriksa data senilai berbulan -bulan untuk mendapatkan nilai FTP yang realistis, metode ini memungkinkan Anda untuk menentukan FTP Anda pada hari itu atau bahkan pada saat itu. CF BARONBIOSYS
Setelah menginstal aplikasi XERT di Garmin saya (830), saya telah mengalami, sampai waktu uji coba gratis dikeluarkan, bahwa ia melakukan perkiraan FTP dengan sangat baik. DCRAINMAKER mengulasnya dan cukup positif tentang kinerja dan akurasinya dan menyimpulkan:
Sedangkan di sini adalah fakta bahwa saya mendapatkan umpan balik FTP secara real-time yang sangat unik. Saya bisa keluar untuk naik dan mulai melihat nilai -nilai ini merumuskan saat saya memberikan upaya keras. Tidak ada jam menunggu, atau bahkan beberapa menit kemudian. Saya tidak mengetahui adanya platform atau aplikasi lain yang melakukan itu. CF DCRAINMAKER
Saya memutuskan untuk mengembangkan kode C ++ untuk aplikasi pelatihan dalam ruangan yang berjalan pada papan Express Arduino NRF52840 dan yang sedekat mungkin dengan fungsionalitas aplikasi XERT (untuk Garmin Connect). Itu menjadi bagian integral dari proyek yang lebih besar: aliran udara. Berikut ini adalah penjelasan tentang sains dan matematika di balik fundamentalnya.
Jelas bagi saya bahwa aplikasi XERT didasarkan pada penipisan apa yang disebut kapasitas kerja anaerob ( AWC ) atau kapasitas cadangan fungsional ( FRC ). Agar tetap sederhana, asumsikan bahwa pengendara sepeda memiliki jumlah ini kapasitas kerja yang terbatas (Cadangan energi) disimpan secara internal di awal perjalanan. Jumlah energi ini diketahui dalam istilah matematika sebagai w ' (ucapan prime ), itu adalah energi dan akibatnya diukur dalam joule. Saat Anda mengendarai dengan intensitas rendah, W ' tetap pada level penuh karena tidak dikeluarkan, dan Anda dapat terus mengendarai intensitas ini untuk waktu yang lama. Tetapi jika Anda mendorong lebih keras, Anda akan mulai menggunakan energi ini. Batas di mana Anda akan mulai mengeluarkan cadangan energi ini dikenal sebagai Power Critical ( CP ). Jika Anda mendorong pedal lebih keras dari CP , W ' akan berkurang. Segera setelah daya yang Anda hasilkan (watt) semakin rendah dari CP , W ' akan "beregenerasi", dan cadangan energi akan meningkat lagi. Saat Anda berkendara cukup lama di bawah CP , W ' akan mendekati level 100% lagi. Namun, ketika Anda bekerja keras dan cukup lama di atas CP , W ' akan habis sepenuhnya dan Anda akan kelelahan pada saat itu (alias t lim )! Variasi dalam W ' dinyatakan sebagai " w' keseimbangan " dalam algoritma Dr. Skiba (2). Parameter lain dari algoritma adalah tau yang mendefinisikan kecepatan di mana W ' regenerasi ketika daya di bawah CP .
CP didefinisikan sebagai intensitas latihan tertinggi yang dapat dipertahankan untuk periode waktu yang lama, biasanya selama 45 hingga 60 menit. Functional Threshold Power ( FTP ) lebih terkenal dalam bersepeda rekreasi dan telah didefinisikan sebagai output daya rata-rata tertinggi yang dapat dipertahankan selama 60 menit (1). Mengingat kesamaan besar dalam definisi, kami mengasumsikan untuk bersepeda non-elit, tidak adanya perbedaan yang signifikan antara nilai CP dan FTP !
Algoritma yang harus diimplementasikan adalah algoritma Dr. Skiba asli (2) dan optimasi (perkiraan) dari algoritma Skiba integral oleh Dave Waterworth (3). Aart Goossens yang diterbitkan kode (dalam Python) dan informasi penjelasan tentang GitHub (4) yang banyak membantu memahami dan mengimplementasikan berbagai algoritma dalam pengaturan Arduino. Informasi berikut diparafrasekan dari karya aslinya, untuk memberi pembaca wawasan tentang latar belakang matematika algoritma, lihat karyanya di: aart goosens @ github
Algoritma Skiba Integral adalah algoritma paling terkenal untuk menghitung keseimbangan W ' dan telah divalidasi secara ilmiah (5). Persamaan untuk algoritma adalah: 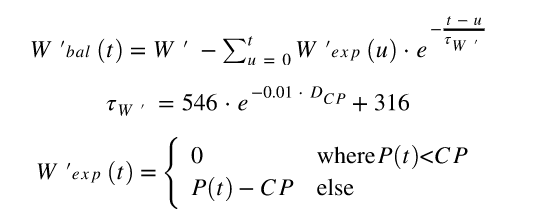
Di mana w ' bal (t) sama dengan w' bal pada waktu t , w ' adalah jumlah energi yang tersedia di atas cp (kekuatan kritis), t waktu yang dihitung, u iterator penjumlahan, w' exp (u) jumlah energi di atas cp yang digunakan pada waktu u ( dikeluarkan ), e expen . Angka 546, -0,01 dan 316 ditentukan secara eksperimental dalam artikel asli Skiba dan tidak berubah antar individu. D CP adalah perbedaan antara CP dan kekuatan rata -rata interval di mana daya di bawah CP . D CP dapat dihitung secara dinamis (rata -rata sampai waktu t ) atau dihitung sekali untuk seluruh latihan dan digunakan sebagai nilai statis. Skiba merekomendasikan menggunakan nilai statis untuk D CP . P (t) adalah kekuatan yang dihasilkan pada waktu t .
Matematikawan Dave Waterworth (3) membantu pengembang inti Golden Cheetah, Mark Liversedge, untuk mengembangkan optimalisasi algoritma Skiba (6). Reformulasi ini mendekati algoritma Skiba sehingga hasilnya dapat sedikit bervariasi dalam kasus ekstrem saja, terutama ketika ( tau ) sangat kecil dibandingkan dengan waktu sampel. Bagian integral dari persamaan Skiba ditulis ulang oleh Waterworth untuk: 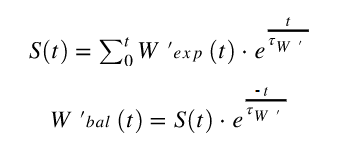
Di mana s (t) adalah jumlah berjalan pada waktu t setelah awal, simbol lain menyesuaikan persamaan sebelumnya. Tau (ʈ w ' ) dan w' exp (t) dihitung dengan persamaan asli yang disajikan oleh Skiba. Algoritma Skiba Integral cukup mahal untuk dihitung, bahkan pada komputer cepat karena penjumlahan harus diulang untuk setiap kali t lagi. Keuntungan besar dari optimasi Waterworth adalah bahwa sekarang keseimbangan dapat dihitung secara real time: selama perjalanan dan tidak hanya sesudahnya! Selain itu, sangat membantu ketika seseorang ingin menentukan kekuatan kritis dengan cepat selama latihan HIIT atau latihan berat ketika keseimbangan W ' menjadi negatif dan telah habis!
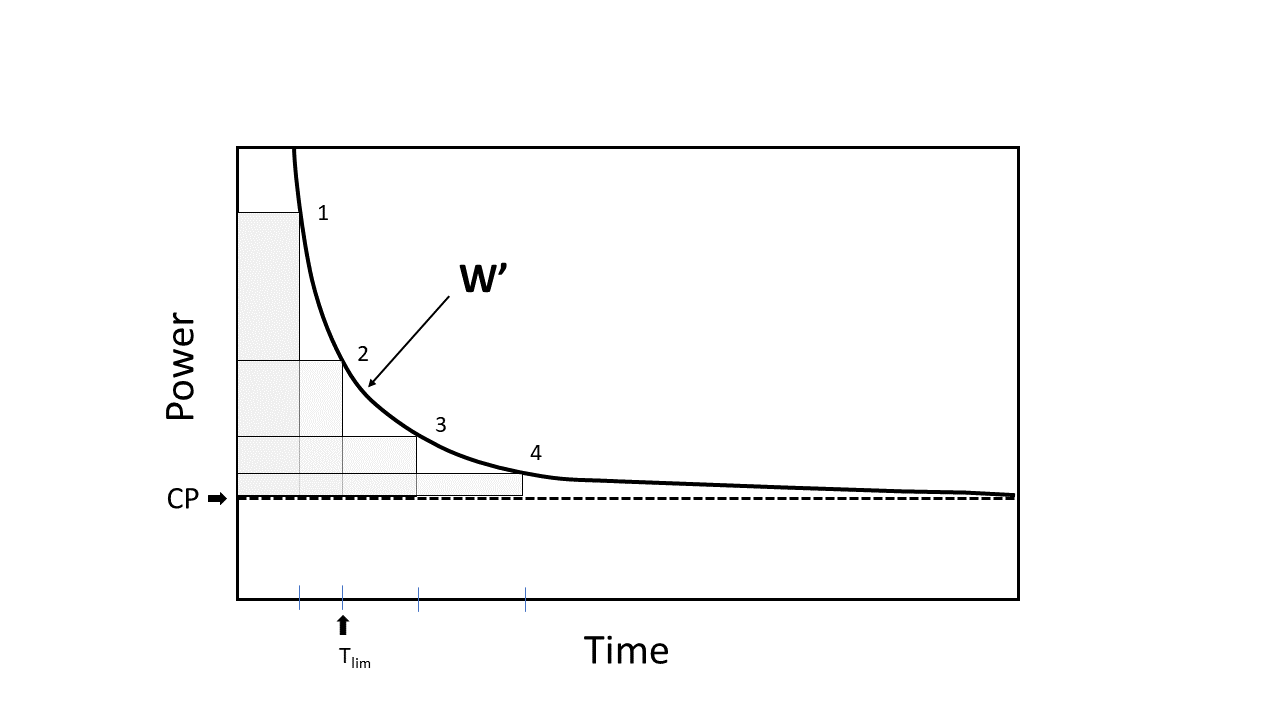
Secara matematis, hubungan durasi daya digambarkan sebagai fungsi hiperbolik. 4 titik berbeda pada kurva mewakili titik waktu ( t lim ) ketika sesuai dengan daya berkelanjutan maksimum di atas CP tercapai dan kelelahan terjadi. Ketika toleransi olahraga dipertimbangkan, power-asymptote dikenal sebagai CP (Watts). Konstanta kelengkungan dikenal sebagai W ' (yaitu, w prime ), diukur dalam satuan pekerjaan yang dilakukan (joule). Perhatikan bahwa 4 area abu -abu, mewakili W ' , berbeda dalam bentuk tetapi sekitar ukuran yang sama. Hubungan durasi daya hiperbolik ini dapat diubah menjadi hubungan linier jika pekerjaan yang dilakukan diplot terhadap waktu, sehingga kemiringan garis sama dengan CP dan intersep sama dengan W ' . Harus ditekankan bahwa hubungan durasi daya menggambarkan toleransi olahraga tetapi tidak menjelaskannya. Namun demikian, respons fisiologis terhadap olahraga yang dilakukan di bawah dan di atas CP dapat memberikan wawasan penting tentang proses kelelahan. CP awalnya didefinisikan sebagai output daya eksternal yang dapat dipertahankan "tanpa batas waktu" atau untuk waktu yang sangat lama tanpa kelelahan. Namun, definisi ini harus dianggap teoretis, karena tidak ada latihan yang dapat dilakukan tanpa batas waktu. Sekarang dipahami bahwa CP memisahkan output daya yang toleransi olahraga dapat diprediksi terbatas (Latihan Daya> CP ). Waktu aktual untuk intoleransi ( t lim ) untuk olahraga yang dilakukan di atas CP didefinisikan, dan karenanya diprediksi erat, dengan persamaan:
T lim = w ′/(p-cp)
Persamaan ini menyoroti bahwa waktu untuk intoleransi di atas CP adalah fungsi dari kedekatan output daya ( p ) yang dipertahankan untuk CP dan ukuran W ' . Ketika P jauh di atas CP , jumlah konstan pekerjaan yang diwakili oleh parameter W ' akan digunakan dengan cepat dan T Lim akan pendek. Jika P lebih dekat ke CP , maka W ' akan' digunakan 'lebih lambat dan L Lim akan lebih lama. Pertimbangan penting di sini adalah bahwa W ' diasumsikan konstan untuk semua P di atas CP . Oleh karena itu, model waktu daya atau durasi daya ' dua parameter ' ini menyiratkan bahwa kinerja latihan absolut hanya bergantung pada nilai CP (dalam watt) dan nilai W ' (dalam joule). Parameter CP dan W ' dapat sangat bervariasi di antara individu sebagai fungsi kesehatan/penyakit, usia, kebugaran, dan pelatihan.
// ------------ W' Balance calculation -------------------
// Global variables related to Cycling Power and W-Prime
uint16_t TAWC_Mode = 1 ; // Track Anaerobic Capacity Depletion Mode == TRUE -> APPLY and SHOW
uint16_t CP60 = 160 ; // Your (estimate of) Critical Power, more or less the same as FTP
uint16_t eCP = CP60; // Algorithmic estimate of Critical Power during intense workout
uint16_t w_prime_usr = 7500 ; // Your (estimate of) W-prime or a base value
uint16_t ew_prime_mod = w_prime_usr; // First order estimate of W-prime modified during intense workout
uint16_t ew_prime_test = w_prime_usr; // 20-min-test algorithmic estimate (20 minute @ 5% above eCP) of W-prime for a given eCP!
long int w_prime_balance = 0 ; // Can be negative !!!
bool IsShowWprimeValuesDominant = false ; // Boolean that determines to show W Prime data on Oled or not
// ------------------------------------------------------- // ------------------------ W'Balance Functions -----------------------------------
uint16_t CalculateAveragePowerBelowCP ( uint16_t iPower, uint16_t iCP);
void CalculateAveragePowerAboveCP ( uint16_t iPower, uint16_t &iavPwr, unsigned long &iCpACp);
double tau_w_prime_balance ( uint16_t iPower, uint16_t iCP);
void w_prime_balance_waterworth ( uint16_t iPower, uint16_t iCP, uint16_t iw_prime);
void ConstrainW_PrimeValue ( uint16_t &iCP, uint16_t &iw_prime);
uint16_t GetCPfromTwoParameterAlgorithm ( uint16_t iav_Power, unsigned long iT_lim, uint16_t iw_prime);
uint16_t GetWPrimefromTwoParameterAlgorithm ( uint16_t iav_Power, double iT_lim, uint16_t iCP);
// ------------------------ W'Balance Functions ------------------------------------ uint16_t CalculateAveragePowerBelowCP ( uint16_t iPower, uint16_t iCP){
// calculate avg_power_below_cp real time using a running sum and counter
static unsigned long int CountPowerBelowCP = 0 ;
static unsigned long int SumPowerBelowCP = 0 ;
if (iPower < iCP) {
SumPowerBelowCP += ( unsigned long int )iPower;
CountPowerBelowCP++;
}
return uint16_t (SumPowerBelowCP/CountPowerBelowCP); // average power below CP
} // end calculate avg_power_below_cp
void CalculateAveragePowerAboveCP ( uint16_t iPower, uint16_t &iavPwr, unsigned long int &iCpACp){
// calculate avg_power_above_cp real time using a running sum and counter
// returning the values by C++ reference!
static unsigned long int SumPowerAboveCP = 0 ;
SumPowerAboveCP += ( unsigned long int )iPower;
iCpACp++;
iavPwr = uint16_t (SumPowerAboveCP/iCpACp); // average power above CP
} // end calculate avg_power_above_cp
double tau_w_prime_balance ( uint16_t iPower, uint16_t iCP){
uint16_t avg_power_below_cp = CalculateAveragePowerBelowCP (iPower, iCP);
double delta_cp = double (iCP - avg_power_below_cp);
return ( double ( 546.00 ) * exp (- 0.01 * delta_cp) + double ( 316.00 ));
} // end Tau W Prime Balance
void w_prime_balance_waterworth ( uint16_t iPower, uint16_t iCP, uint16_t iw_prime) {
// Most power meters measure power, torque a.o. in a high frequency (20-60 Hz) but
// transmit (BLE) datasets to a monitoring device in much lower frequency: 1-4 times per second.
int power_above_cp = 0 ; // Power > CP
static double T_lim = 0 ; // Time (duration) while Power is above CP, the summed value of every sample time value P > CP
double w_prime_expended = 0.0 ; // Expended energy in Joules
double ExpTerm1 = 0.0 , ExpTerm2 = 0.0 ;
static double TimeSpent = 0.0 ; // Total Time spent in the workout, the summed value of every sample time value
static double running_sum = 0.0 ;
static unsigned long int CountPowerAboveCP = 0 ; // Count the Power readings above CP
static uint16_t avPower = 0 ; // Average power above CP
const long int NextLevelStep = 1000 ; // Stepsize of the next level of w-prime modification --> 1000 Joules step
static long int NextUpdateLevel = 0 ; // The next level at which to update eCP, e_w_prime_mod and ew_prime_test
// Quarq Dfour Zero Spider power meter sends between 2 and 1.2 power readings per second, dependent of POWER level !!!
// We assume that the sample frequency (number of samples per second) is VARIABLE !!!
// Determine the individual sample time in seconds, it may/will vary during the workout !!!
static unsigned long PrevReadingTime = 0 ;
double SampleTime = double ( millis ()-PrevReadingTime)/ 1000 ; // Time or duration since the previous sample, convert from millis to seconds
PrevReadingTime = millis (); // Update for the next sample
double tau = tau_w_prime_balance (iPower, iCP); // Determine the value for tau
TimeSpent += SampleTime ; // The summed value of all sample time values during the workout
power_above_cp = (iPower - iCP);
# ifdef DEBUGAIR
Serial. printf ( " Time:%6.1f ST: %4.2f tau: %f " , TimeSpent, SampleTime , tau);
# endif
// w_prime is energy and measured in Joules = Watt*second
// Determine the expended energy above CP since the previous measurement (--> i.e. during sample time)
w_prime_expended = double ( max ( 0 , power_above_cp))*SampleTime; // Determine (Watts_above_CP) * (its duration in seconds) = expended energy in Joules!
// Calculate some terms of the equation
ExpTerm1 = exp (TimeSpent/tau); // Exponential term1
ExpTerm2 = exp (-TimeSpent/tau); // Exponential term2
# ifdef DEBUGAIR
Serial. printf ( " W prime expended: %3.0f exp-term1: %f exp-term2: %f " , w_prime_expended , ExpTerm1, ExpTerm2);
# endif
running_sum = running_sum + (w_prime_expended*ExpTerm1); // Determine the running sum
# ifdef DEBUGAIR
Serial. printf ( " Running Sum: %f " , running_sum);
# endif
w_prime_balance = ( long int )( ( double )iw_prime - (running_sum*ExpTerm2) ) ; // Determine w prime balance and cast from double to int
# ifdef DEBUGAIR
Serial. printf ( " w_prime_balance: %d " , w_prime_balance);
# endif
// --------------- extra --------------------------------------------------------------------------------------
// Workout starts at a certain W'= ##,### Joules and CP = ### watts, set by the user; the algorithm increases CP and W' stepwise
// to more realistic values every time when W'balance is depleted to a certain level; -> 2-Parameter Algorithm updates CP and W'
if (power_above_cp > 0 ) {
CalculateAveragePowerAboveCP (iPower, avPower, CountPowerAboveCP); // Average power above CP is to be calculated for future use
T_lim += SampleTime ; // Time to exhaustion: the accurate sum of every second spent above CP, calculated for future use
}
# ifdef DEBUGAIR
Serial. printf ( " [%d] n " , CountPowerAboveCP);
# endif
// When working above CP, the moment comes that we need to update eCP and ew_prime !!
if ( (w_prime_balance < NextUpdateLevel) && (w_prime_expended > 0 ) ) { // W' balance is further depleted --> test for an update moment
NextUpdateLevel -= NextLevelStep; // Move down another level of depletion, update eCP, ew_prime_mod and ew_prime_test
eCP = GetCPfromTwoParameterAlgorithm (avPower, T_lim, iw_prime); // Estimate a new eCP value
ew_prime_mod = w_prime_usr - NextUpdateLevel; // Adjust ew_prime_modified to the next level of depletion to be checked
ew_prime_test = GetWPrimefromTwoParameterAlgorithm ( uint16_t (eCP* 1.045 ), double ( 1200 ), eCP); // 20-Min-test estimate for W-Prime
# ifdef DEBUGAIR
Serial. printf ( " Update of eCP - ew_prime %5d - avPower: %3d - T-lim:%6.1f --> eCP: %3d " , ew_prime_mod, avPower, T_lim, eCP);
Serial. printf ( " --> Test estimate of W-Prime: %d n " , ew_prime_test );
# endif
}
// -----------------extra -------------------------------------------------------------------------------
} // end
// Check and Set starting value of w_prime to realistic numbers!!
void ConstrainW_PrimeValue ( uint16_t &iCP, uint16_t &iw_prime) {
if (iCP < 100 ) { iCP = 100 ; } // Update to lowest level that we allow for
// First determine the "minimal" value for W_Prime according to a 20-min-test estimate, given the iCP value!
uint16_t w_prime_estimate = GetWPrimefromTwoParameterAlgorithm ( uint16_t (iCP* 1.045 ), double ( 1200 ), iCP);
if (iw_prime < w_prime_estimate) { iw_prime = w_prime_estimate; } // Update iw_prime to a realistic level
return ;
} // end
uint16_t GetCPfromTwoParameterAlgorithm ( uint16_t iav_Power, double iT_lim, uint16_t iw_prime) {
uint16_t WprimeDivTlim = uint16_t ( double (iw_prime)/iT_lim ); // type cast for correct calculations
if (iav_Power > WprimeDivTlim){ // test for out of scope
return (iav_Power - WprimeDivTlim); // Solve 2-parameter algorithm to estimate CP
} else {
return eCP; // Something went wrong do'nt allow an update of CP
}
} // end
uint16_t GetWPrimefromTwoParameterAlgorithm ( uint16_t iav_Power, double iT_lim, uint16_t iCP) {
if (iav_Power > iCP){ // test for out of scope
return (iav_Power-iCP)*(( uint16_t )iT_lim); // Solve 2-parameter algorithm to estimate new W-Prime
} else {
return w_prime_usr; // Something went wrong don't allow an update of w_prime
}
} // end
Kode ini telah diintegrasikan dalam proyek yang lebih besar yang disebut Airflow . Mengatur atau mengubah CP basal Anda dan W Prime adalah bagian integral dari aplikasi pendamping aliran udara ! Perangkat pintar aliran udara terus-menerus menyetel kecepatan aliran udara yang diminta dari kipas pendingin untuk keseimbangan panas yang stabil selama semua fase latihan bersepeda dalam ruangan, pemanasan, interval intensitas, pemulihan intermiten dan di cooldown. Pengendara sepeda tidak memiliki gangguan di jalan dan dapat berkonsentrasi penuh pada tuntutan latihan pelatih stationay, selalu menghadapi aliran udara ideal yang akan mendinginkannya dengan tepat. Selain itu, pengendara sepeda mendapatkan (sebagai bonus) wawasan dalam pengembangan kekuatan kritisnya ketika intensitas pelatihan intens dan cukup lama! Arduino NRF52480 Express CPU yang diterapkan sangat kuat sehingga perhitungan waktu nyata CP dan W Prime dapat dicapai selain semua perhitungan untuk menentukan istilah keseimbangan panas dan mengatur kipas ke kapasitas peniup yang sesuai.
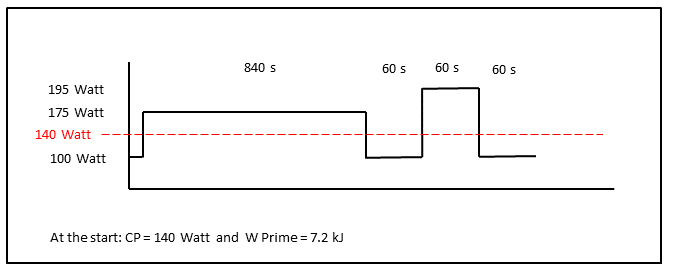
Pengendara sepeda (Properti: CP = 140 watt dan W Prime = 7,2 kJ ) sedang melakukan latihan yang intens dengan durasi dan intensitas seperti yang ditunjukkan pada gambar. W Prime habis beberapa kali selama blok interval pertama. Nilai baru untuk CP dan W Prime akan diperkirakan oleh algoritma selama waktu latihan hanya jika perlu. Jalankan video untuk melihat penipisan 100% dari W Prime dan nilai -nilai yang diperkirakan saat mereka dihitung secara real time dan disajikan pada layar OLED ... Perhatikan bagaimana bilah horizontal menyusut ketika daya di atas CP pada 175 dan 195 watt. Bilah proporsional dengan keseimbangan W ' dan di samping itu apa yang "ditinggalkan di dalam tangki" ditampilkan sebagai persentase! Bacaan ditunjukkan dalam urutan terakerat dan tidak sesuai dengan durasi waktu yang ditunjukkan dari latihan!