J'ai été perplexe par une publication qui prétendait: il est possible de mesurer votre FTP en une minute à Bikeradar. Plus loin sur Google a révélé que Baronbiosys.com a développé une application Xert qui le prétend:
La méthode utilise des techniques sophistiquées et une reconnaissance de motifs pour déterminer votre FTP. Alors que dans le passé, vous deviez soit tester à l'aide d'un protocole FTP de 20 minutes par exemple, ou examiner la valeur de plusieurs mois de données pour obtenir une valeur FTP réaliste, cette méthode vous permet de déterminer votre FTP ce jour-là ou même à ce moment-là. CF Baronbiosys
Après avoir installé l' application Xert sur mon Garmin (830), j'ai vécu, jusqu'à ce que le temps d'essai gratuit soit dépensé, qu'il fait remarquablement bien ses estimations de FTP . DCRAINMAKER l'a examiné et est assez positif quant à ses performances et à sa précision et a conclu:
Alors que ici, c'est le fait que j'obtiens des commentaires FTP en temps réel qui sont si uniques. Je peux sortir faire un tour et commencer à voir ces valeurs formuler car je fais des efforts difficiles. Pas d'heures d'attente, voire quelques minutes plus tard. Je ne connais aucune autre plate-forme ou application qui le fait. CF DCRAINMAKER
J'ai décidé de développer un code C ++ pour une application de formation en intérieur qui s'exécute sur une carte Arduino NRF52840 Express et qui s'approche le plus possible de la fonctionnalité de l' application Xert (pour Garmin Connect). Il est devenu une partie intégrante d'un projet plus grand: le flux d'air. Ce qui suit est une explication des sciences et des mathématiques derrière ses principes fondamentaux.
Il était clair pour moi que l' application Xert est basée sur l'épuisement de la capacité de travail dite anaérobie ( AWC ) ou de la capacité de réserve fonctionnelle ( FRC ). Pour rester simple, supposons qu'un cycliste en a une quantité donnée capacité de travail finie (une réserve d'énergie) stocké en interne au début d'un trajet. Cette quantité d'énergie est connue en termes mathématiques comme w ' (prononcer w prime ), il est de l'énergie et par conséquent mesuré en Joules. Pendant que vous roulez à une faible intensité, il reste à son niveau complet car il n'est pas dépensé et vous pouvez continuer à rouler à cette intensité pendant longtemps. Mais si vous poussez plus fort, vous commencerez à utiliser cette énergie. La limite à laquelle vous commencerez à dépenser cette réserve d'énergie est connue sous le nom de puissance critique ( CP ). Si vous poussez les pédales plus durs que CP , W '' diminuera. Dès que votre puissance produite (watts) est inférieure à celle du CP , nous «régénérera» et la réserve d'énergie augmentera à nouveau. Lorsque vous roulez assez longtemps en dessous du CP , W '« va à nouveau approcher le niveau à 100%. Cependant, lorsque vous travaillez dur et assez longtemps au-dessus du CP , il sera complètement épuisé et vous serez épuisé au moment même (aka t lim )! Les variations de W ' sont exprimées en « W' Balance » dans l'algorithme du Dr Skiba (2). Un autre paramètre de l'algorithme est Tau qui définit la vitesse à laquelle W ' se régénère lorsque la puissance est en dessous du CP .
Le CP est défini comme l'intensité d'exercice la plus élevée qui peut être maintenue pendant des périodes prolongées, généralement pendant 45 à 60 min. La puissance de seuil fonctionnelle ( FTP ) est plus connue dans le cycle récréatif et a été définie comme la puissance moyenne la plus élevée qui peut être maintenue pendant 60 min (1). Compte tenu de la grande similitude dans la définition, nous supposons pour le cyclisme non élite de l'absence d'une différence significative entre les valeurs CP et FTP !
Les algorithmes qui ont dû être mis en œuvre sont l'algorithme original du Dr Skiba (2) et une optimisation (approximation) de l'algorithme de skiba intégral par Dave Waterworth (3). Le code publié AART GOOSSENS (dans Python) et des informations explicatives sur GitHub (4) qui ont beaucoup aidé à comprendre et à implémenter les différents algorithmes dans un paramètre Arduino. Les informations suivantes sont paraphrasées de son travail original, pour donner au lecteur un aperçu de l'arrière-plan mathématique des algorithmes, voir son travail à: aart goosens @ github
L'algorithme de skiba intégral est l'algorithme le plus connu pour calculer l'équilibre de W ' et a été scientifiquement validé (5). Les équations de l'algorithme sont: 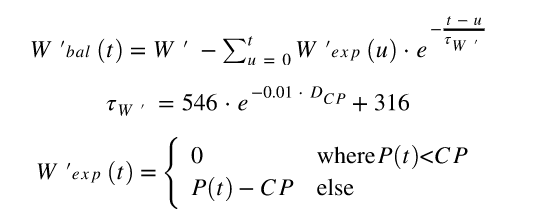
Lorsque w ' Bal (t) est égal à W' Bal au temps t , w ' est la quantité d'énergie disponible au-dessus de CP (puissance critique), le temps pour lequel w' Bal est calculé, u le itérateur de la sommation, la quantité d'énergie exp (u) au-dessus de CP qui est utilisée à un temps u (dépensé), e le nombre d'Euler et ʈ w ' (prononcé Tau ) Une constante de temps qui décrit la vitesse d'Euler. Les nombres 546, -0,01 et 316 sont déterminés expérimentalement dans l'article original de Skiba et ne changent pas entre les individus. D CP est la différence entre CP et la puissance moyenne des intervalles dans lesquels la puissance était inférieure à CP . D cp Peut être calculé dynamiquement (la moyenne jusqu'au temps t ) ou calculé une fois pour l'ensemble de l'entraînement et utilisé comme valeur statique. Skiba recommande d'utiliser une valeur statique pour D CP . P (t) est la puissance produite au temps t .
Le mathématicien Dave Waterworth (3) a aidé le développeur principal de Golden Cheetah, Mark Liversedge, à développer une optimisation de l'algorithme de skiba (6). Cette reformulation se rapproche de l'algorithme de skiba, les résultats peuvent donc varier un peu dans les cas extrêmes uniquement, en particulier lorsque ( Tau ) est très faible par rapport au temps d'échantillonnage. La partie intégrale de Bal des équations de Skiba est réécrite par Waterworth à: 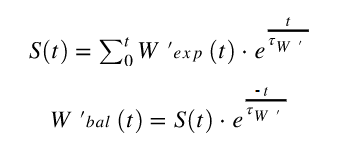
Lorsque S (T) est une somme en cours d'exécution au temps T après le début, d'autres symboles confortent les équations précédentes. Tau (ʈ W ' ) et W' exp (t) sont calculés avec les équations originales présentées par Skiba. L'algorithme de skiba intégral est assez coûteux à calculer, même sur les ordinateurs rapides, car la sommation doit être répétée pour chaque fois t à nouveau. Le gros avantage de l'optimisation de Waterworth est que le équilibre ne peut désormais être calculé en temps réel: pendant la balade et pas seulement après! De plus, il est très utile lorsque l'on veut déterminer la puissance critique à la volée lors des séances d'entraînement HIIT ou des entraînements intenses lorsque l'équilibre de W ' devient négatif et a été épuisé!
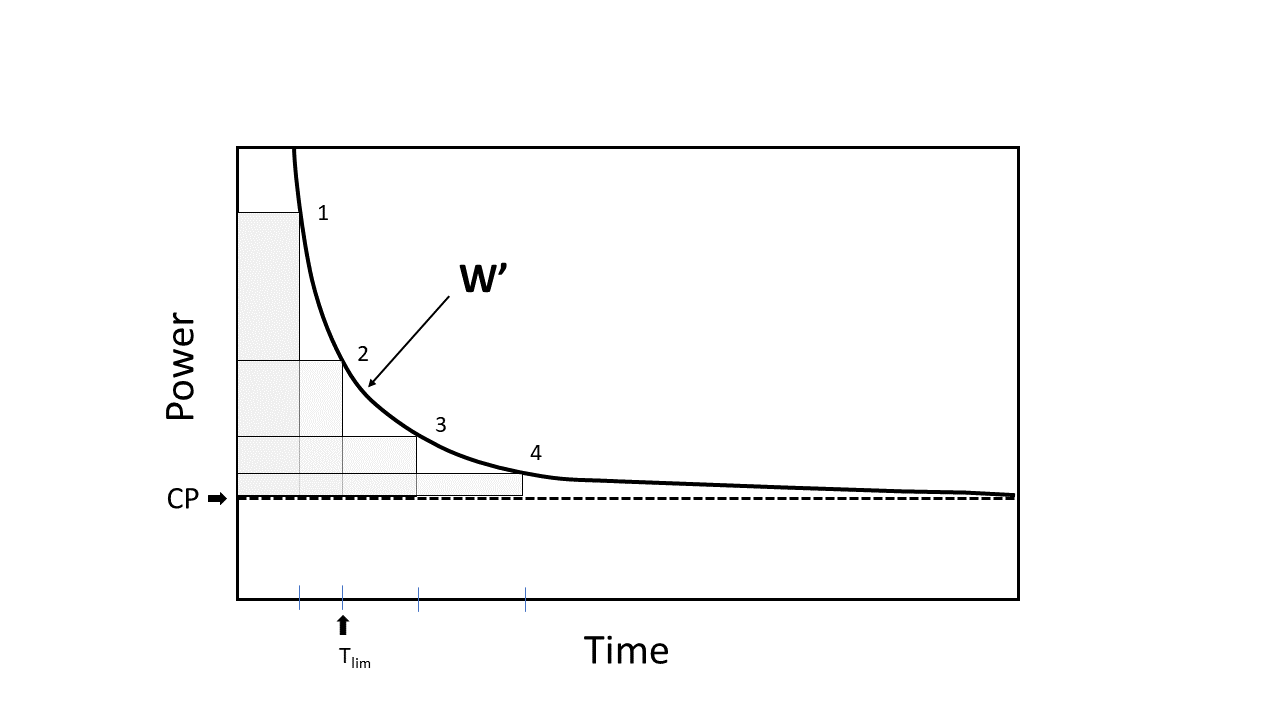
Mathématiquement, la relation de durée de puissance est décrite comme une fonction hyperbolique. Les 4 points différents sur la courbe représentent des points dans le temps ( T LIM ) lorsque la puissance durable maximale correspondante au-dessus du CP est atteinte et l'épuisement se produit. Lorsque la tolérance à l'exercice est prise en compte, l'asymptote de puissance est connue sous le nom de CP (Watts). La constante de courbure est connue sous le nom de w ' (c'est-à-dire W' prime ), elle est mesurée en unités de travail effectuées (Joules). Notez que les 4 zones grisées, représentant W ' , sont de forme différente mais à peu près de taille égale. Cette relation de durée de puissance hyperbolique peut être transformée en une relation linéaire si le travail effectué est tracé contre le temps, de sorte que la pente de la ligne équivaut à CP et que l'interception est égale à W ' . Il convient de souligner que la relation de durée de puissance décrit la tolérance de l'exercice mais ne l'explique pas. Néanmoins, les réponses physiologiques à l'exercice effectuées en dessous et au-dessus du CP peuvent fournir des informations importantes sur le processus de fatigue. Le CP a été initialement défini comme la puissance externe qui pouvait être soutenue «indéfiniment» ou pendant très longtemps sans fatigue. Cette définition doit cependant être considérée comme théorique, car aucun exercice ne peut jamais être entrepris indéfiniment. Il est maintenant entendu que CP sépare les sorties de puissance pour lesquelles la tolérance à l'exercice est prévisible limitée (puissance d'exercice> CP ). Le temps réel d'intolérance ( T LIM ) pour l'exercice effectué au-dessus du CP est défini, et donc étroitement prédit par l'équation:
T lim = w ′ / (p-cp)
Cette équation souligne que le temps d'intolérance au-dessus du CP est fonction de la proximité de la puissance de sortie ( P ) soutenue en CP et de la taille de W ' . Lorsque P est considérablement supérieur au CP , la quantité constante de travaux représentée par le paramètre W ' sera utilisée rapidement et T lim sera courte. Si P est plus proche de CP , alors « serait« utilisé »plus lentement et t lim serait plus long. Une considération cruciale ici est que W ' est supposé constant pour tout P au-dessus du CP . Ce modèle de temps de puissance ou de durée de puissance « deux paramètres » implique donc que les performances absolues de l'exercice dépend simplement de la valeur de CP (dans Watts) et de la valeur de W ' (en joules). Les paramètres CP et W ' peuvent varier considérablement selon les individus en fonction de la santé / de la maladie, de l'âge, de la forme physique et de l'entraînement.
// ------------ W' Balance calculation -------------------
// Global variables related to Cycling Power and W-Prime
uint16_t TAWC_Mode = 1 ; // Track Anaerobic Capacity Depletion Mode == TRUE -> APPLY and SHOW
uint16_t CP60 = 160 ; // Your (estimate of) Critical Power, more or less the same as FTP
uint16_t eCP = CP60; // Algorithmic estimate of Critical Power during intense workout
uint16_t w_prime_usr = 7500 ; // Your (estimate of) W-prime or a base value
uint16_t ew_prime_mod = w_prime_usr; // First order estimate of W-prime modified during intense workout
uint16_t ew_prime_test = w_prime_usr; // 20-min-test algorithmic estimate (20 minute @ 5% above eCP) of W-prime for a given eCP!
long int w_prime_balance = 0 ; // Can be negative !!!
bool IsShowWprimeValuesDominant = false ; // Boolean that determines to show W Prime data on Oled or not
// ------------------------------------------------------- // ------------------------ W'Balance Functions -----------------------------------
uint16_t CalculateAveragePowerBelowCP ( uint16_t iPower, uint16_t iCP);
void CalculateAveragePowerAboveCP ( uint16_t iPower, uint16_t &iavPwr, unsigned long &iCpACp);
double tau_w_prime_balance ( uint16_t iPower, uint16_t iCP);
void w_prime_balance_waterworth ( uint16_t iPower, uint16_t iCP, uint16_t iw_prime);
void ConstrainW_PrimeValue ( uint16_t &iCP, uint16_t &iw_prime);
uint16_t GetCPfromTwoParameterAlgorithm ( uint16_t iav_Power, unsigned long iT_lim, uint16_t iw_prime);
uint16_t GetWPrimefromTwoParameterAlgorithm ( uint16_t iav_Power, double iT_lim, uint16_t iCP);
// ------------------------ W'Balance Functions ------------------------------------ uint16_t CalculateAveragePowerBelowCP ( uint16_t iPower, uint16_t iCP){
// calculate avg_power_below_cp real time using a running sum and counter
static unsigned long int CountPowerBelowCP = 0 ;
static unsigned long int SumPowerBelowCP = 0 ;
if (iPower < iCP) {
SumPowerBelowCP += ( unsigned long int )iPower;
CountPowerBelowCP++;
}
return uint16_t (SumPowerBelowCP/CountPowerBelowCP); // average power below CP
} // end calculate avg_power_below_cp
void CalculateAveragePowerAboveCP ( uint16_t iPower, uint16_t &iavPwr, unsigned long int &iCpACp){
// calculate avg_power_above_cp real time using a running sum and counter
// returning the values by C++ reference!
static unsigned long int SumPowerAboveCP = 0 ;
SumPowerAboveCP += ( unsigned long int )iPower;
iCpACp++;
iavPwr = uint16_t (SumPowerAboveCP/iCpACp); // average power above CP
} // end calculate avg_power_above_cp
double tau_w_prime_balance ( uint16_t iPower, uint16_t iCP){
uint16_t avg_power_below_cp = CalculateAveragePowerBelowCP (iPower, iCP);
double delta_cp = double (iCP - avg_power_below_cp);
return ( double ( 546.00 ) * exp (- 0.01 * delta_cp) + double ( 316.00 ));
} // end Tau W Prime Balance
void w_prime_balance_waterworth ( uint16_t iPower, uint16_t iCP, uint16_t iw_prime) {
// Most power meters measure power, torque a.o. in a high frequency (20-60 Hz) but
// transmit (BLE) datasets to a monitoring device in much lower frequency: 1-4 times per second.
int power_above_cp = 0 ; // Power > CP
static double T_lim = 0 ; // Time (duration) while Power is above CP, the summed value of every sample time value P > CP
double w_prime_expended = 0.0 ; // Expended energy in Joules
double ExpTerm1 = 0.0 , ExpTerm2 = 0.0 ;
static double TimeSpent = 0.0 ; // Total Time spent in the workout, the summed value of every sample time value
static double running_sum = 0.0 ;
static unsigned long int CountPowerAboveCP = 0 ; // Count the Power readings above CP
static uint16_t avPower = 0 ; // Average power above CP
const long int NextLevelStep = 1000 ; // Stepsize of the next level of w-prime modification --> 1000 Joules step
static long int NextUpdateLevel = 0 ; // The next level at which to update eCP, e_w_prime_mod and ew_prime_test
// Quarq Dfour Zero Spider power meter sends between 2 and 1.2 power readings per second, dependent of POWER level !!!
// We assume that the sample frequency (number of samples per second) is VARIABLE !!!
// Determine the individual sample time in seconds, it may/will vary during the workout !!!
static unsigned long PrevReadingTime = 0 ;
double SampleTime = double ( millis ()-PrevReadingTime)/ 1000 ; // Time or duration since the previous sample, convert from millis to seconds
PrevReadingTime = millis (); // Update for the next sample
double tau = tau_w_prime_balance (iPower, iCP); // Determine the value for tau
TimeSpent += SampleTime ; // The summed value of all sample time values during the workout
power_above_cp = (iPower - iCP);
# ifdef DEBUGAIR
Serial. printf ( " Time:%6.1f ST: %4.2f tau: %f " , TimeSpent, SampleTime , tau);
# endif
// w_prime is energy and measured in Joules = Watt*second
// Determine the expended energy above CP since the previous measurement (--> i.e. during sample time)
w_prime_expended = double ( max ( 0 , power_above_cp))*SampleTime; // Determine (Watts_above_CP) * (its duration in seconds) = expended energy in Joules!
// Calculate some terms of the equation
ExpTerm1 = exp (TimeSpent/tau); // Exponential term1
ExpTerm2 = exp (-TimeSpent/tau); // Exponential term2
# ifdef DEBUGAIR
Serial. printf ( " W prime expended: %3.0f exp-term1: %f exp-term2: %f " , w_prime_expended , ExpTerm1, ExpTerm2);
# endif
running_sum = running_sum + (w_prime_expended*ExpTerm1); // Determine the running sum
# ifdef DEBUGAIR
Serial. printf ( " Running Sum: %f " , running_sum);
# endif
w_prime_balance = ( long int )( ( double )iw_prime - (running_sum*ExpTerm2) ) ; // Determine w prime balance and cast from double to int
# ifdef DEBUGAIR
Serial. printf ( " w_prime_balance: %d " , w_prime_balance);
# endif
// --------------- extra --------------------------------------------------------------------------------------
// Workout starts at a certain W'= ##,### Joules and CP = ### watts, set by the user; the algorithm increases CP and W' stepwise
// to more realistic values every time when W'balance is depleted to a certain level; -> 2-Parameter Algorithm updates CP and W'
if (power_above_cp > 0 ) {
CalculateAveragePowerAboveCP (iPower, avPower, CountPowerAboveCP); // Average power above CP is to be calculated for future use
T_lim += SampleTime ; // Time to exhaustion: the accurate sum of every second spent above CP, calculated for future use
}
# ifdef DEBUGAIR
Serial. printf ( " [%d] n " , CountPowerAboveCP);
# endif
// When working above CP, the moment comes that we need to update eCP and ew_prime !!
if ( (w_prime_balance < NextUpdateLevel) && (w_prime_expended > 0 ) ) { // W' balance is further depleted --> test for an update moment
NextUpdateLevel -= NextLevelStep; // Move down another level of depletion, update eCP, ew_prime_mod and ew_prime_test
eCP = GetCPfromTwoParameterAlgorithm (avPower, T_lim, iw_prime); // Estimate a new eCP value
ew_prime_mod = w_prime_usr - NextUpdateLevel; // Adjust ew_prime_modified to the next level of depletion to be checked
ew_prime_test = GetWPrimefromTwoParameterAlgorithm ( uint16_t (eCP* 1.045 ), double ( 1200 ), eCP); // 20-Min-test estimate for W-Prime
# ifdef DEBUGAIR
Serial. printf ( " Update of eCP - ew_prime %5d - avPower: %3d - T-lim:%6.1f --> eCP: %3d " , ew_prime_mod, avPower, T_lim, eCP);
Serial. printf ( " --> Test estimate of W-Prime: %d n " , ew_prime_test );
# endif
}
// -----------------extra -------------------------------------------------------------------------------
} // end
// Check and Set starting value of w_prime to realistic numbers!!
void ConstrainW_PrimeValue ( uint16_t &iCP, uint16_t &iw_prime) {
if (iCP < 100 ) { iCP = 100 ; } // Update to lowest level that we allow for
// First determine the "minimal" value for W_Prime according to a 20-min-test estimate, given the iCP value!
uint16_t w_prime_estimate = GetWPrimefromTwoParameterAlgorithm ( uint16_t (iCP* 1.045 ), double ( 1200 ), iCP);
if (iw_prime < w_prime_estimate) { iw_prime = w_prime_estimate; } // Update iw_prime to a realistic level
return ;
} // end
uint16_t GetCPfromTwoParameterAlgorithm ( uint16_t iav_Power, double iT_lim, uint16_t iw_prime) {
uint16_t WprimeDivTlim = uint16_t ( double (iw_prime)/iT_lim ); // type cast for correct calculations
if (iav_Power > WprimeDivTlim){ // test for out of scope
return (iav_Power - WprimeDivTlim); // Solve 2-parameter algorithm to estimate CP
} else {
return eCP; // Something went wrong do'nt allow an update of CP
}
} // end
uint16_t GetWPrimefromTwoParameterAlgorithm ( uint16_t iav_Power, double iT_lim, uint16_t iCP) {
if (iav_Power > iCP){ // test for out of scope
return (iav_Power-iCP)*(( uint16_t )iT_lim); // Solve 2-parameter algorithm to estimate new W-Prime
} else {
return w_prime_usr; // Something went wrong don't allow an update of w_prime
}
} // end
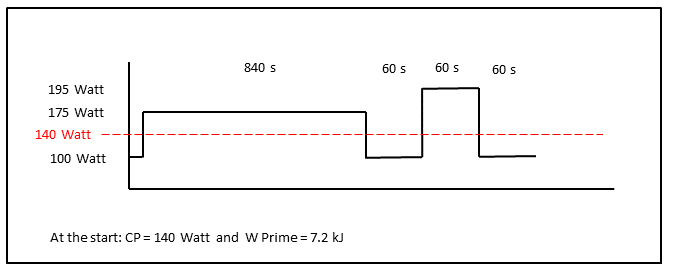
Le code a été intégré dans un projet plus grand appelé Airflow . Définir ou modifier votre CP basal et W Prime font partie intégrante d'une application compagnon de flux d'air ! Le dispositif intelligent du flux d'air d' écoute en continu la vitesse de flux d'air demandée du (s) ventilateur (s) de refroidissement pour un bilan thermique stable pendant toutes les phases d'un entraînement de cyclisme intérieur, de l'échauffement, des intervalles d'intensité, de la récupération intermittente et au chalerie. Le cycliste n'a pas d'ingérence en cours et peut pleinement se concentrer sur les exigences de l'entraînement de l'entraîneur de Stationay, toujours face à la courante aérienne idéale qui le refroidira de manière appropriée. De plus, les cyclistes obtiennent (en bonus) un aperçu du développement de sa puissance critique lorsque l'intensité de l'entraînement est intense et assez longue! Le processeur express Arduino NRF52480 appliqué est si puissant que le calcul en temps réel de CP et W PRIME peut être accompli tous les calculs pour déterminer les termes de la bilan thermique et régler les ventilateurs sur la capacité de soufflage appropriée.
Un cycliste (Propriétés: CP = 140 WATT et W PRIME = 7,2 kJ ) fait un entraînement intense avec la durée et l'intensité comme indiqué sur la figure. W prime est épuisé plusieurs fois pendant le premier bloc d'intervalle. De nouvelles valeurs pour CP et W PRIM seront estimées par l'algorithme pendant l'entraînement uniquement le cas échéant. Exécutez la vidéo pour voir une déplétion à 100% de W Prime et les valeurs estimées car elles ont été calculées en temps réel et présentées sur un écran OLED ... Remarquez comment la barre horizontale se rétrécit lorsque la puissance est au-dessus de CP à 175 et 195 watts. La barre est proportionnelle à l'équilibre de W et en outre ce qui est "laissé dans le réservoir" est indiqué en pourcentage! Les lectures sont présentées dans une séquence accélérée et ne sont pas conformes à la durée indiquée de l'entraînement!