Оптимизация колоний муравья (ACO)-это мета-гейвристическая техника в области интеллекта роя. Он используется для решения различных проблем комбинаторной оптимизации.
ACO основан на поведении муравьевой колонии и их возможности поиска для комбинаторной оптимизации. Анализ естественного поведения муравьиных колоний показывает, что муравьи движутся вдоль богатого распределения феромонов на своем пути. Алгоритм имитирует это поведение.
Проблема с продавцом (TSP) - это классическая алгоритмическая проблема, ориентированная на оптимизацию.
Лучшее решение часто означает решение, которое дешевле, короче или быстрее.
Проблема описывает продавца, который должен путешествовать между N городами, чтобы он посещает каждый город один раз во время поездки. Каждый город связан с другими городами, а ссылки имеют фиксированные веса (затраты на поездки, расстояние и т. Д.)
Набор данных состоит из 225 городов на северо-западе и центральной части индийского субконтинента.
tsp dataset/
├── distance.txt
├── location_ll.txt
├── location_map.jpg
├── location_map_satellite_image.jpg
├── names.txt
├── road_distance.txt
└── travel_time.txt
| Файл | Описание |
|---|---|
| location_ll.txt | Пространство отделяло местоположения гео (широта и долгота) каждого города. |
| Distance.txt | Евкродийское расстояние между городами. |
| Road_distance.txt | Расстояние по дороге между городами. |
| travel_time.txt | Время понадобится, чтобы поехать из одного города в другой. |
В системе Ant Colony (ACS) ряд искусственных муравьев первоначально размещаются в случайных городах. Каждый муравей строит тур (возможное решение TSP). Он выбирает следующий город, применяя правило перехода штата (жадное правило). Это правило обеспечивает баланс между исследованием новых краев и эксплуатацией накопленных знаний.
Постоянное количество феромона осаждается каждым муравей на каждом шаге на самом благоприятном маршруте (лучший тур)
Используя элитный подход, мы стараемся контролировать параметры обучения. Муравьи, которые находят лучший маршрут (качество), вознаграждаются больше, чем другие муравьи. Больше феромона наносится на лучшие маршруты, придавая значение этому конкретному туру и сокращает время для получения оптимального решения.
Количество феромона, нанесенного в зависимости от качества маршрута.
Метод Maxmin направлен на то, чтобы получить лучшее из обоих миров, близкое к оптимальному решению с быстрым временем выполнения. Это достигается путем изменения суммы к феромону, нанесенному через шаги.
Первоначально вес высок, что дает быстрый уровень обучения. Вес постепенно уменьшается до 75% завершения. Тогда модель, если она точно настроена на то, чтобы применить вес, сравнивая результаты с глобальным туром .
В конце каждого шага веса связаны в пределах максимального и мин феромонов, чтобы предотвратить сбивание решения.
Количество феромона постепенно уменьшается для первых 75% итераций. Тогда сумма зависит от качества по сравнению с лучшим туром.
params = {
'_colony_size' : "number of ants in the colony" ( default = 15 ),
'_steps' : "iteration to run through" ( default = 50 ),
'_mode' : "mode of algorithm to run the model"
} # Import model
from aco_tsp import SolveTSPUsingACO
# Setup parameters
_colony_size = 15
_steps = 50
# Select mode
# ['ACS', 'Elitist', 'MaxMin']
_mode = 'ACS'
# Nodes (latitude and longitude)
_nodes = [( 20.05961 , 77.949783 ), ( 17.075451 , 74.628664 ), ..., ( 19.4133545 , 80.0059101 )]
s
# Model setup and run
model = SolveTSPUsingACO (
mode = _mode ,
colony_size = _colony_size ,
steps = _steps ,
nodes = _nodes
)
runtime , distance = model . run () С помощью ACO мы генерируем оптимальный путь, чтобы покрыть все города, пытаясь свести к минимуму расстояние в пути. Также результат зависит от параметров алгоритма и веса краев (travel time, distance, road_distance) используемые для оптимизации пути.
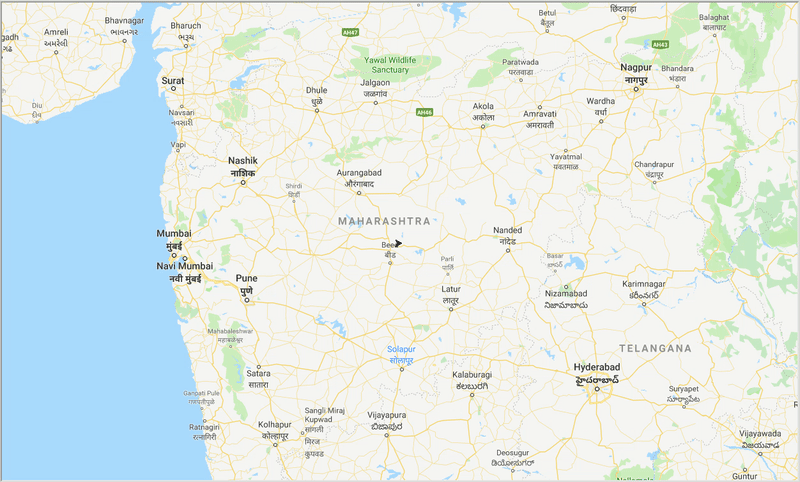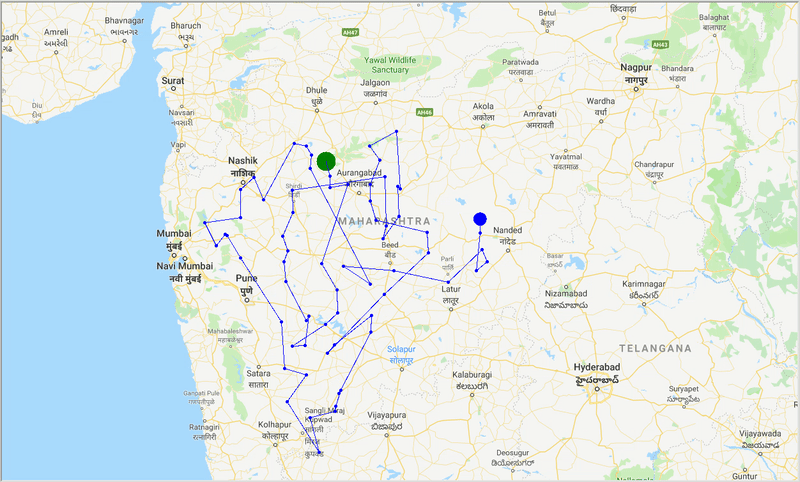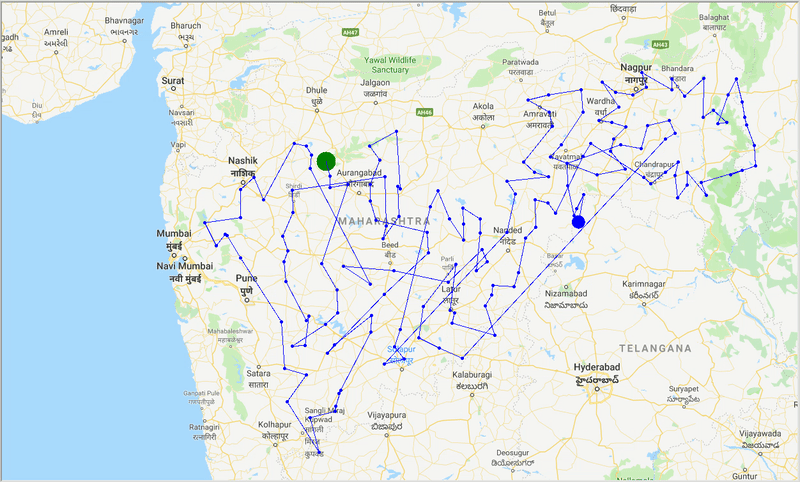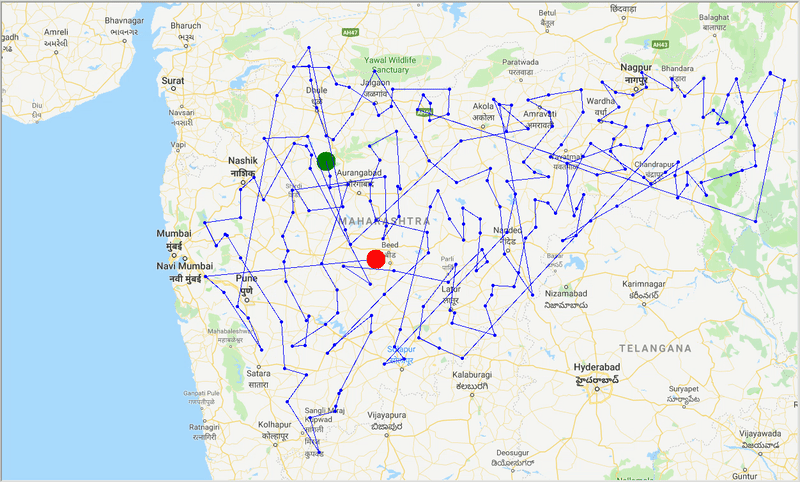
Рисунок: след оптимального пути через города