A otimização da colônia de formigas (ACO) é uma técnica meta-heurística no campo da inteligência de enxame. É usado para resolver diferentes problemas de otimização combinatória.
A ACO é baseada nos comportamentos da colônia de formigas e em sua capacidade de pesquisa para otimização combinatória. A análise do comportamento natural das colônias de formigas mostra que as formigas se movem ao longo da rica distribuição de feromônios em seu caminho. O algoritmo imita esse comportamento.
O Problema de Vendas Viajantes (TSP) é um problema algorítmico clássico focado na otimização.
Uma solução melhor geralmente significa uma solução mais barata, mais curta ou mais rápida.
O problema descreve um vendedor que deve viajar entre N cidades, de modo que ele visita cada cidade uma vez durante sua viagem. Cada cidade está conectada às outras cidades e os links têm pesos fixos (custos de viagem, distância etc.)
O conjunto de dados consiste em 225 cidades na parte noroeste e central do sub-continente indiano.
tsp dataset/
├── distance.txt
├── location_ll.txt
├── location_map.jpg
├── location_map_satellite_image.jpg
├── names.txt
├── road_distance.txt
└── travel_time.txt
| Arquivo | Descrição |
|---|---|
| location_ll.txt | Locais geográficos separados pelo espaço (latitude e longitude) de cada cidade. |
| distance.txt | Distância euclediana entre as cidades. |
| road_distance.txt | Distância por estrada entre as cidades. |
| Travel_time.txt | Tempo leve para viajar de uma cidade para outra. |
No sistema de colônia de formigas (ACS), várias formigas artificiais são inicialmente colocadas em cidades aleatórias. Cada formiga constrói um passeio (uma solução viável da TSP). Ele escolhe a próxima cidade aplicando uma regra de transição estadual (regra gananciosa). Esta regra fornece um equilíbrio entre a exploração de novas arestas e a exploração do conhecimento acumulado.
Uma quantidade constante de feromônio é depositada por cada formiga em cada etapa da rota mais favorável (melhor turnê)
Usando a abordagem elitista, tentamos controlar os parâmetros de aprendizado. As formigas que encontram a melhor rota (qualidade) são recompensadas mais do que as outras formigas. Mais feromônio é depositado em melhores rotas, dando importância a esse passeio específico e reduzindo o tempo para obter uma solução ideal.
A quantidade de feromônio depositada com base na qualidade da rota.
O método Maxmin tem como objetivo obter o melhor dos dois mundos, uma solução quase ideal com um rápido tempo de execução. Isso é conseguido variando o valor do feromônio depositado através das etapas.
Inicialmente, o peso é alto, dando uma taxa de aprendizado rápido. O peso diminui gradualmente até 75% da conclusão. Em seguida, o modelo, se for ajustado, aplicando pesos comparando os resultados com a melhor turnê global .
No final de cada etapa, os pesos são ligados dentro dos limites máximos de feromônio para impedir a solução para se desviar.
A quantidade de feromônio diminui gradualmente nos primeiros 75% das iterações. Em seguida, a quantidade depende da qualidade em comparação com a melhor turnê.
params = {
'_colony_size' : "number of ants in the colony" ( default = 15 ),
'_steps' : "iteration to run through" ( default = 50 ),
'_mode' : "mode of algorithm to run the model"
} # Import model
from aco_tsp import SolveTSPUsingACO
# Setup parameters
_colony_size = 15
_steps = 50
# Select mode
# ['ACS', 'Elitist', 'MaxMin']
_mode = 'ACS'
# Nodes (latitude and longitude)
_nodes = [( 20.05961 , 77.949783 ), ( 17.075451 , 74.628664 ), ..., ( 19.4133545 , 80.0059101 )]
s
# Model setup and run
model = SolveTSPUsingACO (
mode = _mode ,
colony_size = _colony_size ,
steps = _steps ,
nodes = _nodes
)
runtime , distance = model . run () Com a ajuda da ACO, geramos um caminho ideal para cobrir todas as cidades enquanto tentamos minimizar a distância da viagem. Além disso, o resultado depende dos parâmetros do algoritmo e dos pesos da borda (travel time, distance, road_distance) usados para otimizar o caminho.
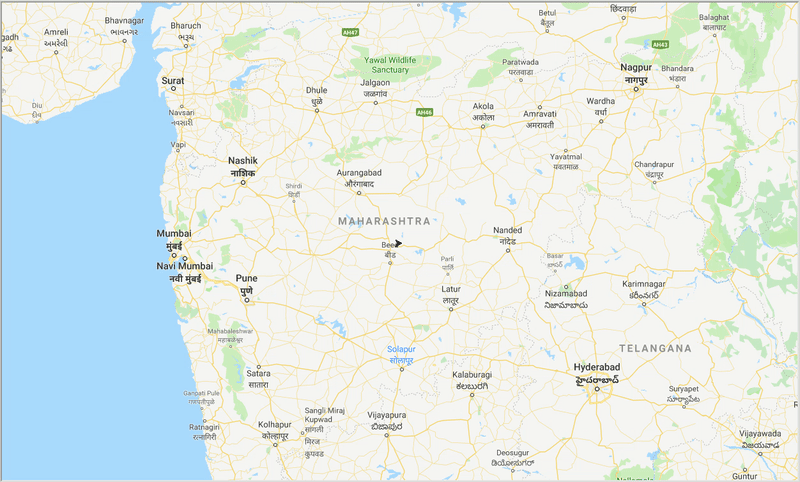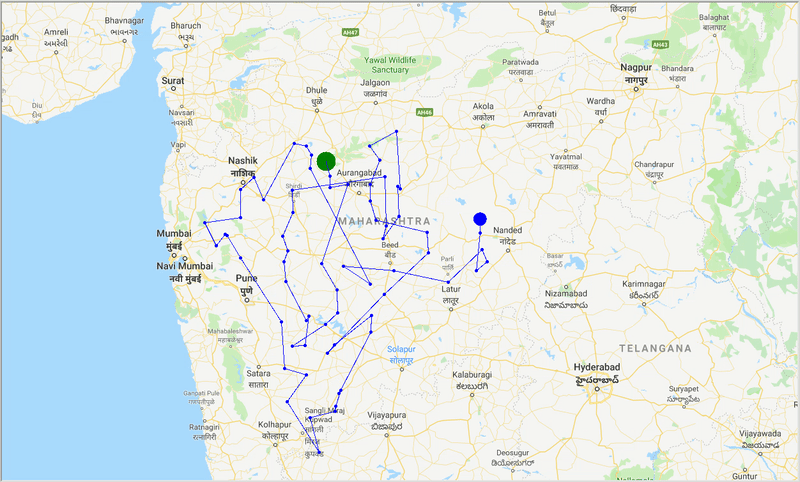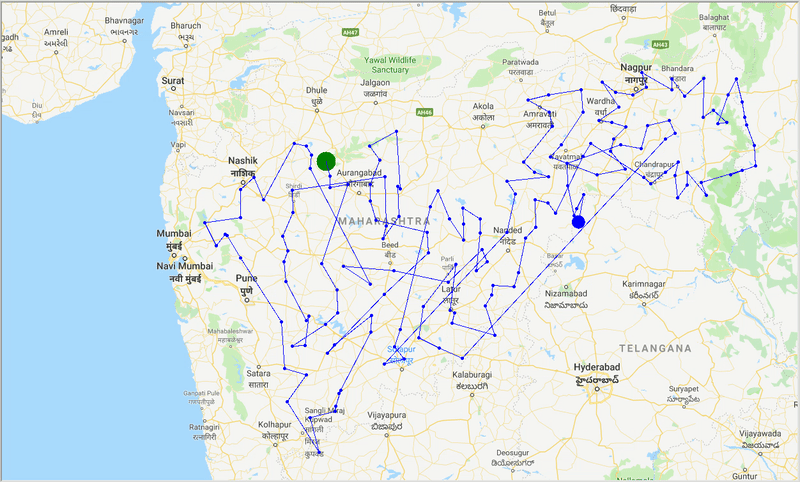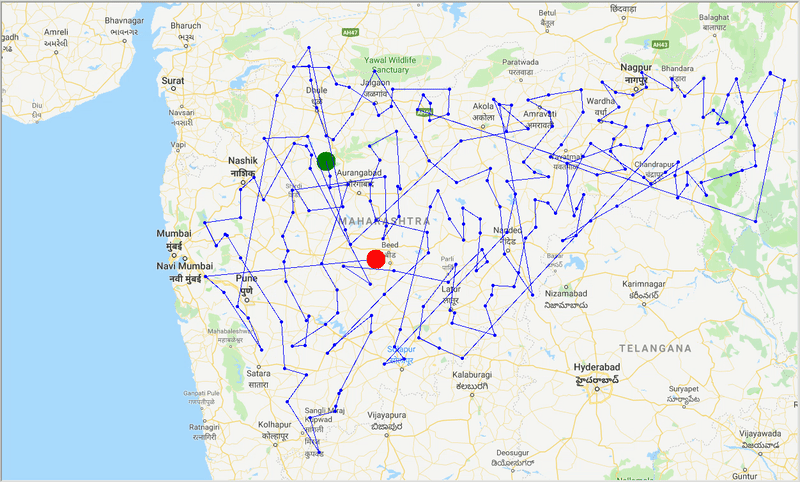
Figura: Rastreamento do caminho ideal através das cidades