L'optimisation des colonies de fourmis (ACO) est une technique méta-heuristique dans le domaine de l'intelligence de l'essaim. Il est utilisé pour résoudre différents problèmes d'optimisation combinatoire.
L'ACO est basé sur les comportements de la colonie de fourmis et leur capacité de recherche pour l'optimisation combinatoire. L'analyse du comportement naturel des colonies de fourmis montre que les fourmis se déplacent le long de la riche distribution des phéromones sur leur chemin. L'algorithme imite ce comportement.
Le problème des vendeurs itinérants (TSP) est un problème algorithmique classique axé sur l'optimisation.
Une meilleure solution signifie souvent une solution moins chère, plus courte ou plus rapide.
Le problème décrit un vendeur qui doit voyager entre les villes N de sorte qu'il visite chaque ville une fois pendant son voyage. Chaque ville est liée aux autres villes et les liens ont des poids fixes (frais de voyage, distance, etc.)
L'ensemble de données se compose de 225 villes du nord-ouest et de la partie centrale du sous-continent indien.
tsp dataset/
├── distance.txt
├── location_ll.txt
├── location_map.jpg
├── location_map_satellite_image.jpg
├── names.txt
├── road_distance.txt
└── travel_time.txt
| Déposer | Description |
|---|---|
| location_ll.txt | Les emplacements GEO séparés de l'espace (latitude et la longitude) de chaque ville. |
| distance.txt | Distance euclédienne entre les villes. |
| road_distance.txt | Distance par route entre les villes. |
| Travel_time.txt | Le temps prend pour voyager d'une ville à l'autre. |
Dans le système Ant Colony (ACS), un certain nombre de fourmis artificielles sont initialement placées dans des villes aléatoires. Chaque fourmi construit une visite (une solution réalisable du TSP). Il choisit la prochaine ville en appliquant une règle de transition de l'État (règle gourmand). Cette règle fournit un équilibre entre l'exploration des nouveaux bords et l'exploitation des connaissances accumulées.
Une quantité constante de phéromone est déposée par chaque fourmi à chaque étape de l'itinéraire le plus favorable (meilleur tour)
En utilisant l'approche élitiste, nous essayons de contrôler les paramètres d'apprentissage. Les fourmis qui trouvent le meilleur itinéraire (qualité) sont plus récompensées que les autres fourmis. Plus de phéromone est déposée sur de meilleures itinéraires, accordant de l'importance à cette tournée particulière et réduisant le temps d'obtenir une solution optimale.
La quantité de phéromone déposée en fonction de la qualité de l'itinéraire.
La méthode Maxmin vise à tirer le meilleur parti des deux mondes, une solution proche de l'optimale avec un temps d'exécution rapide. Ceci est réalisé en variant le montant à la phéromone déposée à travers les étapes.
Initialement, le poids est élevé, donnant un taux d'apprentissage rapide. Le poids diminue progressivement jusqu'à l'achèvement de 75%. Ensuite, le modèle est bien réglé en appliquant des poids en comparant les résultats à la meilleure tournée mondiale .
À la fin de chaque étape, les poids sont liés dans les limites de phéromone max et min pour empêcher la solution de s'égarer.
La quantité de phéromone diminue progressivement pour les 75% des itérations. Ensuite, le montant dépend de la qualité par rapport à la meilleure tournée.
params = {
'_colony_size' : "number of ants in the colony" ( default = 15 ),
'_steps' : "iteration to run through" ( default = 50 ),
'_mode' : "mode of algorithm to run the model"
} # Import model
from aco_tsp import SolveTSPUsingACO
# Setup parameters
_colony_size = 15
_steps = 50
# Select mode
# ['ACS', 'Elitist', 'MaxMin']
_mode = 'ACS'
# Nodes (latitude and longitude)
_nodes = [( 20.05961 , 77.949783 ), ( 17.075451 , 74.628664 ), ..., ( 19.4133545 , 80.0059101 )]
s
# Model setup and run
model = SolveTSPUsingACO (
mode = _mode ,
colony_size = _colony_size ,
steps = _steps ,
nodes = _nodes
)
runtime , distance = model . run () Avec l'aide d'ACO, nous générons un chemin optimal pour couvrir toutes les villes tout en essayant de minimiser la distance de déplacement. Le résultat dépend également des paramètres de l'algorithme et des poids des bords (travel time, distance, road_distance) utilisés pour optimiser le chemin.
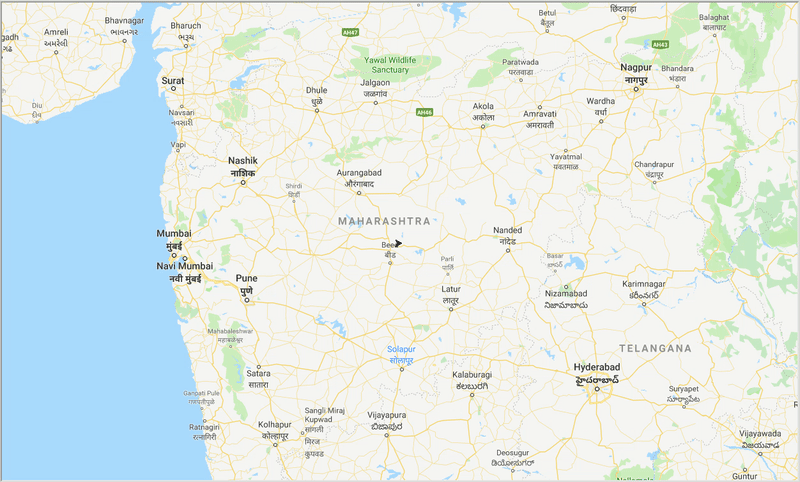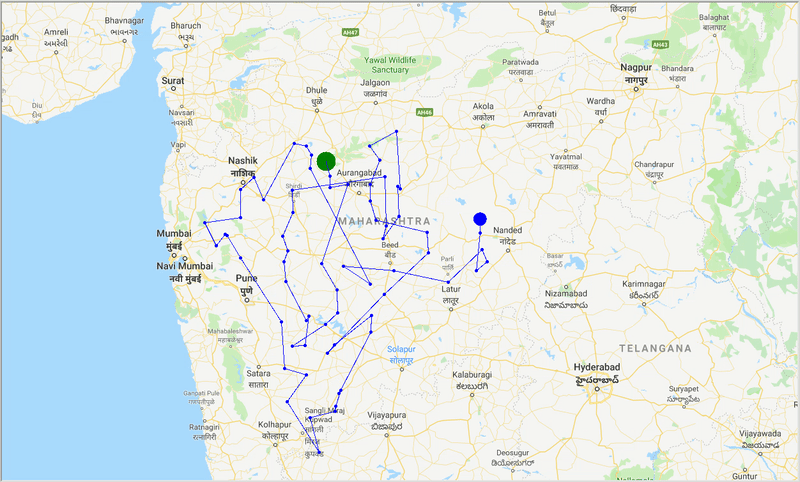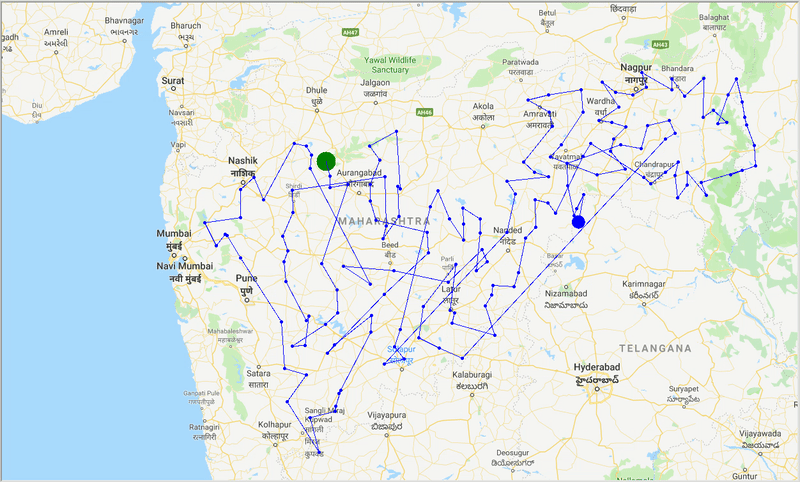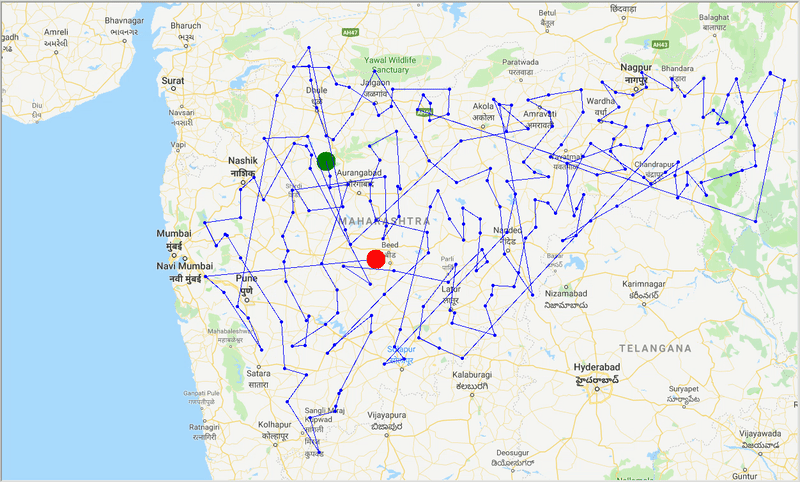
Figure: Trace d'un chemin optimal à travers les villes