TSP_ACO

Problema de vendedor ambulante utilizando la optimización de colonias de hormigas

Introducción

Optimización de colonias de hormigas

Ant Colony Optimization (ACO) es una técnica metaheurística en el campo de la inteligencia del enjambre. Se usa para resolver diferentes problemas de optimización combinatoria.

ACO se basa en los comportamientos de la colonia de hormigas y su capacidad de búsqueda para la optimización combinatoria. El análisis del comportamiento natural de las colonias de hormigas muestra que las hormigas se mueven a lo largo de la rica distribución de feromonas en su camino. El algoritmo imita este comportamiento.

Problema de vendedor ambulante

El problema de los vendedores ambulantes (TSP) es un problema algorítmico clásico centrado en la optimización.

Una mejor solución a menudo significa una solución más barata, más corta o más rápida.

El problema describe a un vendedor que debe viajar entre N ciudades de manera que visite cada ciudad una vez durante su viaje. Cada ciudad está conectada a las otras ciudades y los enlaces tienen pesos fijos (costos de viaje, distancia, etc.)

Conjunto de datos

El conjunto de datos consta de 225 ciudades en el noroeste y central del subtinente indio.

Estructura del conjunto de datos

 tsp dataset/
    ├── distance.txt
    ├── location_ll.txt
    ├── location_map.jpg
    ├── location_map_satellite_image.jpg
    ├── names.txt
    ├── road_distance.txt
    └── travel_time.txt

Descripción del archivo

Archivo	Descripción
ubicación_ll.txt	Las ubicaciones geográficas separadas en el espacio (latitud y longitud) de cada ciudad.
distancia.txt	Distancia euclediana entre las ciudades.
Road_distance.txt	Distancia por carretera entre las ciudades.
Travel_time.txt	El tiempo lleva viajar de una ciudad a otra.

Algoritmos

Sistema de colonias de hormigas

En el sistema de colonias de hormigas (ACS), una serie de hormigas artificiales se colocan inicialmente en ciudades aleatorias. Cada hormiga construye un recorrido (una solución factible del TSP). Elige la próxima ciudad aplicando una regla de transición estatal (regla codiciosa). Esta regla proporciona un equilibrio entre la exploración de nuevos bordes y la explotación del conocimiento acumulado.

Cada hormiga deposita una cantidad constante de feromona en cada paso de la ruta más favorable (mejor recorrido)

Elitista

Usando el enfoque elitista, intentamos controlar los parámetros de aprendizaje. Las hormigas que encuentran la mejor ruta (calidad) se recompensan más que las otras hormigas. Se deposita más feromona en mejores rutas, dando importancia a ese recorrido en particular y reduciendo el tiempo para obtener una solución óptima.

La cantidad de feromona depositada en función de la calidad de la ruta.

Maxmin

El método Maxmin tiene como objetivo obtener lo mejor de ambos mundos, una solución cercana a óptima con un tiempo de ejecución rápido. Esto se logra variando la cantidad a la feromona depositada a través de los pasos.

Inicialmente, el peso es alto, dando una tasa de aprendizaje rápida. El peso disminuye gradualmente hasta el 75% de finalización. Luego, el modelo si se ajusta fino aplicando pesos comparando los resultados con la mejor gira global .

Al final de cada paso, los pesos están unidos dentro de los límites de feromonas MAX y MIN para evitar que la solución se extraviera.

La cantidad de feromona disminuye gradualmente para el primer 75% de las iteraciones. Entonces la cantidad depende de la calidad en comparación con la mejor gira.

Parámetros

 params = {
    '_colony_size' : "number of ants in the colony"  ( default = 15 ),
    '_steps' : "iteration to run through" ( default = 50 ),
    '_mode' : "mode of algorithm to run the model"
}

Uso

 # Import model
from aco_tsp import SolveTSPUsingACO

# Setup parameters
_colony_size = 15
_steps = 50

# Select mode
# ['ACS', 'Elitist', 'MaxMin']
_mode = 'ACS'

# Nodes (latitude and longitude)
_nodes = [( 20.05961 , 77.949783 ), ( 17.075451 , 74.628664 ), ..., ( 19.4133545 , 80.0059101 )]
s
# Model setup and run
model = SolveTSPUsingACO (
    mode = _mode ,
    colony_size = _colony_size ,
    steps = _steps ,
    nodes = _nodes
)

runtime , distance = model . run ()

Resultado

Con la ayuda de ACO, generamos un camino óptimo para cubrir todas las ciudades mientras intentamos minimizar la distancia de viaje. También el resultado depende de los parámetros del algoritmo y los pesos de borde (travel time, distance, road_distance) utilizados para optimizar la ruta.

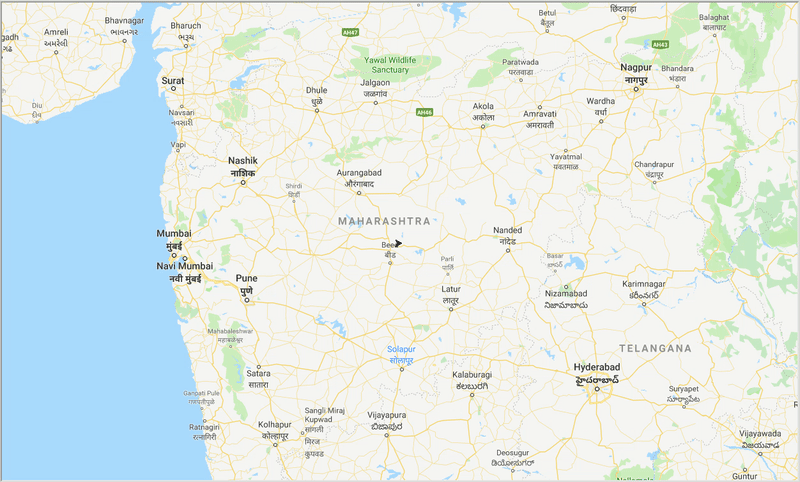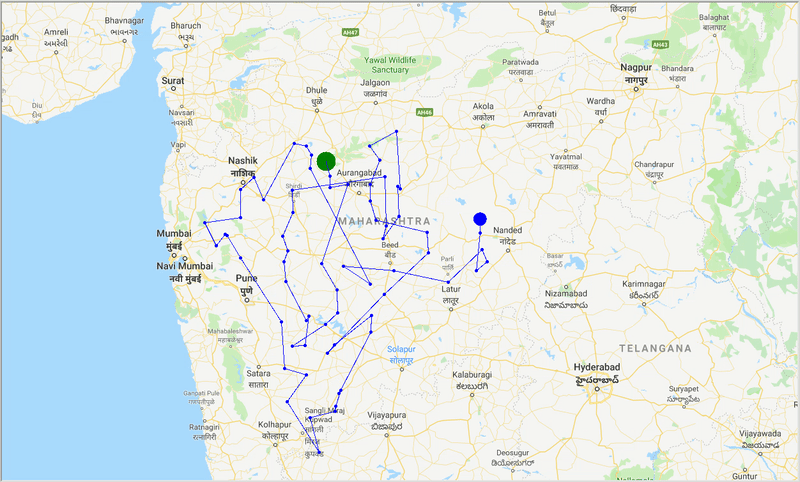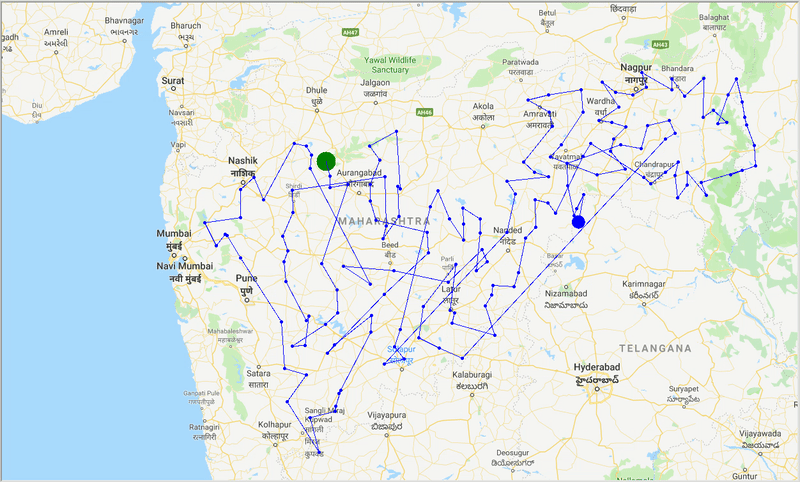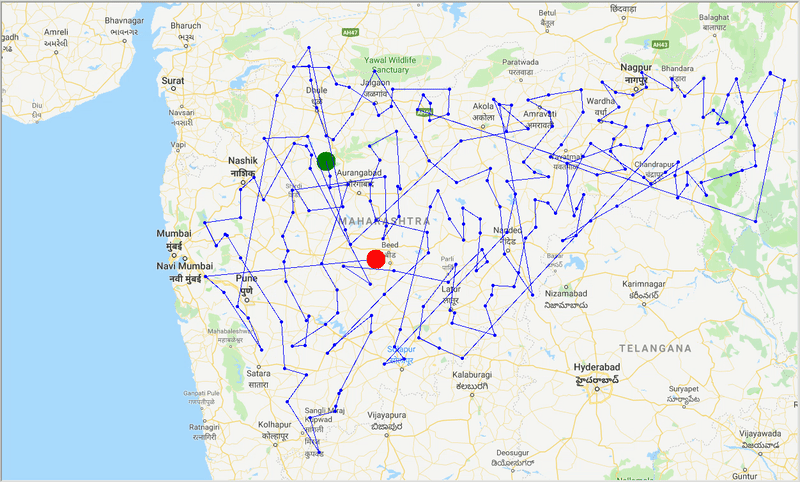
Figura: traza de ruta óptima a través de las ciudades