TSP_ACO

Problem mit der Optimierung des reisenden Verkäufers mit der Ameisenkolonie -Optimierung

Einführung

Ameisenkolonieoptimierung

Ameisenkolonieoptimierung (ACO) ist eine meta-heuristische Technik auf dem Gebiet der Schwarminformation. Es wird zur Lösung verschiedener kombinatorischer Optimierungsprobleme verwendet.

ACO basiert auf dem Verhalten der Ameisenkolonie und ihrer Suchfunktion für die kombinatorische Optimierung. Die Analyse des natürlichen Verhaltens von Ameisenkolonien zeigt, dass sich die Ameisen entlang der reichen Pheromonverteilung auf ihrem Weg bewegen. Der Algorithmus imitiert dieses Verhalten.

Problem mit reisenden Verkäufern

Das Travel Salesman -Problem (TSP) ist ein klassisches algorithmisches Problem, das sich auf die Optimierung konzentriert.

Eine bessere Lösung bedeutet oft eine Lösung, die billiger, kürzer oder schneller ist.

Das Problem beschreibt einen Verkäufer, der zwischen N -Städten reisen muss, so dass er während seiner Reise jede Stadt einmal besucht. Jede Stadt ist mit den anderen Städten verbunden und die Verbindungen haben feste Gewichte (Reisekosten, Entfernung usw.)

Datensatz

Der Datensatz besteht aus 225 Städten im nordwestlichen und zentralen Teil des indischen Unterkontinents.

Datensatzstruktur

 tsp dataset/
    ├── distance.txt
    ├── location_ll.txt
    ├── location_map.jpg
    ├── location_map_satellite_image.jpg
    ├── names.txt
    ├── road_distance.txt
    └── travel_time.txt

Dateibeschreibung

Datei	Beschreibung
location_ll.txt	Der Raum trennte die Geo -Standorte (Breitengrad und Länge) jeder Stadt.
Distanz.txt	Eucledian Distanz zwischen den Städten.
road_distance.txt	Entfernung auf der Straße zwischen den Städten.
Travel_time.txt	Es dauert die Zeit, von einer Stadt in eine andere zu reisen.

Algorithmen

Ameisenkoloniensystem

Im Ameisenkoloniensystem (ACS) werden zunächst eine Reihe künstlicher Ameisen in zufälligen Städten platziert. Jede Ameise baut eine Tour (eine praktikable Lösung des TSP). Es wählt die nächste Stadt durch die Anwendung einer staatlichen Übergangsregel (gierige Regel). Diese Regel bietet ein Gleichgewicht zwischen der Erforschung neuer Kanten und der Ausbeutung des akkumulierten Wissens.

Eine konstante Menge an Pheromon wird von jeder Ameise auf jedem Schritt auf der günstigsten Route (Best Tour) abgelagert

Elitär

Mit dem elitären Ansatz versuchen wir, die Lernparameter zu steuern. Die Ameisen, die die beste Route (Qualität) finden, werden mehr belohnt als die anderen Ameisen. Mehr Pheromon wird auf besseren Routen hinterlegt, wodurch diese bestimmte Tour wichtig ist und die Zeit für eine optimale Lösung verringert wird.

Die Menge an Pheromon, die auf der Grundlage der Qualität der Route hinterlegt ist.

Maxmin

Die Maxmin -Methode zielt darauf ab, das Beste aus beiden Welten zu erhalten, eine nahezu optimale Lösung mit einer schnellen Ausführungszeit. Dies wird erreicht, indem der Betrag zu Pheromon variiert, das durch die Schritte abgelagert wurde.

Zunächst ist das Gewicht hoch und ergibt eine schnelle Lernrate. Das Gewicht nimmt allmählich bis zu 75% ab. Dann das Modell, wenn Fein durch Anwenden von Gewichten durch Vergleich der Ergebnisse mit der globalen besten Tour vergleicht wird.

Am Ende jedes Schritts sind die Gewichte innerhalb der Max- und Min -Pheromongrenzen gebunden, um zu verhindern, dass die Lösung für das Laufen in die Irre ist.

Die Menge an Pheromon nimmt bei den ersten 75% der Iterationen allmählich ab. Dann hängt die Menge von der Qualität im Vergleich zur besten Tour ab.

Parameter

 params = {
    '_colony_size' : "number of ants in the colony"  ( default = 15 ),
    '_steps' : "iteration to run through" ( default = 50 ),
    '_mode' : "mode of algorithm to run the model"
}

Verwendung

 # Import model
from aco_tsp import SolveTSPUsingACO

# Setup parameters
_colony_size = 15
_steps = 50

# Select mode
# ['ACS', 'Elitist', 'MaxMin']
_mode = 'ACS'

# Nodes (latitude and longitude)
_nodes = [( 20.05961 , 77.949783 ), ( 17.075451 , 74.628664 ), ..., ( 19.4133545 , 80.0059101 )]
s
# Model setup and run
model = SolveTSPUsingACO (
    mode = _mode ,
    colony_size = _colony_size ,
    steps = _steps ,
    nodes = _nodes
)

runtime , distance = model . run ()

Ergebnis

Mit Hilfe von ACO erzeugen wir einen optimalen Weg, um alle Städte abzudecken, während wir versuchen, die Reisedistanz zu minimieren. Auch das Ergebnis hängt von den Parametern des Algorithmus und den Kantengewichten (travel time, distance, road_distance) ab, die zur Optimierung des Pfades verwendet werden.

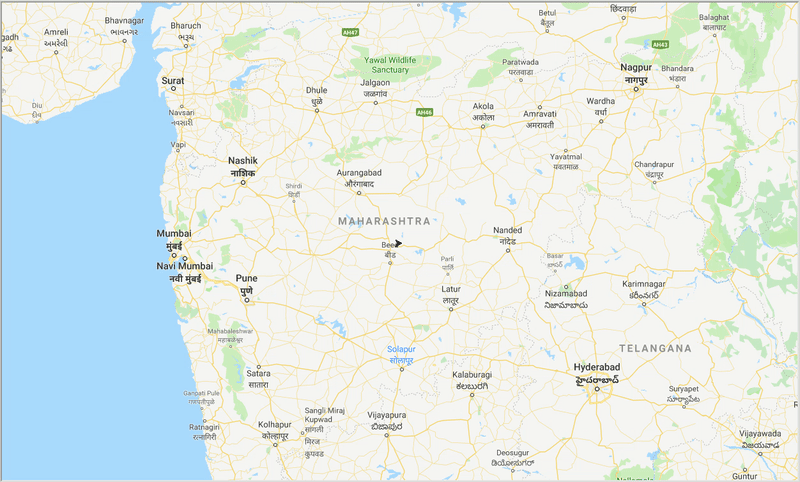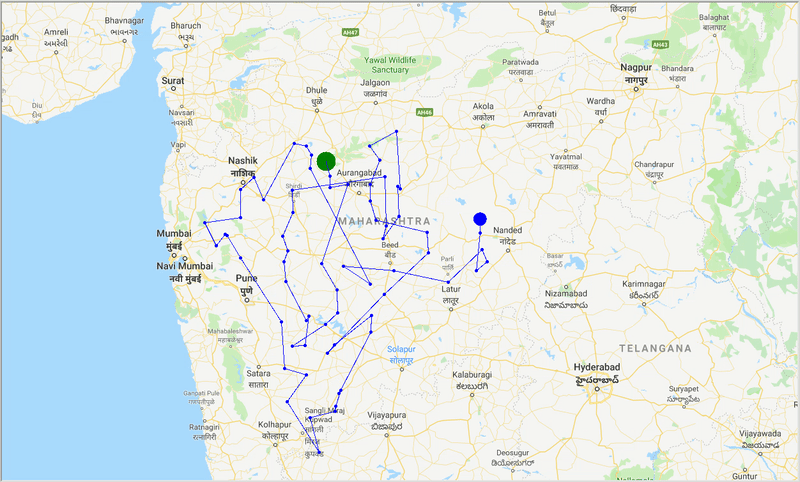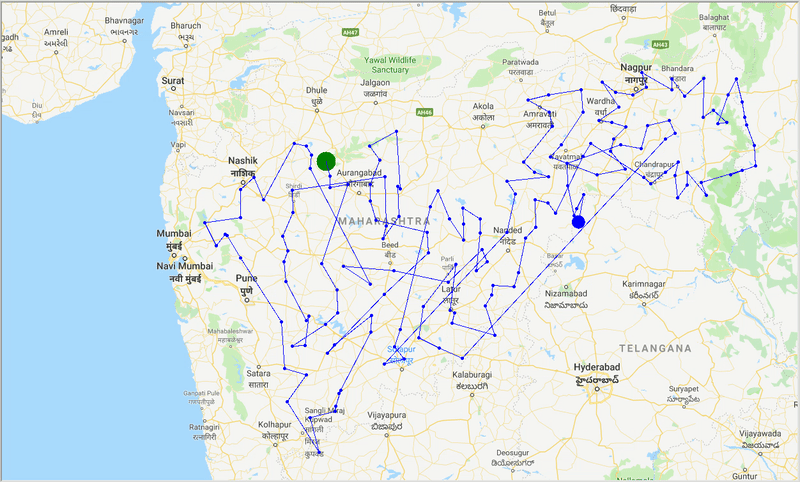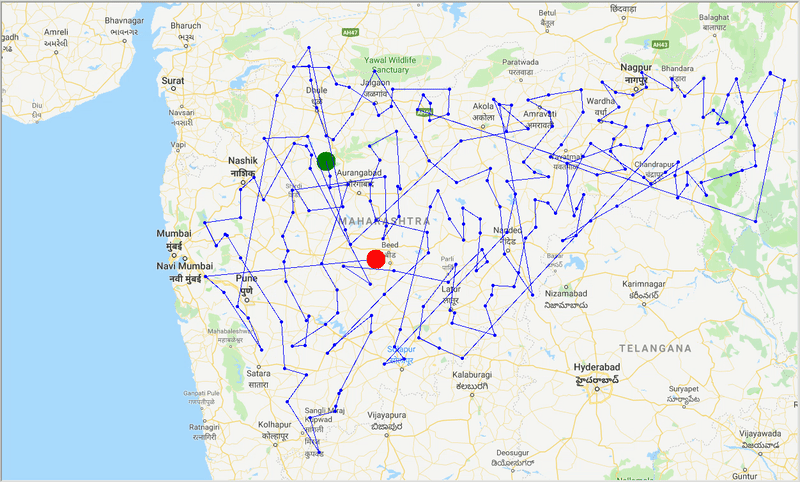
Abbildung: Spur eines optimalen Pfades durch die Städte