proxsuite

Proxsuite est une collection de solveurs numériques numériques, numériquement robustes, précis et efficaces (par exemple, LPS, QPS, etc.) enracinés dans des algorithmes proximaux primaux révisés. Grâce à ProxSuite , nous visons à offrir aux optimistes des évolutions de la communauté qui traitent des problèmes denses, clairsemés ou sans matrice. Bien que la première application ciblée soit la robotique, ProxSuite peut être utilisée dans d'autres contextes sans limites.

Proxsuite est activement développée et soutenue par les groupes de recherche Willow et Sierra, des équipes de recherche conjointes entre INRIA, École Normale Supérieure de Paris et Centre National de la Recherche Scientifique localisé en France.

Proxsuite est déjà intégrée à:

• Langue de modélisation CVXPY pour les problèmes d'optimisation convexe,
• Cadre symbolique de Casadi pour l'optimisation numérique dans le contrôle général et optimal. ProxQP est disponible à Casadi en tant que plugin pour résoudre les programmes quadratiques,
• TSID: logiciel robotique pour une dynamique inverse du robot efficace avec des contacts et basée sur Pinocchio.

Nous sommes prêts à intégrer ProxSuite dans d'autres écosystèmes d'optimisation.

Fonctionnalités principales proxsuites

Proxsuite est rapide:

• Bibliothèque de modèles C ++,
• adapté au cache.

ProxSuite est polyvalente, offrant à travers une API unifiée des algorithmes avancés spécialisés pour exploiter efficacement les structures de problèmes:

• Backends de factorisation de matrice dense, clairsemés et sans matrice,
• Options avancées de démarrage à chaud (par exemple, options initiales de supposition initiale à base d'égalité, de démarrage chaud ou de démarrage à froid à partir des résultats précédents),

avec des fonctionnalités dédiées pour

• Gestion des contraintes de boîtes plus efficaces, des programmes linéaires, du QP avec de la hesse diagonale ou avec beaucoup plus de contraintes que les variables primaires,
• Résolution de QP non convexes,
• Résolution des lots de QPS en parallèle,
• Résolvant le QP réalisable le plus proche si le QP semble être primitif,
• différenciation des QP réalisables et irréalisables.

Proxsuite est flexible:

• en-tête seulement,
• C ++ 14/17/20 conforme,
• Les liaisons Python et Julia pour un prototypage de code facile sans sacrifier les performances.

Proxsuite est extensible. Proxsuite est fiable et très testée, montrant les meilleures performances sur les problèmes les plus difficiles de la littérature. ProxSuite est prise en charge et testée sur Windows, Mac OS X, Unix et Linux.

Documentation

La documentation de proxsuite en ligne de la dernière version est disponible ici.

Commencer

Proxsuite est distribuée à de nombreux gestionnaires de packages bien connus.

Installation rapide avec:

   pip install proxsuite

Cette approche est disponible sur Linux, Windows et Mac OS X.

Installation rapide avec:

   conda install proxsuite -c conda-forge

Cette approche est disponible sur Linux, Windows et Mac OS X.

Installation rapide avec:

   brew install proxsuite

Cette approche est disponible sur Linux et Mac OS X.

Approches alternatives

L'installation de la source est présentée ici.

Compilation d'un premier exemple de programme

Pour les performances les plus rapides, utilisez la commande suivante pour activer la vectorisation lors de la compilation de l'exemple simple.

g++ -O3 -march=native -DNDEBUG -std=gnu++17 -DPROXSUITE_VECTORIZE examples/first_example_dense.cpp -o first_example_dense $( pkg-config --cflags proxsuite )

Utilisation de proxsuite avec CMake

Si vous souhaitez utiliser ProxSuite avec CMake, le petit exemple suivant devrait vous aider:

 cmake_minimum_required ( VERSION 3.10)

project (Example CXX)
find_package (proxsuite REQUIRED)
set (CMAKE_CXX_STANDARD 17) # set(CMAKE_CXX_STANDARD 14) will work too

add_executable (example example.cpp)
target_link_libraries (example PUBLIC proxsuite::proxsuite)

# Vectorization support via SIMDE and activated by the compilation options '-march=native' or `-mavx2 -mavx512f`
add_executable (example_with_full_vectorization_support example.cpp)
target_link_libraries (example_with_full_vectorization_support PUBLIC proxsuite::proxsuite-vectorized)
target_compile_options (example_with_full_vectorization_support PUBLIC "-march=native" )

Si vous avez compilé ProxSuite avec le support de vectorisation, vous pouvez également utiliser le CMake Target proxsuite::proxsuite-vectorized pour lier également SIMDE. N'oubliez pas d'utiliser -march=native pour obtenir les meilleures performances.

Proxqp

L'algorithme ProxQP est une approche d'optimisation numérique pour résoudre les problèmes de programmation quadratique de la forme:

$ee

où $ x in mathbb {r} ^ n $ est la variable d'optimisation. La fonction objectif est définie par une matrice de semi-fini positive $ H in mathcal {s} ^ n _ + $ et un vecteur $ g in mathbb {r} ^ n $ . Les contraintes linéaires sont définies par la matrice de contrainte d'égalité $ A in mathbb {r} ^ {n_ text {eq} Times n} $ et la matrice de contrainte des inégalités $ C in mathbb {r} ^ {n_ text {in} Times n} $ Et les vecteurs $ b in mathbb {r} ^ {n_ text {eq}} $ , $ l in mathbb {r} ^ {n_ text {in}} $ et $ u in mathbb {r} ^ {n_ text {in}} $ de sorte que $ b_i in mathbb {r}, ~ forall i = 1, ..., n_ text {eq} $ et $ l_i in mathbb {r} cup {- infty} $ et $ u_i in mathbb {r} cup {+ infty}, ~ forall i = 1, ..., n_ text {in} $ .

Citant proxqp

Si vous utilisez ProxQP pour votre travail, nous vous encourageons à citer le document connexe.

Benchmarks numériques

Les références numériques de ProxQP contre d'autres solveurs commerciaux et open source sont disponibles ici.

Pour les programmes quadratiques convexes denses avec des contraintes d'inégalité et d'égalité, lorsqu'ils demandent une précision relativement élevée (par exemple, 1E-6), on obtient les résultats suivants.

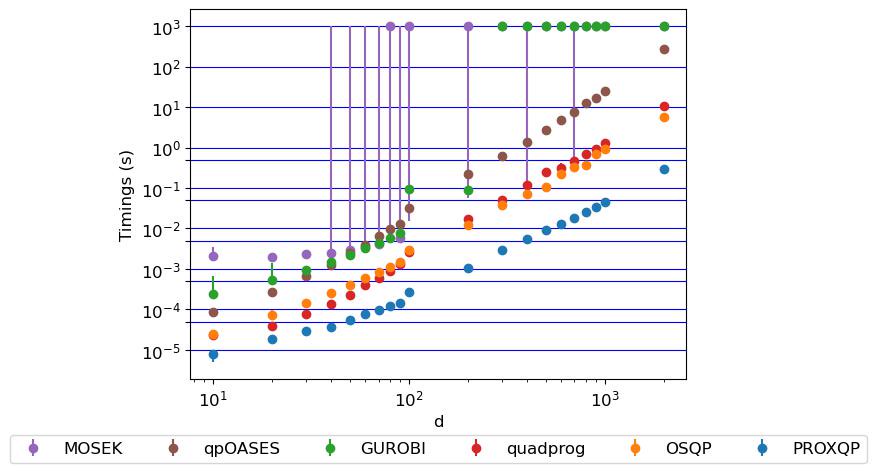
Sur l'axe des y, vous pouvez voir des horaires en secondes, et sur la dimension de l'axe X WRT à la variable primaire des problèmes quadratiques aléatoires générés (le nombre de contraintes du problème généré est la moitié de la taille de sa dimension primitive). Pour chaque dimension, le problème est généré sur différentes graines, et les horaires sont obtenus en moyennes sur des courses successives pour les mêmes problèmes. Ce graphique montre pour chaque solveur de référence et programme quadratique aléatoire généré, des calendriers de bar, y compris la médiane (comme point) et les valeurs minimales et maximales obtenues (définissant l'amplitude de la barre). Vous pouvez voir que ProxQP est toujours inférieur aux solveurs, ce qui signifie qu'il est le plus rapide pour ce test.

Pour les problèmes difficiles du test de test Maros Meszaros, lorsqu'ils demandent une précision élevée (par exemple, 1E-9), on obtient les résultats ci-dessous.

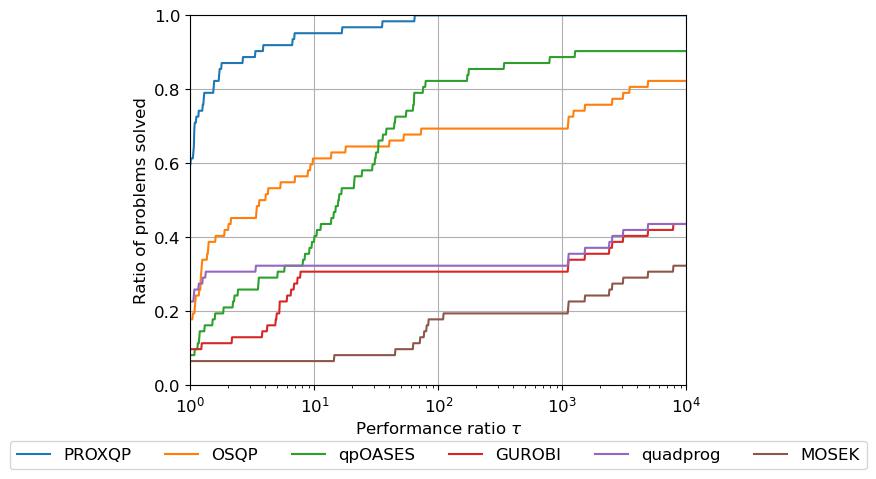
Le graphique ci-dessus rapporte les profils de performance de différents solveurs. Il est classique pour les résolveurs d'analyse comparative. Les profils de performance correspondent à la fraction des problèmes résolus (sur l'axe y) en fonction de certains temps d'exécution (sur l'axe x, mesuré en termes de multiple de l'exécution du solveur le plus rapide pour ce problème). Donc, mieux c'est, mieux c'est. Vous pouvez voir que ProxQP résout le plus rapidement plus de 60% des problèmes (c'est-à-dire pour $ tau = 1 $ ) et que pour résoudre environ 90% des problèmes, il est au plus 2 fois plus lent que les résolveurs les plus rapides résolvant ces problèmes (c'est-à-dire pour $ tau approx2 $ ).

Remarque: Tous ces résultats ont été obtenus avec un CPU Intel (R) Core (R) I7-11850H à 2,50 GHz.

Qplayer

QPlayer permet d'utiliser un QP comme couche dans des architectures d'apprentissage standard. Plus précisément, QPlayer se différencie $ theta $ les solutions primordiales et doubles de QP de la forme

$$ begin {align} min_ {x} & ~ frac {1} {2} x ^ {t} h ( theta) x + g ( theta) ^ {t} x \ text {st} & ~ a ( theta) x = b ( theta) \ & ~ l ( theta) leq c ( theta) ~ l ( theta) leq C ( theta) u ( theta) end {align} $$

où $ x in mathbb {r} ^ n $ est la variable d'optimisation. La fonction objectif est définie par une matrice de semi-fini positive $ H ( theta) in mathcal {s} ^ n _ + $ et un vecteur $ g ( theta) in mathbb {r} ^ n $ . Les contraintes linéaires sont définies par la matrice de contrainte d'égalité $ A ( theta) in mathbb {r} ^ {n_ text {eq} Times n} $ et la matrice de contrainte des inégalités $ C ( theta) in mathbb {r} ^ {n_ text {in} Times n} $ Et les vecteurs $ b in mathbb {r} ^ {n_ text {eq}} $ , $ l ( theta) in mathbb {r} ^ {n_ text {in}} $ et $ u ( theta) in mathbb {r} ^ {n_ text {in}} $ de sorte que $ b_i in mathbb {r}, ~ forall i = 1, ..., n_ text {eq} $ et $ l_i in mathbb {r} cup {- infty} $ et $ u_i in mathbb {r} cup {+ infty}, ~ forall i = 1, ..., n_ text {in} $ .

QPlayer est capable d'apprendre plus d'architectures structurées. Par exemple, $ theta $ peut consister uniquement à apprendre certains éléments de $ A $ tout en laissant $ b $ Correction (voir par exemple, l'exemple sur la façon d'inclure QPlayer dans un pipeline d'apprentissage). QPlayer peut également différencier les LP. QPlayer permet un calcul parallélisé sur des processeurs et est interfacé avec Pytorch .

Citant qplayer

Si vous utilisez QPlayer pour votre travail, nous vous encourageons à citer l'article connexe.

Procédure d'installation

Veuillez suivre la procédure d'installation ici.