proxsuite

ProxSuite es una colección de solucionadores numéricos de código abierto, numéricamente robustos, precisos y eficientes (p. Ej. A través de ProxSuite , nuestro objetivo es ofrecer a los optimizadores escalables de la comunidad que tratan con problemas densos, escasos o sin matriz. Si bien la primera aplicación dirigida es robótica, el proxsuite se puede usar en otros contextos sin límites.

Proxsuite es desarrollado y apoyado activamente por los grupos de investigación de Willow y Sierra, los equipos de investigación conjuntos entre Inria, la École Normale Supérieure de Paris y el Centro Nacional de la Cientifique del Centro Nacional de la Cientifique localizados en Francia.

ProxSuite ya está integrado en:

• Lenguaje de modelado de CVXPY para problemas de optimización convexa,
• El marco simbólico de Casadi para la optimización numérica en general y el control óptimo. ProXQP está disponible en Casadi como un complemento para resolver programas cuadráticos,
• TSID: software robótico para una dinámica inversa de robot eficiente con contactos y basado en Pinocho.

Estamos listos para integrar proxsuite dentro de otros ecosistemas de optimización.

Características principales de proxsuite

ProxSuite es rápido:

• Biblioteca de plantillas C ++,
• amigable con la caché.

ProxSuite es versátil, ofreciendo a través de un algoritmos avanzados de API unificados especializados para explotar de manera eficiente estructuras de problemas:

• Backends de factorización de matriz denso, escaso y sin matriz,
• Opciones avanzadas de arranque cálido (por ejemplo, suposiciones iniciales limitadas por igualdad, opciones de inicio cálido o de arranque en frío de resultados anteriores),

con características dedicadas para

• Manejo de restricciones de caja más eficientes, programas lineales, QP con Hessian diagonal o con muchas más restricciones que las variables primarias,
• Resolver QP no convexos,
• Resolver lotes de QPS en paralelo,
• Resolver el QP factible más cercano si el QP parece ser involuntario,
• Diferenciando QP factibles e inflables.

ProxSuite es flexible:

• solo encabezado,
• C ++ 14/17/20 Cumplante,
• Python y Julia Bindings para obtener prototipos de código fácil sin sacrificar el rendimiento.

Proxsuite es extensible. ProxSuite es confiable y ampliamente probado, mostrando los mejores rendimientos en los problemas más difíciles de la literatura. ProxSuite es compatible y probado en Windows, Mac OS X, Unix y Linux.

Documentación

La documentación proxsuite en línea de la última versión está disponible aquí.

Empezando

ProxSuite se distribuye a muchos administradores de paquetes conocidos.

Instalación rápida con:

   pip install proxsuite

Este enfoque está disponible en Linux, Windows y Mac OS X.

Instalación rápida con:

   conda install proxsuite -c conda-forge

Este enfoque está disponible en Linux, Windows y Mac OS X.

Instalación rápida con:

   brew install proxsuite

Este enfoque está disponible en Linux y Mac OS X.

Enfoques alternativos

La instalación desde la fuente se presenta aquí.

Compilación de un primer programa de ejemplo

Para el rendimiento más rápido, use el siguiente comando para habilitar la vectorización al compilar el ejemplo simple.

g++ -O3 -march=native -DNDEBUG -std=gnu++17 -DPROXSUITE_VECTORIZE examples/first_example_dense.cpp -o first_example_dense $( pkg-config --cflags proxsuite )

Usar proxsuite con cmake

Si desea usar proxsuite con cmake, el siguiente ejemplo pequeño debería ayudarlo:

 cmake_minimum_required ( VERSION 3.10)

project (Example CXX)
find_package (proxsuite REQUIRED)
set (CMAKE_CXX_STANDARD 17) # set(CMAKE_CXX_STANDARD 14) will work too

add_executable (example example.cpp)
target_link_libraries (example PUBLIC proxsuite::proxsuite)

# Vectorization support via SIMDE and activated by the compilation options '-march=native' or `-mavx2 -mavx512f`
add_executable (example_with_full_vectorization_support example.cpp)
target_link_libraries (example_with_full_vectorization_support PUBLIC proxsuite::proxsuite-vectorized)
target_compile_options (example_with_full_vectorization_support PUBLIC "-march=native" )

Si ha compilado proxSuite con el soporte de vectorización, también puede usar el objetivo CMAKE proxsuite::proxsuite-vectorized para vincular también contra SIMDE. No olvide usar -march=native para obtener el mejor rendimiento.

Proxqp

El algoritmo ProXQP es un enfoque de optimización numérica para resolver problemas de programación cuadrática de la forma:

$$ begin {align} min_ {x} & ~ frac {1} {2} x^{t} hx+g^{t} x \ text {st} & ~ a x = b \ & ~ l leq c x leq u end {align} $$

dónde $ x in mathbb {r}^n $ es la variable de optimización. La función objetivo se define por una matriz semidefinita positiva $ H in mathcal {s}^n _+$ y un vector $ g in mathbb {r}^n $ . Las restricciones lineales se definen por la matriz de contratación de igualdad $ A in mathbb {r}^{n_ text {eq} times n} $ y la matriz de restricción de desigualdad $ C in mathbb {r}^{n_ text {in} times n} $ y los vectores $ b in mathbb {r}^{n_ text {eq}} $ , $ l in mathbb {r}^{n_ text {in}} $ y $ u in mathbb {r}^{n_ text {in}} $ de modo que $ b_i in mathbb {r}, ~ forall i = 1, ..., n_ text {eq} $ y $ l_i in mathbb {r} cup { - infty} $ y $ u_i in mathbb {r} cup { + infty}, ~ forall i = 1, ..., n_ text {in} $ .

Citando proxqp

Si está utilizando ProXQP para su trabajo, le recomendamos que cite el documento relacionado.

Puntos de referencia numéricos

Aquí están disponibles los puntos de referencia numéricos de ProXQP con otros solucionadores comerciales y de código abierto.

Para los programas cuadráticos convexos densos con restricciones de desigualdad e igualdad, al solicitar una precisión relativamente alta (p. Ej., 1e-6), uno obtiene los siguientes resultados.

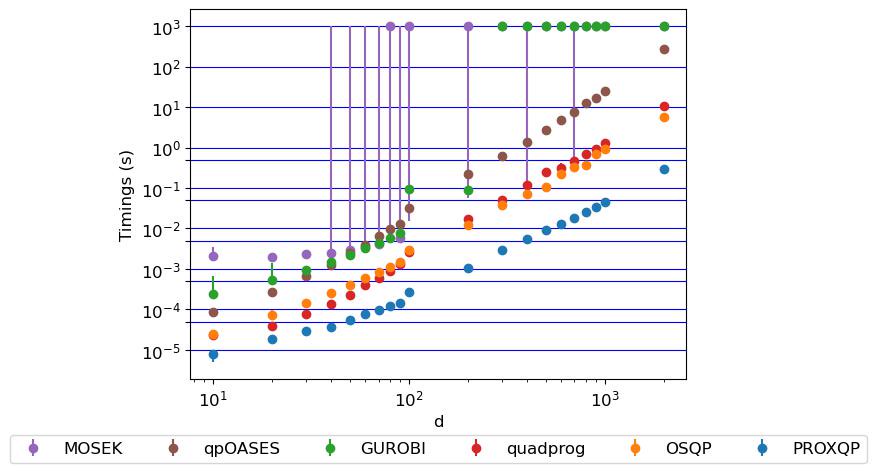
En el eje Y, puede ver los horarios en segundos, y en la dimensión del eje X WRT a la variable primaria de los problemas cuadráticos aleatorios generados (el número de restricciones del problema generado es la mitad del tamaño de su dimensión primaria). Para cada dimensión, el problema se genera en diferentes semillas, y los tiempos se obtienen como promedios sobre ejecuciones sucesivas para los mismos problemas. Este cuadro muestra para cada solucionador de referencia y un programa cuadrático aleatorio generado, los tiempos de placa, incluida la mediana (como DOT) y los valores mínimos y máximos obtenidos (definiendo la amplitud de la barra). Puede ver que ProXQP siempre está debajo de los solucionadores, lo que significa que es el más rápido para esta prueba.

Para problemas difíciles de la prueba de prueba Maros Meszaros, al solicitar una alta precisión (p. Ej., 1e-9), uno obtiene los resultados a continuación.

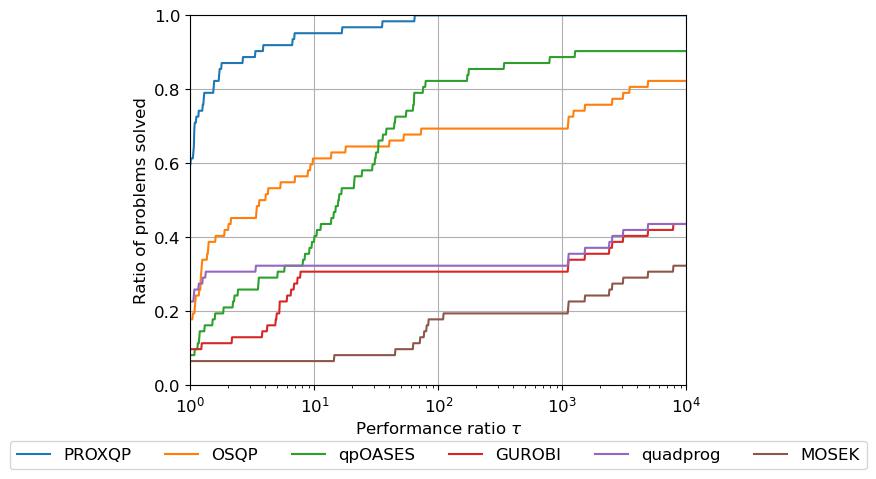
El cuadro anterior informa los perfiles de rendimiento de diferentes solucionadores. Es clásico para los solucionadores de evaluación comparativa. Los perfiles de rendimiento corresponden a la fracción de problemas resueltos (en el eje Y) en función de cierto tiempo de ejecución (en el eje X, medido en términos de un múltiplo del tiempo de ejecución del solucionador más rápido para ese problema). Entonces, cuanto más alto, mejor. Puede ver que ProXQP resuelve más rápido más del 60% de los problemas (es decir, para $ tau = 1 $ ) y que para resolver alrededor del 90% de los problemas, es como máximo 2 veces más lento que los solucionadores más rápidos que resuelven estos problemas (es decir, para $ tau aprox2 $ ).

Nota: Todos estos resultados se han obtenido con un núcleo Intel (R) de 11º generación (TM) i7-11850H @ 2.50GHz CPU.

Qplayer

Qplayer permite usar un QP como una capa dentro de las arquitecturas de aprendizaje estándar. Más precisamente, Qplayer se diferencia $ theta $ Las soluciones primarias y duales de QP de la forma

$$ begin {align} min_ {x} & ~ frac {1} {2} x^{t} h ( theta) x+g ( theta)^{t} x \ text {st} & ~ a ( theta) x = b ( theta) \ & ~ l ( theta) u ( theta) end {align} $$

dónde $ x in mathbb {r}^n $ es la variable de optimización. La función objetivo se define por una matriz semidefinita positiva $ H ( theta) in mathcal {s}^n _+$ y un vector $ g ( theta) in mathbb {r}^n $ . Las restricciones lineales se definen por la matriz de contratación de igualdad $ A ( theta) in mathbb {r}^{n_ text {eq} times n} $ y la matriz de restricción de desigualdad $ C ( theta) in mathbb {r}^{n_ text {in} times n} $ y los vectores $ b in mathbb {r}^{n_ text {eq}} $ , $ l ( theta) in mathbb {r}^{n_ text {in}} $ y $ u ( theta) in mathbb {r}^{n_ text {in}} $ de modo que $ b_i in mathbb {r}, ~ forall i = 1, ..., n_ text {eq} $ y $ l_i in mathbb {r} cup { - infty} $ y $ u_i in mathbb {r} cup { + infty}, ~ forall i = 1, ..., n_ text {in} $ .

Qplayer puede aprender más arquitecturas estructuradas. Por ejemplo, $ theta $ Can consiste solo en el aprendizaje de algunos elementos de $ A $ mientras deja $ B $ FIJO (ver por ejemplo, el ejemplo sobre cómo incluir Qplayer en una tubería de aprendizaje). Qplayer también puede diferenciar sobre LPS. Qplayer permite un cálculo paralelo sobre las CPU, y está interactuado con Pytorch .

Citando qplayer

Si está utilizando Qplayer para su trabajo, le recomendamos que cite el documento relacionado.

Procedimiento de instalación

Siga el procedimiento de instalación aquí.