GPU字體渲染
這是使用字體定義的向量大綱直接在GPU上渲染文本的演示。
字形的輪廓轉換為單個二次曲線曲線的列表(由其控制點定義),這些曲線已上傳到GPU。
為每個字形生成四邊形,然後像素著色器確定每個像素是內部還是外面的。為此,像素的繞組數是通過將射線與Bezzier曲線相交的。在每個交叉路口,射線要么進入或退出填充區域。在每個出口處,繞組數量都會增加一個,在每個入口時,繞組數量都會減少一個。考慮所有交叉點後,如果像素在輪廓內部,則繞組數將非零。
對於此繞組數量計算,射線的方向並不重要,但是通過使用與X軸平行的光線,可以大大簡化數學。通過從bezier曲線的控制點減去樣品位置,坐標係被移動,以使射線的起源在 $(0,0)$射線與正x軸一致。對於射線和偏斜曲線之間的交點 $ y = 0 $和 $ x ge 0 $必須是真實的。反疊縮(見下文)將沿射線的方向發生,但是可以通過首先旋轉圍繞原點的Bezier曲線的控制點來實現其他方向,從而使光線再次與X軸對準。
為了找到射線和單個bezier曲線之間的相交,請回想一下以下公式描述了二次曲線曲線(有關Bezier曲線的背景,請參見Beauty and Primer):
$$ textbf {c}(t)=(1-t)^2 textbf {p} _0 + 2(1-t)t textbf {p} _1 + t^2 textbf {p textbf {p} _2 $$
僅服用Y組件並應用條件 $ y = 0 $產生一個簡單的二次方程:
$$(1-t)^2 textrm {y} _0 + 2(1-t)t textrm {y} _1 + t^2 textrm {y} _2 = 0 $$
可以重新排列:
$$ textrm {y} _0 -2T textrm {y} _0 + t^2 textrm {y} _0 + 2t + 2t 2t textrm {y} _1-2T^2 2t^2 textrm {y}
$$( textrm {y} _0-2 2 textrm {y} _1 + \ textrm {y} _2)
因此,可以使用二次公式來解決它:
$$ t_ {0/1} = {-b pm sqrt {b^2-4Ac} vose 2a} $$
$$ a = textrm {y} _0-2 2 textrm {y} _1 + \ textrm {y} _2 _2 quad b = -2( textrm {y} _0 - textrm {y} _1)
替代 $ b = -2B $產量:
$ t t_ {0/1} = { - ( - 2B) pm sqrt {( - 2b)^2-4ac} over 2a} = {2b pm sqrt {4B^2-4AC} acta
$$ a = textrm {y} _0-2 2 textrm {y} _1 + textrm {y} _2 quad b = textrm {y} _0 - textrm {y} _1 quad C = textrm
二次方程可能具有一個或兩個解決方案。此外,一種解決方案 $ t $必須滿足 $ 0 le t< 1 $要在控制點描述的段上(不包括終點,因為它是輪廓下一個段的一部分)。最後,給定解決方案 $ t $相應的X坐標可以計算為 $ mathbf {c} _x(t)$檢查第二條件 $ x ge 0 $與十字路口。
在這一點上,已經確定了射線和Bezier曲線之間的相互作用,但仍需要將其分類為入口或退出。 Dobbie提供的演示明確計算了每個曲線的衍生物 $ t $這樣做的價值。但是,對於兩種潛在解 $ T_0/T_1 $ :
$ mathbf {c} _y(t)=( textrm {y} _0-2 2 textrm {y} _1 + textrm {y} _2 _2)t^2-2( textrm {y}
$$ mathbf {c} _y(t)= at^2-2b t + c $$
$$ frac {d mathbf {c} _y(t)} {dt} = 2at -2b $$
$ frac {d mathbf {c} _y(t_0)} {dt} = 2a {b - sqrt {b^2-ac} a}} - 2b = 2b = 2b -2b -2b -2 sqrt {b^2-ac} {b^2-ac} - 2-2-2-2-2-2-2-2-2-2-2-2-2-2b = -2 $ 0 0 $ 0 0 $ 0
$ frac {d mathbf {c} _y(t_1)} {dt} = 2a {b + sqrt {b^2-ac} a}} - 2b = 2b = 2b = 2b + 2 2 sqrt {b^2-ac} {b^2-ac} - 2-ac} - 2-ac} - 2b = 2 $}
因此,Bezier曲線在每個溶液處沿固定方向越過X軸,並與輪廓方向的慣例相結合, $ T_0 $永遠是出口 $ T_1 $總是條目。
理解這種關係的一種不同的方法是注意,由於解決方案中使用的不同符號,而平方根是非負的,所以 $ T_0 $必須先沿著曲線 $(t_0< = t_1)$如果 $ a> 0 $ 。相反,如果 $ a< 0 $ ,然後訂單被顛倒,然後 $ T_1 $必須先來 $(t_1< = t_0)$ 。參數 $ a $可以重寫為 $ 2( frac { textrm {y} _0 + textrm {y} _2}} {2} {2} - textrm {y} _1)$ ,因此其符號取決於第二個控制點是第一個控制點和第三個控制點的中點以上還是低於中點。下圖顯示,對於曲線方向的所有組合和參數的符號,該解決方案始終正確分類 $ a $ 。請注意沿曲線的解決方案的順序如何變化,但是射線總是進入 $ T_1 $解決方案並退出 $ T_0 $解決方案。
如果參數 $ a $是0(在浮點計算中足夠小),之間存在線性關係 $ t $和 $ y $ (這對於線性段是正確的,但對於某些非線性曲線也是如此),由於通過 $ a $ 。但是,由於關係現在是線性的,因此最多可以有一個解決方案,該解決方案很容易計算和分類。
沿射線方向進行抗氧化劑是通過考慮射線原點周圍像素大小的窗口來實現的。如果一個相交掉入此窗口,則僅分一分更改繞組數以計算像素的覆蓋範圍。分數重量取決於距像素左邊緣的距離(這與指向右側的射線是一致的)。通過考慮各個部分,可以看到這可以準確地計算一維覆蓋範圍。
請注意,我們還必須考慮現在稍後稍後稍後的射線起源,但是該實現首先計算與X軸的任何交集,然後驗證X位置,因此它不會改變太大。對此的另一種思考方式是條件 $ x ge 0 $表示為0的加權功能 $ x< 0 $和1 $ x ge 0 $ 。我們可以通過在一個像素的寬度上引入線性段來消除不連續性。
為了進行全面的抗氧化,我們可以沿著不同方向使用多個射線(例如沿X軸,沿Y軸沿X軸一個)。
筆記
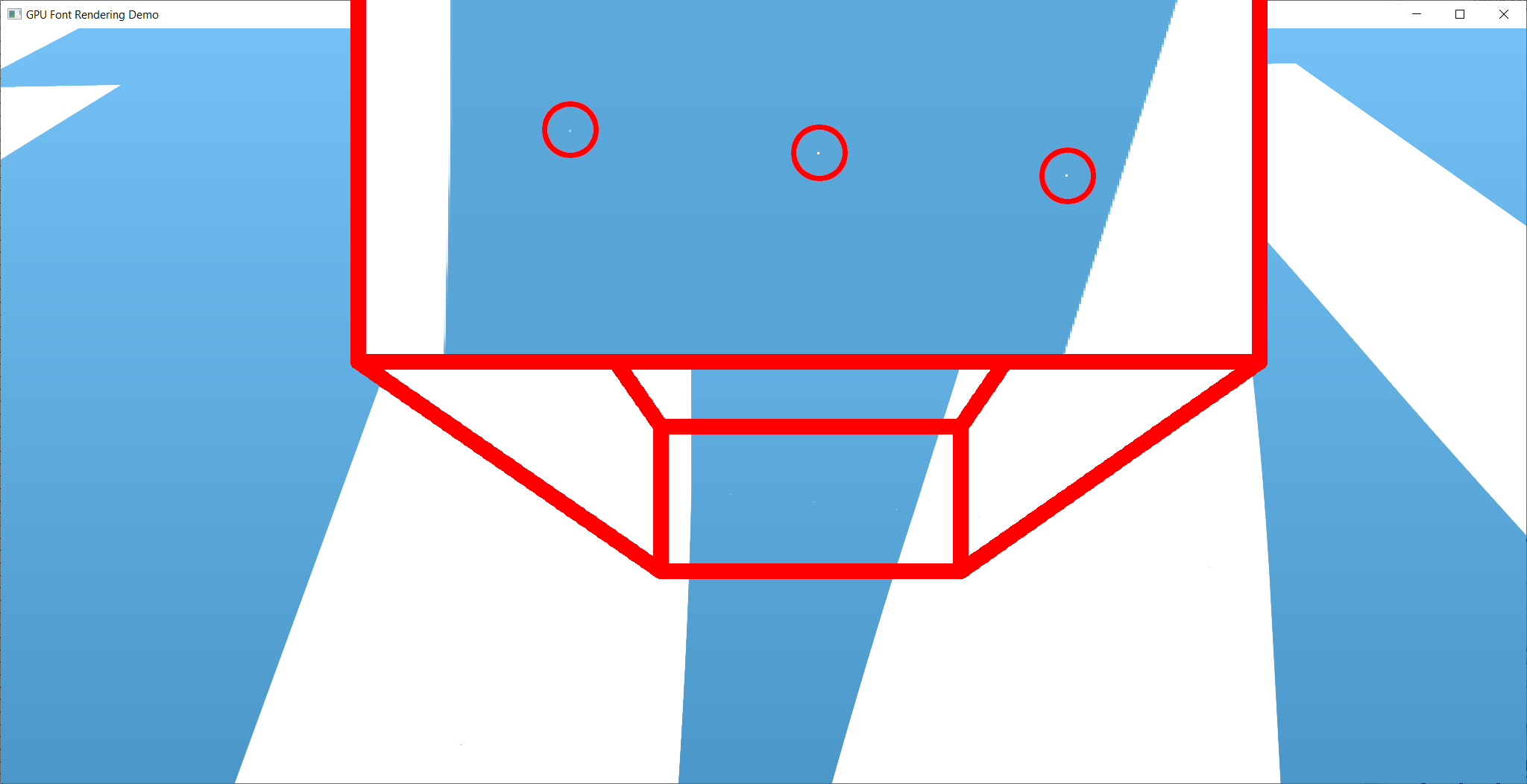
這種技術受到浮點數數量有限的數值精度的偽像。下圖顯示了完全放大(並知道在哪裡看)時的此類工件的實例。但是,我發現此實現已經在數字上已經非常穩定了。可以使用SLUG算法消除剩餘的任何偽像,由於相關專利,此處未實施。
該演示也不會實現任何性能優化(例如頻段),並且在某些情況下以及使用非常複雜的字體時可能具有很高的GPU使用情況。
建立說明
1。初始化sodules
將項目遞歸克隆,以初始化依賴項的子模型(或運行git submodule update --init如果您已經克隆了倉庫,請):
git clone --recursive https://github.com/GreenLightning/gpu-font-rendering.git
cd gpu-font-rendering
2。使用cmake
# Note: CMake will create the build directory.
cmake -S . -B build
make -j8 --directory build
在Windows上,您可能需要使用Cmake GUI和/或Visual Studio。
在Linux上,您可能必須安裝其他軟件包才能開發(例如,ubuntu sudo apt-get install xorg-dev libgl1-mesa-dev )。
3。從主要項目目錄運行
該程序要求fonts和shaders目錄在當前目錄中以加載其資源。如果您只得到黑色窗口,那麼這很可能是問題。檢查您的工作目錄並檢查控制台是否錯誤。
在Windows 10,Macos Monterey和Ubuntu 22.04上進行了測試。
